Akademik

выпуклая оболочка конечного числа точек в евклидовом пространстве Eⁿ. Такой В. м. есть ограниченное непустое пересечение конечного числа замкнутых полупространств. Бесконечным В. м. называют пересечение конечного числа замкнутых полупространств, содержащее по крайней мере один луч, причем уславливаются пространство 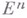также считать В. м. В этом смысле В. м. есть замкнутая выпуклая оболочка конечного числа точек и лучей. Размерностью В. м. наз. минимальную размерность содержащего его пространства

В. м. - частный вид выпуклого множества. Как пересечение полупространств В. м. описывается системой линейных неравенств и может быть исследован алгебраическими средствами. Методы минимизации линейных форм на В. м. составляют предмет линейного программирования.

В. м. имеет конечное число граней (пересечений В. м. с опорными гиперплоскостями). Каждая грань В. м. есть В. м. меньшей размерности. Грани граней являются гранями исходного В. м. Одномерные грани наз. ребрами, нульмерные - вершинами. Ограниченный В. м. есть выпуклая оболочка своих вершин.

В теории выпуклых поверхностей В. м. наз. также границу В. м., а иногда (см. [1]) даже часть такой границы. В последнем случае говорят о выпуклом многограннике с краем. В элементарной геометрии принято первоначально определять многогранник как фигуру, специальным образом составленную из многоугольников (см. [2]), а затем выделять В. м. как лежащий по одну сторону от плоскости каждой его грани.

Ограниченный n-мерный В. м. имеет не менее чем вершину. Наиболее просто устроен симплекс, имеющий вершину. Всякий ограниченный В. м. разбивается на симплексы, прилегающие по целым граням.

В евклидовом пространстве есть пять правильных В. м.: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Об их свойствах и аналогах см. Правильные многогранники, Полуправильные многогранники, О В. м. с частными особенностями строения см. Изогоны и изоэдры, Зоноэдры. С правильными разбиениями пространства связаны специальные типы В. м.: стереоэдры, параллелоэдры, планигоны.

Возможные типы строения сети граней В. м. изучены не полностью. Пусть - число k-мерных граней ограниченного га-мерного В. м. Справедливо соотношение Эйлера

имеющее топологич. характер: оно верно для любого разбиения сферы 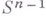на простые ячейки. При для не образующей двуугольных и самокасающихся ячеек связной сети ребер на сфере найдется В. м. в евклидовом пространстве с таким строением сети (теорема Штейница). При строение сети граней В. м. менее произвольно, чем возможные разбиения сферы (см. [3]). В классе В. м. могут ставиться специфические экстремальные задачи, в условия к-рых входят строение сети граней, число или суммарная длина ребер и т. п. (см. [4]).

Приближение выпуклых тел посредством В. м. является универсальным приемом исследования. Приближением В. м. получены многие результаты теории смешанных объемов, теоремы существования, единственности, устойчивости выпуклых поверхностей с фиксированными данными, развиты геометрич. методы решения Монжа - Ампера уравнения. Эффективность этого метода связана с тем, что В. м. характеризуются конечным числом данных; для В. м. общие теоремы имеют простую формулировку; к В. м. применимы синтетич. приемы исследования.

В связи с теорией поверхностей сформировался большой раздел теории В. м. (см. [1]). В евклидовом пространстве Е ³ два ограниченных В. м., имеющие одинаковые и в одинаковом порядке прилегающие грани, совместимы движением (теорема Коши). В Е ⁿ для нек-рых 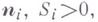удовлетворяющих соотношению

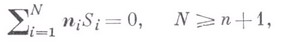
существует и единствен с точностью до переноса В. м. с единичными внешними нормалями 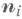граней и площадями граней (теорема Минковского). Развертка из плоских многоугольников, склеиваемая так, что результат гомеоморфен сфере и вокруг каждой вершины склеиваются углы с суммой , изометрич-на В. м. в , и этот В. м. единствен с точностью до движения (теорема А. Д. Александрова). Два В. м. в совместимы переносом, если ни для одного направления нормали 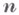грань Одного В. м. нельзя переносом сделать строгой частью другого. Для выходящих из точки лучей 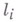и чисел существует и единствен с точностью до гомотетии В. м. с вершинами на лучах и кривизнами 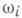в этих вершинах.

Лит.: [1] Александров А. Д., Выпуклые многогранники, М.-Л., 1950; [2] Тот Л. Ф., Расположения на плоскости, на сфере и в пространстве, пер. с нем., М., 1958; [3] Энциклопедия элементарной математики, кн. 4, Геометрия, М., 1963; [4] Convex polytopes, L.-N.Y.- Sydney, 1967. В. А. Залгаллер.