Akademik

в специальной теории относительности - преобразования координат и времени к.-л. события при переходе от одной инерциалъной системы отсчёта (и. с. о.) к другой; выражают равноправие всех и. с. о. в описании законов природы. Впервые Л. п. были сформулированы в 1904 в связи с теоретич. и эксперим. работами по исследованию распространения света. Было установлено, что Максвелла уравнения сохраняют свою форму при Л. п. и, с другой стороны, Л. п. могут быть выведены как следствие (эксперим. факта) одинаковости скорости света в вакууме относительно произвольной системы отсчёта. В дальнейшем было осознано, что Л. п. имеют универсальный характер, являются матем. реализацией относительности принципами тем самым отражают общие свойства пространства и времени. Решающий шаг в этом направлении был сделан А. Эйнштейном (A. Einstein), важнейшую роль сыграли труды X. А. Лоренца, А. Пуанкаре (A. Poincare), Г. Минков-ского (Н. Minkowski).

Если и. с. о. К' движется относительно и. с. о. К с пост. скоростью V вдоль оси х, то Л. п. имеют вид

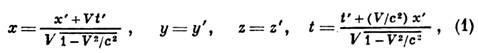
где с - скорость света в вакууме. Ф-лы, выражающие 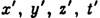через х, у, z, t, получаются из (1) заменой V на -V. В случае медленных движений ( 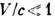) преобразования (1) приближённо переходят в преобразования Галилея:

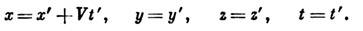
Л. и. (1) не совместимы с классич. (дорелятивистскими) представлениями о пространстве и времени. В классич. физике принимается, что понятие одновременности событий и, в частности, промежуток времени между двумя событиями (напр., между актами рождения и распада нестабильной частицы) имеют абс. смысл, т. е. они не зависят от движения наблюдателя. Как установлено относительности теорией, промежутки времени и отрезки длины [в соответствии с (1)] зависят от движения системы отсчёта. Они относительны примерно в том же смысле, в каком относительными (зависящими от расположения наблюдателей) являются суждения наблюдателей об угл. расстоянии, под к-рыми они видят одну и ту же пару предметов.

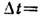
Если в системе К' два события, происходящие в одном и том же месте, разделены промежутком времени dt', то в системе К эти же события (происходящие в разных местах) разделены промежутком времени 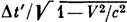. Одна из эксперим. проверок этого вывода состоит в наблюдении за частицами (напр., мюонами), способными к самопроизвольному распаду. Время жизни покоящихся (или движущихся с малыми скоростями) мюонов 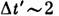мкс. Мюоны же, образующиеся в потоке космических лучей, движутся относительно Земли со скоростями, достигающими 0,995 с, и успевают пролететь, не распадаясь, ок. 6 км, т. е. их время жизни с точки зрения земного наблюдателя в 10 раз больше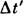

Аналогично, если отрезок покоится в системе К' и имеет длину 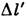, то его длина 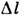в системе K, т. в. расстояние между двумя одновременными в К событиями регистрации положения концов отрезка, принимает значение 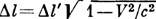. Этот результат наз. лоренцевым сокращением д. лины. Так же изменяется объём тела, поскольку преобразуется только продольный (вдоль движения) размер тела, а поперечные размеры не изменяются.

Из Л. п. (1) вытекают ф-лы преобразования скоростей:

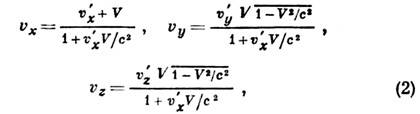
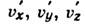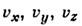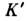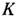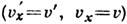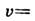
где и - компоненты скорости объекта соответственно в системах и . В частности, для частицы, движущейся вдоль оси х,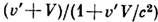. Отсюда следует, что для частицы, движущейся с досветовой скоростью, 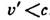, всегда (в любой системе отсчёта)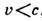, а скорость частицы, движущейся со скоростью света, 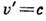, всегда равна с, 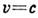. Ф-лы (1) не имеют смысла при 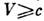, что соответствует невозможности движения материальных тел со скоростью, превышающей или равной скорости света.

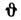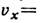
Исходя из преобразований (2), можно получить формулу Для релятивистской аберрации света. Если луч света распространяется в системе К под углом ( 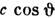, , 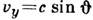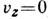), то относительно системы 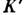он распространяется под углом 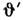, связанным с 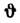формулой

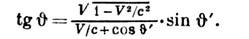
При 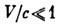для угла аберрации 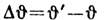получается обычная зависимость: Ф-лы (1) указывают на относительность промежутков времени и отрезков длины между событиями, однако оставляют инвариантной (не зависящей от выбора системы отсчёта) их комбинацию, наз. интервалом(s). Квадрат интервала между событиями равен:

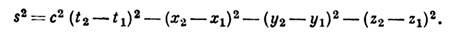
Для бесконечно близких событий интервал ds между ними определяется равенством

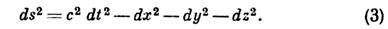
Величина 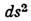имеет смысл квадрата элемента длины в четырёхмерном мире (мире Минковского), объединяющем пространство и время в неразрывное целое - пространство-время (см. Минковского пространство-время). Объединение пространственных и временного измерений не означает их тождественности. Физ. различие между ними выражается тем, что 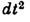входит в (3) с др. знаком.

Геометрически преобразования (1) можно рассматривать как поворот четырёхмерной системы координат t, x, у, z в плоскости 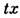. Три преобразования, подобные (1) (по числу трёх возможных поворотов в плоскостях tx, ty, dz), вместе с тремя пространств. поворотами и четырьмя постоянными сдвигами начала координат (по осям t, x, у, z )образуют 10-параметрич. группу преобразований, называемую Пуанкаре группой. Это наиб. широкая группа непрерывных преобразований, оставляющих форму (3) неизменной. Три Л. п. вместе с тремя пространств. поворотами образуют 6-параметрич. Лоренца группу. Но сами Л. п. не образуют группу, т. к. три последоват. Л. п. могут привести к и. с. о., неподвижной по отношению к исходной, но отличающейся пространств. поворотом (т. н. томасовская прецессия).

Различные физ. величины преобразуются под действием Л. п. в зависимости от их свойств ковариантности. Наиб. употребительными являются четырёхмерные скаляры, векторы, тензоры, спиноры. Примером (антисимметричного) тензора второго ранга является тензор эл.-магн. поля, элементы к-рого представляют собой пространств. компоненты напряжённостей электрич. Е и магн. Н полей. Под действием Л. п. Е и H преобразуются след. образом:

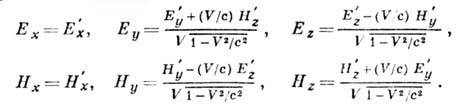
Т. о., чисто электрич. или чисто магн. поле в одной системе отсчёта может обладать соответственно магн. или электрич. компонентами в другой.

Как отмечалось, ур-ния Максвелла инвариантны относительно Л. п. (нештрихованные величины лишь заменяются штрихованными или наоборот). Приведение ур-ний механики к виду, инвариантному относительно Л. п., потребовало уточнения понятий энергии и импульса. Энергия тела (частицы) 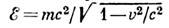и его импульс 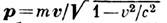[где т - масса (масса покоя) тела] объединяются в 4-вектор энергии-импульса с компонентами 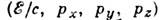. Под действием (1) они преобразуются след. образом:

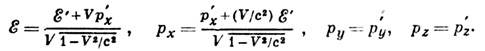
Квадрат 4-вектора энергии-импульса является инвариантом:

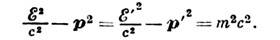
Для частиц, движущихся со скоростью света, он, очевидно, равен нулю.

Л. п. играет важную роль не только в классич. (неквантовой), но и в квантовой физике. Под действием Л. п. преобразуются волновые ф-ции ( векторы состояния )квантовой системы, удовлетворяющие соответствующим ур-ниям движения, обеспечивая их инвариантность.

Лит.: Ландау Л. Д., Лифшиц Е. М., Теория поля, 7 изд., М., 1988; Принцип относительности, [Сб. ст.], М., 1973; Медведев Б. В., Начала теоретической физики, М., 1977. Л. П. Грищук.