Akademik

(количество движения) - в нерелятнви стекой механике Ньютона - мера механич. движения, представляющая собой векторную величину, равную для материальной точки произведению массы m этой точки на её скорость v и направленную так же, как вектор скорости: p=mv. И. точки остаётся постоянным только при отсутствии сил. Под действием силы F И. точки изменяется в общем случае и по численной величине, и по направлению; характер этого изменения определяется ур-нием dp/dt=F, выражающим основной закон механики, с помощью к-рого решаются все задачи динамики точки. И. механич. системы наз. величина P, равная гл. вектору (геометрич. сумме) И. всех точек системы или произведению массы М всей системы на скорость v_c её центра масс: 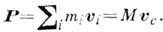Изменение И. системы может происходить только в результате внешних воздействий, т. е. под действием внешних сил F^e_{i .} Для замкнутой системы, т. е. системы, не испытывающей никаких внешних воздействий, имеет место закон сохранения И. Величина И. Р такой системы остаётсявекторно постоянной, хотя И. отд. частой Системы могут в результате их взаимодействий изменяться. Этот закон объясняет реактивное движение, отдачу (или откат) при выстреле, работу гребного винта и др. И. обладают все формы материи, в т. ч. эл.-магнитн., гравитац. и др. поля (см. Поля физические). В классич. механике более распространён термин "количество движения", в то время как в релятивистской и квантовой механике, квантовой теории поля обычно применяется термин "И.". с. М. Тарг. Полный И. среды (поля) равен геом. сумме произведения векторов плотности И. элементарных объёмов на эти объёмы (в пределе оно равно соответствующему объёмному интегралу). Для полей векторы И. и его плотности выражаются через величины напряжённостей, потенциалов и т. п. Напр., вектор плотности И. эл.-магн. поля равен [ЕН]/4p с, где E - электрич., а Н - магнитная напряжённости поля. Наличие И. у эл.-магн. поля проявляется, напр., в световом давлении. И. фотона (впервые введённый А. Эйнштейном в его теории фотоэффекта) частоты v= w/2p равен 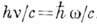, где 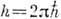. В квантовой механике часто пользуются И. в качестве независимой переменной волновой ф-ции, т. е. выбирают волновую ф-цию в импульсном представлении. В релятивистской механике Эйнштейна И. свободной частицы массы m связан со скоростью v соотношением 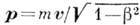, где b=v/c. В четырёхмерном Минковского пространстве-времени совокупность компонент И. ( р _х, р _у, р _z )и величина iE/c (где 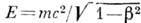- энергия частицы) составляют четырёхмерный вектор р _i, где р ₁ р ₂, р ₃ - компоненты И. частицы, a p₄=iE/c. Четырёхвектор И. р _i связан со скоростью четырёхмерной u_i ф-лой р _i=mcu_i. Если воспользоваться соотношением и ²_i=-1, то можно получить связь между энергией и И. частицы E²/с ²=р ²+m² с ². Энергия, И. и скорость свободной частицы связаны соотношением p=Ev/c². Выражения для И. и энергии при v=c обращаются в бесконечность (если масса отлична от нуля). Т. о., частицы с ненулевой массой могут двигаться лишь со скоростью меньшей, чем скорость света. Выражение для И. при скоростях, много меньших скорости света, переходит в обычное классич. выражение (в отличие от энергии, к-рая принимает значение тс ²+тv²/2). При переходе к др. инерциалъной системе отсчёта импульс преобразуется согласно Лоренца преобразованиям. По спец. относительности теории взаимодействия распространяются с конечной скоростью, не превышающей скорости света в вакууме, т. е. И., излучённый одной частицей, не может мгновенно передаваться др. частицам. Суммарный И. всех частиц не может, следовательно, сохраняться. Закон сохранения И., однако, имеет место и в этом случае, если учесть И., присущий полю - носителю взаимодействий, к-рому приписывают плотность И. и плотность потока И. В квантовой механике и квантовой теории полей сказанное выше справедливо по отношению к ср. значениям соответствующих операторов. Сохранение И. есть следствие однородности пространства; этим объясняется подчинение весьма разл. явлений одному и тому же закону (см. Сохранения законы). В. В. Судаков.