- ПЕРЕМЕННЫЙ ТОК
-
в широком смысле электрический ток, изменяющийся во времени. П. т. создаётся перем. напряжением. В технике обычно под П. т. понимают периодич, ток, в к-ром средние за период значения силы тока и напряжения равны нулю. Периодом Т П. т. наз. наименьший промежуток времени (в с), через к-рый значения силы тока (и напряжения) повторяются (рис. 1). Важной хар-кой П. т. явл. его частота f — число периодов в 1 с: f=1/T. В СССР стандартная техн. частота f=50 Гц.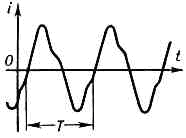
Рис. 1. График периодич. перем. тока i(t).Для передачи и распределения электрич. энергии преим. используется П. т. (благодаря простоте трансформации его напряжения почти без потерь мощности). П. т. может быть выпрямлен, напр. ПП выпрямителем, а затем с помощью ПП инверторов преобразован вновь в П. т. другой, регулируемой частоты; это создаёт возможность использовать простые и дешёвые двигатели П. т. (асинхронные и синхронные) для электроприводов, требующих плавного регулирования скорости. Генераторы и двигатели П. т. по сравнению с машинами постоянного тока при равной мощности проще по устройству, дешевле и надёжнее.Для хар-ки силы П. т. за основу принято сопоставление ср. теплового действия П. т. с тепловым действием пост. тока соответствующей силы. Полученное таким путём значение силы I П. т. наз. действующим (или эффективным) значением, математически представляющим среднеквадратичное за период значение силы тока. Аналогично определяется и действующее значение напряжения U П. т. Амперметры и вольтметры П. т. измеряют именно действующие значения тока и напряжения.В простейшем и наиб. важном случае мгновенное значение силы i П. т. меняется во времени t по синусоидальному закону: i=Imsin(wt+a), где Im— амплитуда тока, w=2pf — его круговая частота, a — нач. фаза. Синусоидальный (гармонический) ток создаётся синусоидальным напряжением u той же частоты: u=Umsin(wt+b), где Um— амплитуда напряжения, b— нач. фаза (рис. 2).
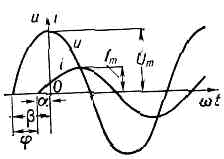Рис. 2. Графики напряжения U и тока i в цепи перем. тока при сдвиге фаз j.Действующие значения такого П. т. равны: I=Im?2»0,707 1m, U=Uт/?2»0,707Um. Для синусоидальных токов, удовлетворяющих условиям квазистационарности (см. КВАЗИСТАЦИОНАРНЫЙ ТОК); в дальнейшем будут рассматриваться только такие токи), справедлив Ома закон (закон Ома в дифф. форме справедлив и для неквазистационарных токов в линейных цепях). Из-за наличия в цепи П. т. индуктивности L или (и) ёмкости С между током i и напряжением и в общем случае возникает сдвиг фаз j=b-a, зависящий от параметров цепи (r, L, С, где r — активное сопротивление) и частоты w.
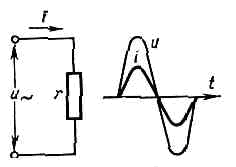Рис. 3. Схема цепи и графики напряжения и U тока i в цепи, содержащей только активное сопротивление r.Вследствие сдвига фаз ср. мощность Р. П. т., измеряемая ваттметром, меньше произведения действующих значений тока и напряжения: Р=IUcosj.В цепи, не содержащей ни индуктивности, ни ёмкости, ток совпадает по фазе с напряжением (рис. 3). Закон Ома для действующих значений этой цепи имеет такую же форму, как и для цепи пост. тока: I=U/r. Активное сопротивление цепи r определяется по активной мощности Р, затрачиваемой в цепи: r=Р/I2.При наличии в цепи индуктивности L П. т. индуцирует в ней эдс самоиндукции eL=-Ldi/dt=-wLImXXcos(wt+a)=wLImsin(wt+a-p/2).Эдс самоиндукции противодействует изменению тока, и в цепи, содержащей только индуктивность, ток отстаёт по фазе от напряжения на четверть периода, т. е. j=p/2 (рис. 4). Действующее значение eL равно: ?L=IwL=IxL, где xL=wL — индуктивное сопротивление цепи. Закон Ома для такой цепи имеет вид: I=U/XL=U/wL.
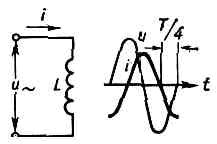Рис. 4. Схема цепи и графики напряжения U и тока i в цепи, содержащей только индуктивность L.При напряжении и на конденсаторе ёмкости С заряд на его обкладках будет равен q=Cu. Периодические изменения и вызывают периодическое изменение q, и возникает ёмкостный ток:i=dq/dt=C•du/dt=wCUmXcos(wt+b)=wCUmsin(wt+b+p/2). Т. о., синусоидальный П. т., проходящий через ёмкость, опережает по фазе напряжение на её зажимах на четверть периода, т. е. j=-p/2 (рис. 5). Эфф. значения в такой цепи связаны соотношением I=wCU=U/xc, где xс=1/wС — ё м к о с т н о е сопротивление цепи.Если цепь П. т. состоит из последовательно соединённых r, L и С, то её п о л н о е сопротивление равно: z=?(r2+x2), где х=xL-xc=wL — -1/wС — реактивное сопротивление цепи П. т.
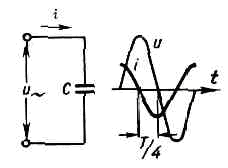Рис. 5. Схема цепи и графики напряжения U и тока i в цепи, содержащей только ёмкость С.Соответственно закон Ома имеет вид: I=U/z= U/?(r2+(wL-1/wC)2), а сдвиг фаз между током и напряжением определяется отношением реактивного сопротивления к активному: tgj=x/r. В такой цепи при совпадении частоты вынужденных колебаний, создаваемых источником П. т., с резонансной частотой w0=l/?LC индуктивное и ёмкостное сопротивления равны (wL=l/wC) и полностью компенсируют друг друга, сила тока максимальна и наблюдается явление резонанса (см. КОЛЕБАТЕЛЬНЫЙ КОНТУР). В условиях резонанса напряжения на индуктивности и ёмкости могут значительно (часто во много раз) превышать напряжение на зажимах цепи.Для расчётов разветвлённой цепи П. т. используют Кирхгофа правила. Несинусоидальность П. т. в электроэнергетич. системах обычно нежелательна, и принимаются спец. меры для её подавления. Но в цепях электросвязи, в полупроводниковых и электронных устройствах несинусоидальность создаётся самим рабочим процессом. Если среднее за период значение тока не равно нулю, то он содержит постоянную составляющую. Для анализа процессов в цепях несинусоидального тока его представляют в виде суммы простых гармонич. составляющих, частоты к-рых равны целым кратным числам осн. частоты: i=I0+Ilmsin(wt+a1)+I2mXsin(2wt +a2)+...+Ikmsin(kwt+ak). Здесь I0 — постоянная составляющая тока, I1msin(wt+a1) — первая гармонич. составляющая (осн. гармоника), остальные члены — высшие гармоники. Расчёт линейных цепей несинусоидального тока на основе принципа суперпозиции ведётся для каждой составляющей (т. к. хL и xc зависят от частоты). Алгебр. сложение результатов таких расчётов даёт мгновенное значение силы (или напряжения) несинусоидального тока.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ПЕРЕМЕННЫЙ ТОК
-
- электрическийток, изменяющийся во времени. В общем понимании к П. т. относят разл. виды импульсных, пульсирующих, периодич. и квазипериодич. токов. В техникепод П. т. обычно подразумевают периодич. или почти перподич. токи перем. направления. Наиб. употребителен П. т., сила к-рого J меняется вовремени по гармонич. закону (гармонический, или синусоидальный, П. т.):
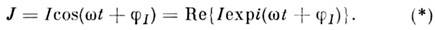
Здесь I - амплитуда,
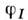- нач. фаза,
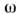- круговая частота. В эл.-технике (и, частично, в радиотехнике) обычнореализуются квазистационарные цепи . П. т. [см. Квазистационарное (квазистатическое)приближение]. При этом в многопроводных системах, предназначенныхдля передачи энергии, часто используют многофазные П. т. - текущие по разнымпроводам токи с одинаковыми амплитудами, но разными фазами. В частности, в симметричных трёхфазных системах фазы отличаются на 2
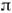/3.Большинство пассивных электрич. цепей работает в линейном режиме, когдасправедлив суперпозиции принцип. При прохождении через такие цепичисто гармонич. П. т. (*) не искажают своей формы, тогда как при наличиинелинейных элементов (напр., железных сердечников в трансформаторах, нелинейныхпреобразователей, диодов, триодов и т. п.) синусоидальные сигналы искажаются, обогащаясь высшими гармониками. Квазистационарные цепи с сосредоточеннымипараметрами могут быть составлены как определ. комбинации индуктивностей L,ёмкостей С и сопротивлений R. Связь между напряжением . и силой П. т. J в этих элементах задаётся ф-лами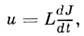 
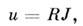
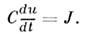
В нелинейных режимах величины L, С,R являются ф-циями протекающего тока J; в линейных режимах онилибо постоянны, либо зависят в явном виде от времени (параметрич. системы).
При расчёте электрич. цепей гармонич. П. т. удобно пользоваться комплексными амплитудами напряжения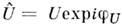
(U- амплитуда напряжения) и тока 
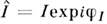и комплексными импедансами
принимающими на индуктивных, ёмкостныхи резистивных участках соответственно значения ZL=
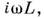
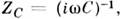ZR= R. Тогда квазистационарная линейная цепь (многополюсник) любой сложностидопускает расчёт по обычным Кирхгофа правилам. Так, для последовательнавключённых элементов L, С, R суммарный импеданс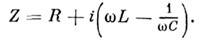 
Это импеданс колебательного Z/СЛ-контура, высокодобротного при условии L/CR
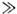1.На резонансной (томсоновской) частоте 
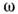= ( ЬС)~1/* импеданс Z минимален но модулю. Методкомплексных амплитуд порождает метод векторных (круговых) диаграмм, основанныйна графит, построении напряжений и токов как векторов на комплексных плоскостях, что придаст наглядность решениям мн. задач эл.-техники.
Мощность W, выделяемая в цепи П. т., определяется усреднением за период колебаний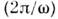
произведения и J: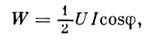
где
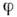- разность фаз между напряжением и током. Иногда вводят понятие эффективных(действующих) напряжений 
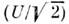и токов 
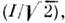чтобы ф-ла для оптимально поглощаемой (отдаваемой сопротивлению) мощностиимела тот же вид, что и для цепей пост. тока. Этот оптимум достигаетсяпри значении 
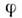=0. Такой режим наз. согласованным. При 
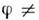0часть мощности "отражается" обратно к источнику. Поэтому иногда проблемусогласования в эл.-технике наз. проблемой "оптимального cos
".
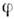С ростом частоты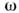
квазистационарное приближение перестаёт быть справедливым, и для полученияраспределения П. т. необходимо обращаться непосредственно к Максвеллауравнениям. Чтобы подчеркнуть это обстоятельство, иногда такие токиназ. быстропеременными (БПТ) и предпочитают оперировать не с суммарными(интегральными) силами тока, а с их объёмными плотностями j(r,t). Припротекании по хорошо проводящим телам БПТ стремятся прижаться к их наружнымповерхностям (скин-эффект). В случае идеальной проводимости они распределяютсяпо самой поверхности; такие токи наз. поверхностными и характеризуютсяповерхностными плотностями. Плотность БПТ всегда можно разбить на потенциальнуюи вихревую компоненты. Последняя ответственна за возбуждение вихревых эл.-магн. полей. В открытых (неэкранированных) системах именно с вихревыми П. т. связано излучение эл.-магн. энергии. Это, в частности, используется в излучателях(антеннах), где путём подбора надлежащих распределений БПТ создаются требуемыеугл. распределения полей излучения (диаграммы направленности).Лит.: Нелинейные электрические цепи. Электромагнитное поле, 4 изд., М., 1979; Касаткин А. С., Немцов М. В.,Электротехника, 4 изд., М., 1983; Поливанов К. М., Линейные электрическиецепи с сосредоточенными постоянными, М., 1972.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.