Akademik

СВЯЗИ МЕХАНИЧЕСКИЕ

СВЯЗИ МЕХАНИЧЕСКИЕ: ограничения, налагаемые на положение или движения механич. системы. Обычно С. м. осуществляются с помощью к.-н. тел. Примеры таких С. м.— поверхность, по к-рой скользит или катится тело; нить, на к-рой подвешен груз; шарниры, соединяющие звенья механизмов, и т. п. Если положения точек механич. системы по отношению к данной системе отсчёта определять их декартовыми координатами хk,yk, zk (k=1, 2, . . ., n, где n — число точек системы), то ограничения, налагаемые С. м., могут быть выражены в виде равенств (или неравенств), связывающих координаты xk, yk, zk, их первые производные по времени x.k,y.k,z.k (т. e. скорости точек системы) и время t.

С. м., налагающие ограничения только на положения (координаты) точек системы и выражающиеся ур-ниями вида

f(...,xk, yk, zk, t)=0, (1)

наз. геометрическими. Если же С. м. налагают ограничения ещё и на скорости точек системы, то они наз. кинематическими, а их ур-ния имеют вид: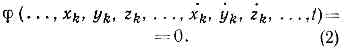

Когда ур-ние (2) может быть проинтегрировано по времени, соответствующая кинематич. связь наз. интегрируемой и эквивалентна геом. связи. Геом. и интегрируемые кинематич. связи носят общее назв. г о л о н о м н ы х С. м. (см. ГОЛОНОМНЫЕ СИСТЕМЫ). Кинематич. неинтегрируемые С. м. наз. н е г о л о н о м н ы м и (см. НЕГОЛОНОМНЫЕ СИСТЕМЫ).

С. м., не изменяющиеся со временем, наз. стационарными (их ур-ния не содержат явно время t), а С. м., изменяющиеся со временем, наз. нестационарными. Наконец, С. м., при к-рых каждому возможному перемещению точек системы соответствует перемещение прямо противоположное по направлению, наз. удерживающими (их ур-ния выражаются равенствами вида (1), (2)), а С. м., не удовлетворяющие этому условию (напр., гибкая нить, допускающая перемещение вдоль нити только в одном направлении), наз. неудерживающими и их ур-ния выражаются неравенством вида f(. . ., xk, yk, zk, . . .)?0.

Методы решения задач механики существенно зависят от характера С. м., налагаемых на систему. Эффект действия С. м. можно учитывать введением соответствующих сил, наз. реакциями связей; при этом для определения реакций (или для их исключения) к ур-ниям равновесия или движения системы должны присоединяться ур-ния связей вида (1) или (2). С. м., для к-рых сумма элементарных работ всех реакций на любом возможном перемещении системы равна нулю, наз. идеальными (напр., лишённая трения поверхность или гибкая нить). Для механич. систем с идеальными С. м. можно сразу получить ур-ния равновесия или движения, не содержащие реакций связей, используя (см. ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ ПРИНЦИП, Д'АЛАМБЕРА — ЛАГРАНЖА ПРИНЦИП, ЛАГРАНЖА УРАВНЕНИЯ).

СВЯЗИ МЕХАНИЧЕСКИЕ

- ограничения, к-рые налагаются на положенияи скорости точек механич. системы и выполняются независимо от того, какиезаданные силы действуют на систему. Обычно С. м. осуществляются с помощьюк.-н. тел. Примеры таких С. м.: поверхность, по к-рой скользит или катитсятело; нить, на к-рой подвешен груз; шарниры, соединяющие звенья механизмов, и т. п. Если положения точек механич. системы по отношению к данной системеотсчёта определять их декартовыми координатами 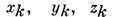(k =1, 2,..., n, где п - число точек системы), то ограничения, налагаемые С. м., могут быть выражены в виде равенств (или неравенств),связывающих координаты 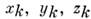, их первые производные по времени 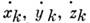(т. е. скорости точек системы) и время t. С. м., налагающие ограничениятолько на положения (координаты) точек системы и выражающиеся ур-ниямивида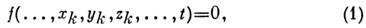

наз. геометрическими. Если же С. м. налагают ограничения ещё и на скороститочек системы, то они наз. кинематическими или дифференциальными, а ихур-ния имеют вид:

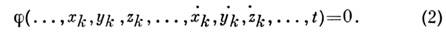
Когда ур-ние (2) может быть проинтегрировано по времени, соответствующаякинематич. связь наз. и н-тегрируемой и эквивалентна геом. связи. Геом. и интегрируемые кинематич. связи носят общее название г о л о н о м н ых С. м. (см. Голономная система). Кинематич. неинтегрируемые С. м. наз. н е г о л о н о м н ы м и (см. Неголономная система).

С. м., не изменяющиеся со временем, наз. стационарными [ур-ния (1) или(2) для таких С. м. время t явно не содержат]; С. м., изменяющиесясо временем [как в ур-ниях (1) и (2)], наз. нестационарными. Наконец, когдаограничения, налагаемые С. м., сохраняются при любом положении системы, эти С. м. наз. удерживающими и выражаются ур-ниями вида (1) или (2). Еслиже С. м. указанными свойствами не обладают и точки системы могут от такихсвязей «освобождаться» (напр., груз, подвешенный на нити), то такие С. м. наз. неудерживающими 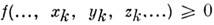и выражаются неравенствами вида.

Методы решения задач механики существенно зависят от характера С. м.,наложенных на систему. Эффект действия С. м. можно учитывать введениемсоответствующих сил, наз. реакциями связей; при этом для определенияреакций (или для их исключения) к ур-ниям равновесия или движения системыдолжны присоединяться ур-ния связей вида (1) или (2). С. м., для к-рыхсумма элементарных работ всех реакций связей на любом возможном перемещениисистемы равна нулю, наз. идеальными (напр., лишённая трения поверхностьили гибкая нить). Для механич. систем с идеальными С. м. можно сразу получитьур-ния равновесия или движения, не содержащие реакций связей, используя возможных перемещений принцип, Д'Аламбера - Лагранжа принцип или Лагранжа уравнения механики.

Лит. см. при ст. Механика, Динамика. С. М. Тарг.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.