Akademik

- мультипольный момент 2-го порядка (ранга), характеризующий источники к.-л. поля. Напр., К. м. системы электрич. зарядов, распределённых в объёме V с плотностью r(r), наз. симметричный тензор
,
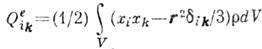где x_i, x_k - компоненты вектора r, d_ik - символ Кронекера. (Используются и др. нормировки К. м., отличающиеся от приведённой коэф. 3 или 6.) Поскольку след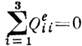 , то в общем случае имеется всего 5 независимых составляющих электрич. К. м.; из них собственно К. м. иногда наз. только диагональную составляющую 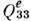. Если электрич. дипольный момент р ^е и суммарный заряд q системы равны нулю, то тензор электрич. К. м. не зависит от выбора начала отсчёта (точки r=0). Потенциал эл.-статич. поля стационарной системы зарядов на расстояниях R,больших по сравнению с её размерами l, R д l, с учётом первых трёх мультиполей имеет вид 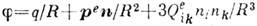(здесь и далее по повторяющимся индексам i и k производится суммирование). В этой ф-ле использована Гаусса система единиц, вектор n=R/R задаёт направление от системы (r=0) в точку наблюдения R.Квадрупольную составляющую потенциала можно представить как поле сосредоточенного (точечного, l "0)электрического К. м., отвечающего распределению зарядов, где
-
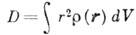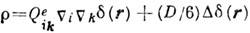
среднеквадратичный радиус исходного распределения плотности заряда r(r), d(r) - дельта-функция Дирака. Аналогично для описания магнитостатич. поля стационарной системы электрич. токов с плотностью j(r )вводится симметричный псевдотензор магн. К. м.: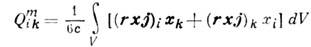

В случае изменяющихся во времени систем электрических зарядов и токов выражения для электрич.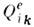 и магн. 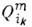К. м. характеризуют полное электромагнитное поле, создаваемое этими системами (см. Квадрупольное излучение). Лит.: Ландау Л. Д., Лифшиц Е. М., Теория поля, 7 изд., М., 1988; Джексон Д ж., Классическая электродинамика, пер. с англ., М., 1965; Баранова Н. Б., Зельдович Б. Я., Два подхода к учету пространственной дисперсии в молекулярном рассеянии света, "УФН ", 1979, т. 127, с. 421; Дубовик В. М., Тосунян Л. А., Тороидные моменты в физике электромагнитных и слабых взаимодействий, "ЭЧАЯ ", 1983, т. 14, с. 1193. В. В. Кочаровский, Вл. В. Кочаровский.