Akademik

- множество, точки к-рого задаются набором чисел (координат), причём при переходе от точки к точке координаты меняются непрерывно. Локально, т. е. в нек-рой окрестности каждой точки, M. устроено так же, как евклидово пространство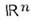. (элементы к-рого представляют собой наборы n вещественных чисел 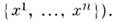M. являются конфигурац. и фазовые пространства динамических систем. Напр., положение твёрдого тела, закреплённого в одной точке, задаётся углами Эйлера 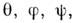так что его конфигурац. пространство является 3-мерным M. [оно совпадает с группой 3-мерных вращений SO(3)]. M. являются также непрерывные группы и однородные пространства (см. Группа). Понятие M. возникло в результате обобщения понятия поверхности; применяется в разл. областях теоретич. физики (аналитич. механика, теория тяготения, квантовая теория поля, теория калибровочных полей и др.). Часто в физике используют M. с дополнительными математическими структурами, например M. со связностью.

Наличие координат позволяет распространить на произвольное дифференцируемое M. мн. методы матем. анализа, развитые первоначально для 3-мерного евклидова пространства 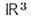(см. Векторный анализ), а затем перенесённые в n-мерное евклидово пространство 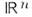Гл. трудностью является то, что в M., как правило, нет выделенной системы координат (подобной декартовой системе координат в . Поэтому приходится рассматривать все возможные системы координат и строить теорию так, чтобы можно было переходить от одной системы координат к другой. Напр., в теории тяготения, где предполагается, что пространство-время является римановым M. (см. Риманово пространство), требование, чтобы ур-ния не зависели от выбора системы координат, является одним из важных принципов (принцип общей ковариантности).

В дифференц. геометрии (т. н. матем. анализ на M.) всё большее распространение получают бескоординатные методы, в к-рых координаты явно не фигурируют (по крайней мере при нек-рых общих доказательствах и рассуждениях). Это удобно и важно с точки зрения физ. приложений, т. к. позволяет отвлечься от несуществ, деталей (связанных с выбором конкретной системы координат) и сделать явным инвариантный характер используемых матем. объектов (отсутствие зависимости от системы координат). В 3-мерном анализе аналогом такого подхода является использование вектора a вместо его компонент a_i, i = 1, 2, 3 (к-рые меняются при изменении системы отсчёта). Разумеется, в бескоординатном подходе неявно всегда присутствуют координаты, т. к. они необходимы для определения всех осн. понятий.

В физ. приложениях M. часто возникают как подмножества в евклидовом пространстве, заданные с помощью ур-ний. Напр., двумерная сфера S² определяется как поверхность в 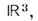выражаемая ур-нием 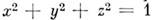; n-мерная сфера Sⁿ определяется как множество точек в 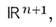выделяемых ур-нием 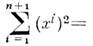1 (здесь х ⁱ- декартовы координаты в 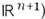; независимые ур-ния 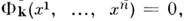k=1, ..., n, выделяют в 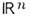M. размерности n- т. Системы координат. Каждая система координат на многообразии M определяется в нек-рой области 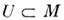и сопоставляет каждой точке этой области, 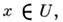набор вещественных чисел (координат этой точки). При этом область U (координатная окрестность) взаимно однозначно отображается на некоторую область евклидова пространства 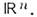Именно возможность такого отображения позволяет перенести в M. аналитич. методы, развитые первоначально на 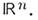Напр., на сфере S ² пара чисел { х, у}может служить координатами точек верх, полусферы (z > 0) или ниж. полусферы (z< 0). Однако её нельзя рассматривать как систему координат на всей сфере, т. к. иначе двум разным точкам сопоставлялся бы один и тот же набор координат. Сферич. координаты 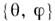определяют ф-лами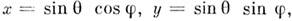

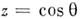
на всей сфере S², за исключением её полюсов (точек 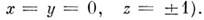Числа 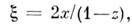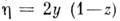(получающиеся при т. н. стереографич. проекции сферы S² на плоскость) могут служить координатами на всей сфере, за исключением её северного полюса (точки х = у = 0, z =1).

Двумерная сфера 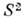- пример M., на к-ром не только не существует выделенной системы координат, но к-рое вообще нельзя покрыть единой системой координат. Причина в том, что сфера радикально отличается от плоскости 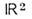своими топологич. свойствами, т. е. не может быть непрерывным образом деформирована в плоскость (см. Топология). Чтобы иметь координаты в окрестности каждой точки сферы, необходимо рассмотреть более одной системы координат. В общем случае в M. вводят целое семейство систем координат так, чтобы области их определения (координатные окрестности) в совокупности покрывали всё M. Каждую систему координат из этого семейства наз. картой, а всё семейство - атласом. Для согласования карт друг с другом используют ф-ции перехода между ними. Если области определения 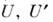двух карт имеют общие точки, то каждой такой точке 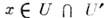сопоставляют два разл. набора координат и 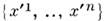. Тем самым определяются ф-ции перехода 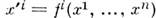, к-рые должны быть непрерывными.

То же самое делают для каждой пары карт из атласа. M. наз. дифференцируемым (класса 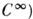, если все возникающие при этом ф-ции перехода бесконечно дифференцируемы. Иногда требуют лишь дифференцируемости до порядка p(M. класса .

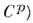Напр., стандартная структура M. на сфере S² (согласованная со структурой объемлющего евклидова пространства 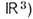задаётся атласом из 3 карт: сферич. координатами 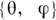вне полюсов, координатами 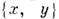в верх, полусфере и координатами 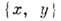в ниж. полусфере. При этом сфера оказывается (бесконечно) дифференцируемым M. Структуру M. на S ² можно определить эквивалентным атласом из 2 карт: 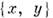в верх, полусфере и стереографич. координаты 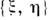на всей сфере, за исключением северного полюса. Эквивалентность 2 атласов означает, что ф-ции перехода между любыми 2 картами обоих атласов дифференцируемы.

Дифференцируемые отображения. Наличие координат позволяет определить понятие дифференцируемой ф-ции на M., опираясь на известное понятие дифференцируемой ф-ции числовых переменных. Если ф-ция 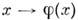задана в каждой точке 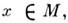то в координатной окрестности её можно записать как ф-цио координат точки 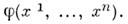Если использование каждой карты, входящей в атлас, приводит при этом к дифференцируемой ф-ции числовых переменных, то исходная ф-ция на M. наз. дифференцируемой.

В приложениях часто рассматривают не только числовые ф-ции на M., но и отображения одного M. на другое, 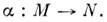При этом многообразия M

и N могут иметь любые размерности. Напр., параметризованную кривую на M. можно считать отображением 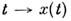вещественной прямой 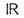(область изменения параметра) в данное M. Др. примером могут служить взаимно однозначные отображения M. на себя,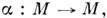к-рые обычно наз. прообразованиями M. Важную роль в физике играют преобразования симметрии.

Выбирая в многообразиях M и N системы координат 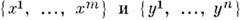, можно по отображению а:

построить набор ф-ций числовых переменных: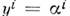

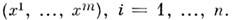Если при любом выборе карт в M и JV эти ф-ции оказываются дифференцируемыми, то отображение a наз. дифференцируемы м. Дифференцируемое отображение наз. диффеоморфизмом, если оно взаимно однозначно и обратное к нему также дифференцируемо. Важную роль играют диффеоморфизмы M. на себя, называемые также дифференцируемыми преобразованиями. В физ. приложениях возникают группы диффеоморфизмов (преобразований), сохраняющих ту или иную дополнит, матем. структуру на M.

Напр., преобразования, сохраняющие метрику риманова пространства, образуют группу его изометрий, или движений. В частности, преобразования, сохраняющие метрику n -мерного евклидова пространства, наз. ортогональными и образуют группу О(п). Дифференцируемое преобразование симплектического многообразия, сохраняющее симплектическую структуру, наз. симп-лектич. диффеоморфизмом. Если симплектич. структуру интерпретировать как гамильтонову структуру на фазовом пространство, то симплектич. диффеоморфизм наз. каноническим преобразованием (см. Гамильтонов формализм).

Дифференцируемое преобразование 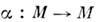порождает некоторое преобразование 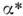пространства всех дифференцируемых ф-ций на M. Ф-ции 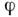сопоставляется при этом новая ф-ция 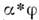, значения к-рой находят по ф-ле 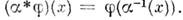В дальнейшем под отображениями всегда будут иметься в виду дифференцируемые отображения.

Векторные поля. Важную роль в матем. анализе играет операция дифференцирования. В евклидовом пространстве из-за существования выделенных декартовых координат достаточно удобным является дифференцирование по координатам. В произвольном M., где все координаты равноправны, вводят понятие инвариантного (не зависящего от выбора координат) дифференцирования. В результате возникают понятия ка-сат. вектора и векторного поля, а также дифференцирования вдоль касат. вектора и вдоль векторного поля.

Если имеется 2-мерная поверхность в 3-мерном евклидовом пространство, то в каждой точке можно провести к этой поверхности касат. вектор, а все векторы, касающиеся поверхности в данной точке, образуют касат. плоскость. В теории M. понятие касат. вектора и касат. пространства необходимо определить внутр. образом, но обращаясь к вложению M. в евклидово пространство. Для этого вектор, касающийся M. в нек-рой точке, интерпретируют как задающий нек-рое направление в этой точке и скорость движения по этому направлению. Направление и скорость движения вдоль него можно охарактеризовать при помощи параметризов. кривой, целиком лежащей в M. и проходящей через данную точку. Это и служит основой для определения касат. вектора в произвольном M.

Пусть на многообразии M задана гладкая кривая 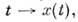проходящая через точку 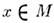,т. е. удовлетворяющая условию 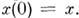Вводя в окрестности точки c систему координат, получим описание кривой при помощи числовых ф-ций 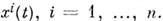Такая кривая определяет в точке x касательный вектор X, а числа 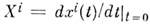являются компонентами этого вектора по отношению к данной системе координат. Разумеется, другая кривая, 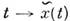, проходящая через точку c и касающаяся первой кривой в этой точке (т. е. такая, что 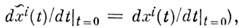определяет тот же самый касат. вектор. Поэтому вектор X соответствует целому пучку касающихся друг друга кривых. Все касат. векторы в данной точке 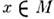образуют векторное пространство размерности га, называемое касательным пространство м и обозначаемое T_x. Касат. вектор является геом. объектом, т. е. он не зависит от системы координат; его компоненты при переходе от одной координатной системы к другой преобразуются по закону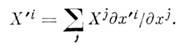

Объединение всех касат. пространств к M. образует новое M., наз. касат. расслоением над первонач. M. Касат. вектор 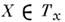позволяет сопоставить каждой (дифференцируемой) ф-ции f на M число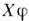 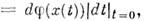называемое производной ф-ции вдоль данного вектора. Через компоненты вектора эта производная выражается в виде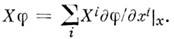

При переходе к др. системе координат это выражение остаётся неизменным, в чём проявляется инвариантный характер понятия касат. вектора и дифференцирования вдоль него. При дифференцировании произведения двух ф-цин выполняется правило Лейбница:

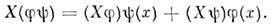
Если в каждой точке 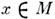задан касат. вектор 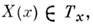то говорят, что на M задано векторное поле X. Если компоненты этого поля 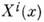являются гладкими ф-циями в любой карте из атласа, то векторное поле наз. дифференцируемым. Векторное поле X сопоставляет каждой ф-ции j на M новую ф-цию 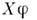со значениями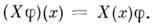

Она наз. результатом дифференцирования ф-ции 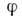вдоль векторного поля X.T. о., чтобы продифференцировать ф-цию вдоль векторного поля, нужно продифференцировать её вдоль каждого вектора 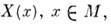и полученные числа считать значениями новой ф-ции. При этом дифференцируемая ф-ция переводится гладким векторным полем в дифференцируемую, причём выполняется правило Лейбница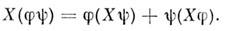

Векторное поле X как инвариантный (не зависящий от выбора координат) объект часто отождествляют с оператором дифференцирования вдоль этого поля. В нек-рой координатной окрестности U этот оператор представляют в виде 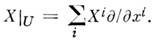При переходе к др. системе координат получается др. выражение 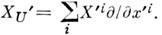Однако на пересечении координатных окрестностей, 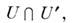эти выражения совпадают благодаря закону преобразования компонент векторного поля 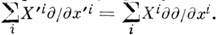Такое совпадение является отражением геом. (инвариантного) характера векторного поля и соответствующего дифференциального оператора.

Дифференциальные операторы, соответствующие двум векторным полям X и Y, можно прокоммутировать, полученный оператор [X, Y]= XY- YХ снова является дифференциальным, т. е. соответствует нек-рому векторному полю. Это векторное поле наз. коммутатором исходных векторных полей, его компоненты в нек-рой системе координат равны

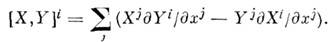
Все (дифференцируемые) векторные поля образуют Ли алгебру относительно операции коммутирования.

Группы преобразований. Векторное поле X задаёт в каждой точке M. направление и скорость движения в этом направлении. Если двигаться в заданных направлениях с заданными скоростями, то все точки M. будут постепенно перемещаться, т. е. определяется семейство преобразований M., зависящее от параметра, 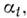причём 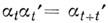, т. е. это семейство представляет собой однопараметрич. группу преобразований. В общем случае векторное поле определяет однопараметрич. группу преобразований лишь локально, т. е. в нек-рой окрестности каждой точки и для нек-рого интервала изменения параметра. Если группа определена глобально (на всём многообразии и для всех значений параметра), векторное поло наз. полным. На компактных M. все гладкие векторные поля являются полными.

Обратно, если задана однопараметрич. группа преобразований 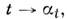то определяется векторное поле 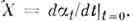Дифференцирование вдоль такого поля описывается ф-лой: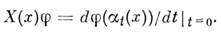

Связь между векторным полем и группой преобразований можно выразить в виде 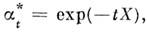где X- дифференц. оператор, а экспонента определена разложением в ряд. В этой ф-ле оператор X выступает как генератор однопараметрич. группы преобразований.

Группа преобразований a_t определяет для каждой точки 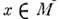кривую к-рая 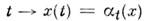проходит через эту точку и имеет в этой точке касат. вектор 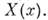T. о., на M. определяется семейство кривых, касательных к векторному полю X. В координатной окрестности U эти кривые являются решениями системы дифференц. ур-ний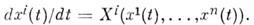

Если 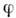- ф-ция на M, то на кривой 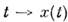она превращается в ф-цию одного параметра, 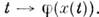Зависимость от этого параметра описывается тогда дифференц. ур-нием 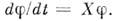T. о., векторные поля позволяют инвариантным образом записывать дифференц. ур-ния на M.

Напр., фазовое пространство гамильтоновой системы с n степенями свободы представляет собой 2n -мерное M., в окрестности каждой точки к-рого можно ввести канонич. координаты 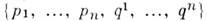(обобщённые импульсы и обобщённые координаты). Разл. канонич. координаты связаны канонич. преобразованиями. Динамика системы задаётся ф-цией Гамильтона H, определённой на фазовом пространстве. Векторное поле в этом пространстве, к-рое в канонич. координатах имеет вид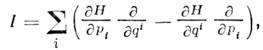

наз. гамильтоновым полем.

В каждой точке это поле касательно к интегральной кривой ур-ний Гамильтона, а соответствующая этому полю однопараметрич. группа преобразований фазового пространства,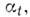описывает эволюцию системы с точением времени. Если 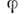- ф-ция на фазовом пространстве, то её изменение с течением времени описывается ур-нием 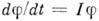. Это ур-ние можно записать при помощи Пуассона скобок: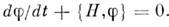

Преобразование M. a естеств. образом определяет не только преобразование 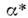ф-ций на этом M., но и преобразование 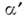векторных полей. Если векторное поле X соответствует однопараметрич. группе преобразований 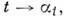то повое поле 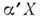определяется группой 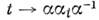. Можно определить это поле и непосредственно, где векторные поля справа и слева следует понимать как диффереиц. операторы в пространстве ф-ций.

Если векторное поле X порождено группой преобразований 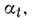то коммутатор двух векторных полей можно выразить через эту группу: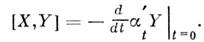

Напр., пусть G - группа Ли (см. Группа )и R_g, L_g - операторы (преобразования) правого и левого сдвигов на ней, 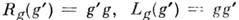. Тогда каждой однопараметрич. подгруппе 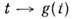в группе G соответствует однопараметрич. группа преобразований группы G, понимаемой как M.,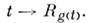Эта группа в свою очередь порождает векторное поле 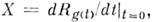инвариантное относительно левого сдвига (левоинвариант-ное), 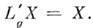Все такие поля образуют алгебру Ли, изоморфную алгебре Ли группы G. Другую реализацию алгебры Ли группы G образуют все правоинвариантные векторные поля, порождаемые группами преобразований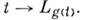

Лит.: Номидзу К., Группы Ли и дифференциальная геометрия, пер. е англ., M., 1960; Бишоп Р., Криттенден Р., Геометрия многообразий, пер. с англ., M., 1967; Арнольд В. И., Математические методы классической механики, 2 изд., M., 1979; Дубровин Б. А., Hовиков С. П., Фоменко А. Т., Современная геометрия, 2 изд., M., 1986; Шутц Б., Геометрические методы математической физики,

пер. с англ., M., 1984; Рихтмайер Р., Принципы современной математической физики, пер. с англ., т. 2, M., 1984.

M. Б. Менский.