Akademik

(измеримая, или физическая, величина) в квантовой механике - физ. величина, удовлетворяющая след. требованиям: 1) для физ. систем существуют состояния, в каждом из к-рых рассматриваемая величина с достоверностью имеет вполне определённое характерное для этого состояния значение (наз. собственным значением данной величины); 2) в результате измерения рассматриваемой величины в любом произвольном состоянии физ. системы получается одно из её собств. значений. Состояние, в к-ром физ. величина принимает то или иное собств. значение, наз. её собственным состоянием, отвечающим (или принадлежащим) данному собств. значению. Одному и тому же собств. значению может принадлежать неск. собств. состояний рассматриваемой физ. величины, отличающихся значениями, к-рые принимают в них к.-л. др. величины. В этом случае собств. значение величины наз. вырожденным. (Так, собств. значению квадрата угл. момента принадлежит неск. собств. состояний, отличающихся значениями проекции момента на произвольную ось в пространстве.) Требование 1 представляет собой условие повторяемости измерения физ. величины по крайней мере для не-

к-рых определ. состояний физ. системы. Действительно, если физ. система находится в состоянии, представляющем к.-л. собств. состояние физ. величины, то любые повторные измерения этой величины будут всегда давать определ. результат - её собств. значение в данном состоянии. Отсутствие же собств. состояний означало бы, что у физ. систем нет состояний в к-рых повторные измерения величины давали бы тот же результат, и поэтому эту величину нельзя рассматривать в качестве измеримой, т. е. наблюдаемой, или физической.

Из принципа суперпозиции состояний (см. Суперпозиции принцип )и требования 2, предъявляемого физ. величине, следует, что любое физ. состояние системы может быть представлено в виде суперпозиции собств. состояний физ. величины, т. е. собств. состояния образуют полную систему векторов состояния. Аналогичными свойствами обладают собств. векторы линейного эрмитового оператора, собств. значения к-рого являются действит. числами. Поэтому в качестве одного из постулатов квантовой механики принимается то, что каждой физ. величине соответствует линейный оператор, собств. значения к-рого равны собств. значениям физ. величины, а собств. векторы являются собств. состояниями физ. величины, принадлежащими данному собств. значению.

Две физ. величины являются одновременно измеримыми, если существуют состояния, в к-рых обе эти величины с достоверностью принимают одновременно свои собств. значения (т. е. собств. состояния одной из них являются одновременно собств. состояниями другой). Необходимым и достаточным условием этого является условие коммутативности операторов, отвечающих этим величинам. Если две величины А и В не измеримы одновременно, то теряет прямой смысл понятие произведения этих величин, т. к. оператор произведения двух некоммутирующих эрмитовых операторов А ^{^} и В ^{^} физ. величин не будет эрмитовым (т. е. не может

отвечать к.-л. физ. величине) (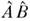)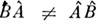⁺ =. Однако в этом случае можно определить т. н. симмет-ризов. произведение двух величин как величину, к-рой соответствует эрмитов оператор ¹/₂(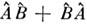). Состояние физ. системы может быть определено путём задания нек-рой совокупности физ. величин, характеризующих систему (т. н. полного набора измеряемых величин). Очевидно, что физ. величины, входящие в полный набор, должны быть измеримы одновременно, т. е. их операторы должны коммутировать.

Лит. см. при ст. Квантовая механика. С. С. Герштейн.