- ОСЦИЛЛЯЦИИ
-
элементарных частиц -периодический во времени и пространстве процесс превращения частиц определ. совокупности друг в друга. В простейшем случае О. двух частиц А и В (или, что то же самое, О. в системе частиц А и В)- периодич. процесс полного или частичного перехода А в . и обратно: А
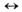 В.
В.
Первый и наиб. хорошо изученный пример- О. в системе нейтральных К-мезонов: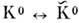 . Теоретич. предсказание и обсуждение эксперим. следствий О.
. Теоретич. предсказание и обсуждение эксперим. следствий О.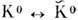 были даны А. Пайсом (A. Pais) и О. Пиччони (О. Piccioni) в 1955 (эффектПайса - Пиччони, обнаруженный и исследованный в 1957 - 61). В 1957 Б. М. Понтекорво высказал предположение о существовании др. пар нейтральных частиц, у к-рых не запрещены переходы частица - античастица и к-рые, следовательно, должны осциллировать. В этой связи предложены пока гипотетические О. мюоний- антимюоний (связанные системы
были даны А. Пайсом (A. Pais) и О. Пиччони (О. Piccioni) в 1955 (эффектПайса - Пиччони, обнаруженный и исследованный в 1957 - 61). В 1957 Б. М. Понтекорво высказал предположение о существовании др. пар нейтральных частиц, у к-рых не запрещены переходы частица - античастица и к-рые, следовательно, должны осциллировать. В этой связи предложены пока гипотетические О. мюоний- антимюоний (связанные системы 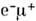 и
и 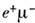 ) и нейтрино -антинейтрино. В обоих случаях необходимым является взаимодействие, нарушающеесохранение ленточного числа. В 1962 З. Маки (Z. Maki), М. Накагава(М. Nakagawa) и С. Саката (Sh. Sakata) теоретически, рассмотрели случайО. нейтрино разных типов:
) и нейтрино -антинейтрино. В обоих случаях необходимым является взаимодействие, нарушающеесохранение ленточного числа. В 1962 З. Маки (Z. Maki), М. Накагава(М. Nakagawa) и С. Саката (Sh. Sakata) теоретически, рассмотрели случайО. нейтрино разных типов: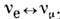 В 1985 в протон-антипротонных соударениях коллаборацией UA1 в ЦЕРНе былиобнаружены события, свидетельствующие об О. нейтральных В s -мезонов:
В 1985 в протон-антипротонных соударениях коллаборацией UA1 в ЦЕРНе былиобнаружены события, свидетельствующие об О. нейтральных В s -мезонов: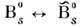 (аналогах
(аналогах  для мезонов с
для мезонов с 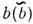 -и
-и 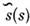 -кварками).В 1987 в экспериментах на накопительном кольце е + е - вДЕЗИ (детектор АРГУС) наблюдались эффекты О. мезонов, состоящих из b- и d -кварков,
-кварками).В 1987 в экспериментах на накопительном кольце е + е - вДЕЗИ (детектор АРГУС) наблюдались эффекты О. мезонов, состоящих из b- и d -кварков,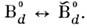 Должны существовать также О.
Должны существовать также О.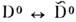 , но ожидаемые эффекты очень малы (далеко за пределами чувствительностисуществующих экспериментов). Ведутся поиски О. нейтрон - антинейтрон, предсказываемыхв теориях с нарушением сохранения барионного числа. Обсуждаютсяэкзотич. каналы, такие, как фотон - аксион и др.
, но ожидаемые эффекты очень малы (далеко за пределами чувствительностисуществующих экспериментов). Ведутся поиски О. нейтрон - антинейтрон, предсказываемыхв теориях с нарушением сохранения барионного числа. Обсуждаютсяэкзотич. каналы, такие, как фотон - аксион и др.Осцилляции и смешивание частиц. О. А
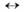 В естьследствие смешивания частиц А и В. В вакууме это смешиваниевыражается в том, что состояния
В естьследствие смешивания частиц А и В. В вакууме это смешиваниевыражается в том, что состояния 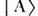 и
и 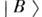 являютсякогерентными комбинациями двух состояний
являютсякогерентными комбинациями двух состояний 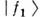 и
и 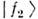 с определёнными, но различающимися массами m1 и m2 (сами . и . определённых масс не имеют):
с определёнными, но различающимися массами m1 и m2 (сами . и . определённых масс не имеют):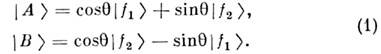
Коэф. (1) выбраны из условия ортонормированности, угол
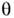 наз. углом смешивания в вакууме (рис. 1). Согласно (1), смешивающиеся . и . состоятиз одних и тех же компонент f1 и f2,но различаются величинами их примесей, а также разностью фаз
наз. углом смешивания в вакууме (рис. 1). Согласно (1), смешивающиеся . и . состоятиз одних и тех же компонент f1 и f2,но различаются величинами их примесей, а также разностью фаз 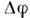 между их состояниями. В
между их состояниями. В 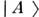 составляющие
составляющие 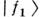 и
и 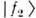 находятсяв фазе
находятсяв фазе 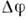 = 0, в
= 0, в 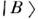 - в противофазе
- в противофазе 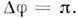 Максимальным смешиванием наз. случай, когда
Максимальным смешиванием наз. случай, когда 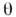 = 45°; при этом
= 45°; при этом 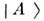 и
и 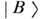 различаютсятолько разностью фаз, примеси состояний
различаютсятолько разностью фаз, примеси состояний 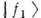 и
и 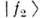 вних равны.
вних равны.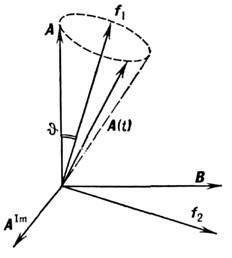
Рис. 1. Графическое представление смешиванияи осцилляции. Состояниям с определёнными массами и взаимодействиями сопоставляютсядва ортонормированных базиса в действительных плоскостях {fi,f2} и {А, В}. Смешивание выражается в повороте базисов друг относительно друга наугол
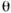 .Эволюция состояния |A(t)> описываетсявращением единичного вектора A(t )по поверхности конуса с угломраствора
.Эволюция состояния |A(t)> описываетсявращением единичного вектора A(t )по поверхности конуса с угломраствора 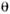 .Период вращения Т = T осц. Проекция A(t )на плоскость{А, А Im} равна амплитуде вероятности обнаружить частицу . вмомент t[AIm соответствует мнимой части состояния |A(t)>].
.Период вращения Т = T осц. Проекция A(t )на плоскость{А, А Im} равна амплитуде вероятности обнаружить частицу . вмомент t[AIm соответствует мнимой части состояния |A(t)>].О. возникают в процессе эволюции сложногосостояния, рождённого как состояние
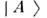 или
или 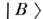 ,т. е. необходимым условием возникновения О. является рождение частиц . илиВ - "приготовление" одной из когерентных комбинаций (1). Частицы А и . рождаютсяи поглощаются в определ. взаимодействиях. Они характеризуются определ. различающимися квантовыми числами ( ароматами F А, FB), к-рые в этих взаимодействиях сохраняются. Поэтому в данной конкретнойреакции рождается либо частица А, либо частица В. В этойсвязи состояния
,т. е. необходимым условием возникновения О. является рождение частиц . илиВ - "приготовление" одной из когерентных комбинаций (1). Частицы А и . рождаютсяи поглощаются в определ. взаимодействиях. Они характеризуются определ. различающимися квантовыми числами ( ароматами F А, FB), к-рые в этих взаимодействиях сохраняются. Поэтому в данной конкретнойреакции рождается либо частица А, либо частица В. В этойсвязи состояния 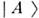 и
и 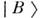 наз. собственными состояниями взаимодействий или состояниями с определ. ароматами. Напр., в случае
наз. собственными состояниями взаимодействий или состояниями с определ. ароматами. Напр., в случае 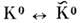 - это сильное взаимодействие, сохраняющее странность: F = S, причём S (К°)- = + l,
- это сильное взаимодействие, сохраняющее странность: F = S, причём S (К°)- = + l,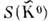 = - 1. В случае О.
= - 1. В случае О.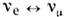 нейтрино v е или
нейтрино v е или 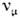 рождаются в слабом взаимодействии, обусловленном заряженнымитоками, а ароматами являются электронное (L е) илимюонное
рождаются в слабом взаимодействии, обусловленном заряженнымитоками, а ароматами являются электронное (L е) илимюонное 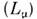 лептонные числа: Le(ve) = 1, Le(
лептонные числа: Le(ve) = 1, Le(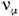 )= 0,
)= 0,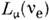 =0,
=0,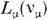 = 1.
= 1.
Смешивание А и .(1) обусловленодополнит. взаимодействием типа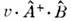 + э. с., переводящим А в В и наоборот (здесь v - параметрразмерности массы в случае фермионов и квадрата массы в случае бозонов;
+ э. с., переводящим А в В и наоборот (здесь v - параметрразмерности массы в случае фермионов и квадрата массы в случае бозонов;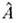 ,
,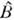 - операторы полей соответствующих частиц; э. с. - эрмитово-сопряжённыйчлен). Это взаимодействие имеет вид недиагонального массового члена в гамильтониане, и массовая матрица частиц А и В оказывается недиагональной. Следовательно, А и В действительно не имеют определ. масс;таковыми обладают новые состояния
- операторы полей соответствующих частиц; э. с. - эрмитово-сопряжённыйчлен). Это взаимодействие имеет вид недиагонального массового члена в гамильтониане, и массовая матрица частиц А и В оказывается недиагональной. Следовательно, А и В действительно не имеют определ. масс;таковыми обладают новые состояния 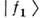 и
и 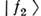 -комбинации
-комбинации 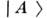 и
и 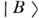 ,к-рые диагонализуют массовую матрицу [эти комбинации можно получить, разрешаясистему (1) относительно
,к-рые диагонализуют массовую матрицу [эти комбинации можно получить, разрешаясистему (1) относительно 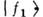 и
и 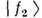 ].В результате диагонализации фиксируются массы частиц f1 и f2,а также угол смешивания: tg(2
].В результате диагонализации фиксируются массы частиц f1 и f2,а также угол смешивания: tg(2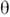 )~ v. Состояния
)~ v. Состояния 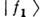 и
и 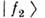 частоназ. собственными состояниями массовой матрицы. Вакуумное смешивание означает, т. о., несовпадение собств. состояний взаимодействий и собств. состояниймассовой матрицы.
частоназ. собственными состояниями массовой матрицы. Вакуумное смешивание означает, т. о., несовпадение собств. состояний взаимодействий и собств. состояниймассовой матрицы.
Дополнит. взаимодействие, приводящее ксмешиванию, явно нарушает аромат (квантовые числа) частиц А, В, и, как следствие этого, в процессе О. аромат не сохраняется. Для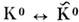 |
| S|=2, для
S|=2, для 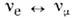 |
|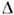 Le| = 1, |
Le| = 1, |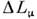 |= 1 и т. д.
|= 1 и т. д.Основные параметры осцилляции. О. возникают в процессе эволюции в пространстве-времени смешивающихся состояний(1). Говорят об О. аромата (странности, красоты, чисел Le,
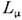 и др.) в данном смешанном состоянии.
и др.) в данном смешанном состоянии.
Распространение частицы, рождённой, напр.,как А, описывается суперпозицией двух волновых пакетов, соответствующихсостояниям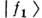 и
и 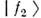 .Именно
.Именно 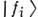 , являясь собств. состояниями гамильтониана в вакууме, обладают определённымиэнергиями и фазовыми скоростями, они эволюционируют независимо, и долиих примесей сохраняются. Из-за различия в массах пакеты
, являясь собств. состояниями гамильтониана в вакууме, обладают определённымиэнергиями и фазовыми скоростями, они эволюционируют независимо, и долиих примесей сохраняются. Из-за различия в массах пакеты 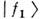 и
и 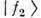 имеютразные фазовые
имеютразные фазовые скорости:
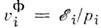 , где
, где 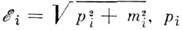 и mi- соответственно полная энергия, импульс и масса частицы fj (принята система единиц, в к-рой с =1). Поэтому в процессе распространенияразность фаз между
и mi- соответственно полная энергия, импульс и масса частицы fj (принята система единиц, в к-рой с =1). Поэтому в процессе распространенияразность фаз между 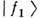 и
и 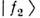 будетизменяться. Если пакеты достаточно короткие, то разность фаз в любой точкепакетов примерно одинакова и равна разности фаз соответствующих плоскихволн:
будетизменяться. Если пакеты достаточно короткие, то разность фаз в любой точкепакетов примерно одинакова и равна разности фаз соответствующих плоскихволн: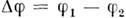 ,где
,где 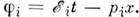 Состояние, рождённое как
Состояние, рождённое как 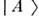 ,в произвольный момент времени t имеет вид
,в произвольный момент времени t имеет вид 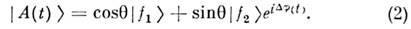
Разности фазовых скоростей и фаз можнооценить, полагая, напр., что импульсы частиц f1 и f2 одинаковы:
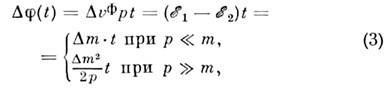
где
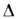 .= т 1-m2,
.= т 1-m2,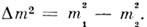 Монотонный рост со временем разности фаз
Монотонный рост со временем разности фаз 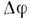 и приводит к О. Действительно, в нач. момент
и приводит к О. Действительно, в нач. момент 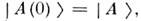 но при t
но при t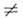 0
0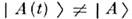 и
и 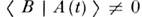 , т. е. в
, т. е. в 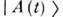 появляетсяпримесь
появляетсяпримесь 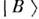 .Этот процесс периодический: к моменту t= Т осц, определяемомуусловием
.Этот процесс периодический: к моменту t= Т осц, определяемомуусловием 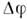 (T осц)=
(T осц)=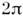 ,система (осциллирующие частицы) окажется в исходном состоянии
,система (осциллирующие частицы) окажется в исходном состоянии 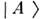 .Согласно (3), период О. равен
.Согласно (3), период О. равен 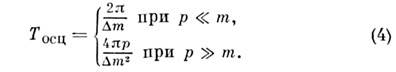
Расстояние, на к-ром система возвращаетсяк исходному состоянию, наз. длиной осцилляции l осц. Вобоих случаях (нерелятивистском и релятивистском)
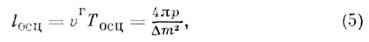
где
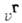 - групповая скорость пакетов. Макс. отличие состояния
- групповая скорость пакетов. Макс. отличие состояния 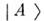 от исходного наблюдается в моменты времени tp, когда
от исходного наблюдается в моменты времени tp, когда 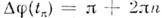 ( п=0, 1, 2...), при этом вероятность обнаружить частицу В определяетглубину осцилляции:
( п=0, 1, 2...), при этом вероятность обнаружить частицу В определяетглубину осцилляции: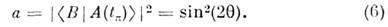
Вероятность обнаружить частицу А в произвольныймомент t равна:
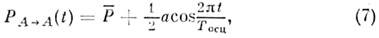 где
где 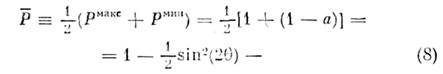
ср. значение, или вероятность, усреднённаяпо периоду (рис. 2). Выражение (7) может быть переписано в наиб. частоиспользуемом виде
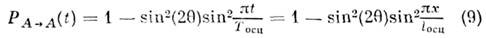
( х - расстояние от точки рождениячастицы А до точки наблюдения). Вероятность перехода А
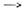 В равна
В равна 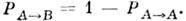
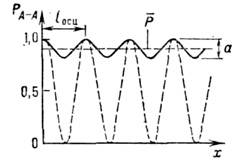
Рис. 2. Пространственная картина осцилляции. Зависимость от расстояния х вероятности обнаружить частицу исходноготипа: сплошная линия - малое смешивание; пунктир - максимальное смешивание.
Глубина О. a и ср. вероятность
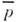 определяютсятолько углом
определяютсятолько углом 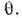 причёмв случае макс. смешивания глубина наибольшая: a =1,
причёмв случае макс. смешивания глубина наибольшая: a =1,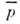 =1/2.
=1/2.
О. являются по существу интерференц. эффектом. Компоненты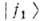 и
и 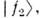 составляющие
составляющие 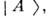 могут быть разложены в соответствии с (1) по состояниям
могут быть разложены в соответствии с (1) по состояниям 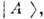
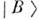 сопредел. ароматами. Т. о. возникают две волны
сопредел. ароматами. Т. о. возникают две волны 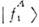 и
и 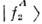 от
от 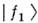 и
и 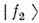 имеющиеодинаковый аромат, но разные фазовые скорости. Эти волны интерферируют, и результат интерференции определяет амплитуду вероятности обнаружить частицу . всостоянии
имеющиеодинаковый аромат, но разные фазовые скорости. Эти волны интерферируют, и результат интерференции определяет амплитуду вероятности обнаружить частицу . всостоянии 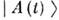 .Из-за различия в фазовых скоростях волн характер интерференции изменяетсяот максимально конструктивной в моменты t=nT ОСц до максимальнодеструктивной при t =(1/2 + n) n = 0, 1, 2... Аналогичноописывается О. FB -аромата.
.Из-за различия в фазовых скоростях волн характер интерференции изменяетсяот максимально конструктивной в моменты t=nT ОСц до максимальнодеструктивной при t =(1/2 + n) n = 0, 1, 2... Аналогичноописывается О. FB -аромата.
Если область генерации частиц или размерыдетектора превышают l осц или если энергетич. разрешениеустановки невелико: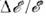 l осц/r, где r - расстояние от источника до детектора, то происходит усреднениеО. и измерения дадут Р = Р. Это усреднение имеет квантовомеханич. природу и соответствует потере когерентности между
l осц/r, где r - расстояние от источника до детектора, то происходит усреднениеО. и измерения дадут Р = Р. Это усреднение имеет квантовомеханич. природу и соответствует потере когерентности между 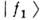 и
и  ,к-рая может быть связана либо с большими размерами волновых пакетов, либос тем, что разность фаз
,к-рая может быть связана либо с большими размерами волновых пакетов, либос тем, что разность фаз 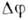 оказывается случайной величиной. (В первом случае в разных точках пакетов
оказывается случайной величиной. (В первом случае в разных точках пакетов 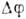 принимает значения от 0 до
принимает значения от 0 до 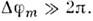 )Интерференция волн
)Интерференция волн 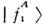 и
и 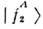 приэтом исчезает.
приэтом исчезает.Обобщения. Аналоги осцилляции. Выделяютдва типа осцилляции: О. частица - античастица
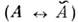 с изменением аромата на двойку, т. е. |
с изменением аромата на двойку, т. е. | F|= 2; О. частиц с разными ароматами, когда |
F|= 2; О. частиц с разными ароматами, когда |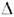 FA|= |
FA|= |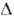 FB| =1.
FB| =1.
Для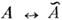 реализуется случай макс. смешивания. Это связано с тем, что в силу теоремыСРТ диагональные элементы массовой матрицы, т. е. амплитуды переходов А
реализуется случай макс. смешивания. Это связано с тем, что в силу теоремыСРТ диагональные элементы массовой матрицы, т. е. амплитуды переходов А 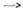 А и
А и 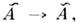 одинаковы. К указанному типу относят О.
одинаковы. К указанному типу относят О.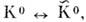
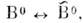
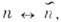 мюоний- антимюоний и др. Взаимодействие осциллирующей системы с веществом и внеш. полями устраняет равенство диагональных элементов, и смешивание становитсяне максимальным.
мюоний- антимюоний и др. Взаимодействие осциллирующей системы с веществом и внеш. полями устраняет равенство диагональных элементов, и смешивание становитсяне максимальным.
Для О. второго типа, по-видимому, типичномалое смешивание, как это имеет место для кварков, а следовательно, и малаяглубина О. Такая ситуация может реализоваться для нейтрино: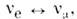
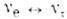
О. имеют ряд аналогов в др. областях физики, прежде всего в механике. По существу это биения в системе слабосвязапныхосцилляторов, напр. маятников. Колебания одного маятника соответствуютраспространению частицы А, колебания другого - распространению частицы В. Связьмежду осцилляторами эквивалентна взаимодействию, переводящему . в В. Периодич. передача колебаний от одного маятника другому и естьаналог О. Осцилляции аналогичны таким явлениям, как вращение плоскостиполяризации света в оптически активных средах, прецессия спина частиц вмагн. поле и др.
В случае смешивания трёх и более частиц(напр., трёх нейтрино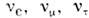 ) осцилляц. вероятности оказываются суперпозициями трёх и более периодич. ф-ций (9). С практич. точки зрения важной характеристикой является наиб, возможное подавление потока исходных частиц в результате усреднения О. Минимизация вероятности
) осцилляц. вероятности оказываются суперпозициями трёх и более периодич. ф-ций (9). С практич. точки зрения важной характеристикой является наиб, возможное подавление потока исходных частиц в результате усреднения О. Минимизация вероятности 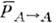 поуглам смешивания даёт для системы N частиц:
поуглам смешивания даёт для системы N частиц: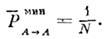
Если при смешивании СР-чётностпъ сохраняется, то вероятности осцилляц. переходов для частиц и античастиц совпадают:
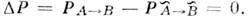 Нарушение СР -инвариантности связано с появлением комплексной фазы
Нарушение СР -инвариантности связано с появлением комплексной фазы 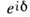 в матрице смешивания. При этом разность вероятностей
в матрице смешивания. При этом разность вероятностей 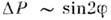 отлична от нуля.
отлична от нуля.
Осцилляциомныс эксперименты. О. непосредственнопроявляются в том, что в пучке частиц, состоящем первоначально из частиц А,в процессе его распространения периодически появляется и исчезает примесьчастиц В. Детекторы, расположенные на разных расстояниях от источника ., будут регистрировать разные примеси В и соответственно разноеподавление исходного А- потока (рис. 2). При фиксиров. расстоянииисточник - детектор и непрерывном энергетич. спектре частиц О. приводятк появлению квазипериодич. структуры на спектре частиц А вследствиезависимости длины О. от энергии [см. (5)].
Картина О. искажается, если одна или обечастицы f1 и f2 распадаются, как этоимеет место, напр., для К 0-, В 0 -мезонов. Распад восциллирующем состоянии (2) описывается дополнит, факторами ехр ( - Г it/2)перед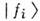 , где Г i - ширина распада частицы fi. Этоприводит к экспоненц. затуханию О.:
, где Г i - ширина распада частицы fi. Этоприводит к экспоненц. затуханию О.: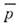 иа уменьшаются.
иа уменьшаются.
Др. фактор, влияющий на О., - расхождениеволновых пакетов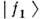 и
и 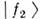 из-заразличия их групповых скоростей. В процессе движения пакеты смещаются друготносительно друга и, т. к. они имеют конечные размеры, их перекрытие уменьшается, соответственно уменьшается глубина О. При полном расхождении пакетов О. исчезают.
из-заразличия их групповых скоростей. В процессе движения пакеты смещаются друготносительно друга и, т. к. они имеют конечные размеры, их перекрытие уменьшается, соответственно уменьшается глубина О. При полном расхождении пакетов О. исчезают.
Параметры О. - глубина, ср. вероятностьи длина - зависят от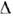 т(
т(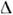 т2 )и
т2 )и 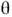 [см.(3), (4), (6)]. Поэтому исследование осцилляц. эффектов является методомизмерения разностей масс (квадратов масс) и углов смешивания. Отрицат. результат поиска О. в предельных случаях может означать, что либо малосмешивание и глубина О. меньше чувствительности эксперим. установки, либомала разность масс (квадратов масс), так что длина О. много больше расстоянияисточник - детектор и О. не успели развиться. Эксперимент при этом даётограничения сверху на
[см.(3), (4), (6)]. Поэтому исследование осцилляц. эффектов является методомизмерения разностей масс (квадратов масс) и углов смешивания. Отрицат. результат поиска О. в предельных случаях может означать, что либо малосмешивание и глубина О. меньше чувствительности эксперим. установки, либомала разность масс (квадратов масс), так что длина О. много больше расстоянияисточник - детектор и О. не успели развиться. Эксперимент при этом даётограничения сверху на 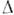 т(
т( т 2 )иsin22
т 2 )иsin22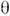 .Поскольку О. являются эффектом нарушения определённых квантовых чисел, их поиск есть метод исследования взаимодействий, нарушающих эти числа.
.Поскольку О. являются эффектом нарушения определённых квантовых чисел, их поиск есть метод исследования взаимодействий, нарушающих эти числа.Осцилляции в веществе. Среда изменяетэволюцию системы смешанных частиц. В случае
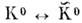 это эффект когерентной регенерации
это эффект когерентной регенерации 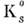 -мезонов, описанный Пайсом и Пиччони (в той же работе, в к-рой были предсказаны О. К°-мезонов) и затем детально исследованный в эксперименте. В 1977 Л. Вольфенштейн(L. Wolfenstein) рассмотрел аналогичный эффект для нейтрино.
-мезонов, описанный Пайсом и Пиччони (в той же работе, в к-рой были предсказаны О. К°-мезонов) и затем детально исследованный в эксперименте. В 1977 Л. Вольфенштейн(L. Wolfenstein) рассмотрел аналогичный эффект для нейтрино.
Влияние среды связано с упругим рассеяниемна нулевой угол осциллирующих частиц А и В на компонентахсреды. Такое рассеяние сводится к появлению у волн, описывающих движение . и В, показателей преломления, а следовательно, к изменению их фазовыхскоростей. Среда модифицирует О., если рассеяние частиц . и . различно. В этом случае между волнами А и В появитсядополнит. разность фаз, а также будут осуществляться переходы между состояниямис определ. массами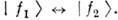 Амплитуды этих переходов пропорц. разности амплитуд рассеяния частиц . и В. Этоозначает, что
Амплитуды этих переходов пропорц. разности амплитуд рассеяния частиц . и В. Этоозначает, что 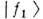 и
и 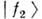 всреде уже не являются собств. состояниями гамильтониана и сами осциллируют. Смешивание
всреде уже не являются собств. состояниями гамильтониана и сами осциллируют. Смешивание 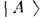 и
и 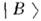 всреде следует определять по отношению к собств. состояниям
всреде следует определять по отношению к собств. состояниям 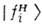 [аналогично тому, как это было сделано в (1)] гамильтониана для даннойсреды с учётом взаимодействий, поскольку именно
[аналогично тому, как это было сделано в (1)] гамильтониана для даннойсреды с учётом взаимодействий, поскольку именно 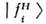 обладают определёнными фазовыми и групповыми скоростями. Т. к. в среде
обладают определёнными фазовыми и групповыми скоростями. Т. к. в среде 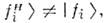 то угол смешивания в веществе
то угол смешивания в веществе 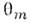 будет отличен от
будет отличен от 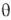 .В однородной среде
.В однородной среде 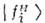 эволюционируютнезависимо, переходов
эволюционируютнезависимо, переходов 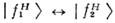 нет (т. е. доли их примесей не меняются). Поэтому качественная карти-шО. оказывается такой же, как в вакууме, но с изменёнными параметрами: ввыражениях для а и
нет (т. е. доли их примесей не меняются). Поэтому качественная карти-шО. оказывается такой же, как в вакууме, но с изменёнными параметрами: ввыражениях для а и 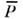 вакуумный угол
вакуумный угол 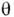 следует заменить на
следует заменить на 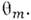 В зависимости от знаков разности амплитуд и
В зависимости от знаков разности амплитуд и 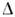 т, величинплотности вещества и энергии среда может как усиливать, так и ослаблятьО.
т, величинплотности вещества и энергии среда может как усиливать, так и ослаблятьО.
Т. о., общим условием возникновения О. является рождение состояний, представляющих собой суперпозицию (когерентнуюсмесь) двух или неск. невырожденных собств. состояний гамильтониана дляданной среды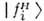 (при этом наличие частиц с ненулевыми массами не обязательно). О. в данномсостоянии
(при этом наличие частиц с ненулевыми массами не обязательно). О. в данномсостоянии 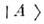 происходят относительно
происходят относительно 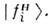 (В вакууме состояния
(В вакууме состояния 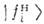 совпадают с состояниями, имеющими определ. массы:
совпадают с состояниями, имеющими определ. массы: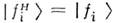 .)Глубина О. есть мера несовпадения
.)Глубина О. есть мера несовпадения 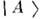 с одним из собств. состояний гамильтониана; длина О. обратно пропорц. разностисобственных значений
с одним из собств. состояний гамильтониана; длина О. обратно пропорц. разностисобственных значений 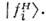
В среде с изменяющейся на пути частицплотностью возникают качественно новые эффекты: в процессе распространениячастиц изменяются и глубина О. и их ср. значение (см. Резонансная конверсиянейтрино).Лит.: Рais A., Piссiоni О., Noteon the decay and absorption of the q°,"Phys. Rev.", 1955, v. 100, p. 1487; Марков M. А., Гипероны и К-мезоны, М., 1958; Биленький С. М., Понтекорво Б. М., Смешивание лептонов и осцилляциинейтрино, "УФН", 1977, т. 123, с. 181; Окунь Л. В., Лептоны и кварки, 2изд., М., 1990; Уральцев Н. Г., Xозе В. А., Смешивание кварков в слабыхвзаимодействиях, "УФН", 1985, т. 146, с. 507.
А. Ю. Смирнов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.