Akademik

ПРОЦЕССЫ в плазме- неравновесные процессы, приводящие к выравниванию пространственных распределенийпараметров плазмы - концентраций, среднемассовой скорости и парциальныхтемп-р электронов и тяжёлых частиц. В отличие от П. п. нейтральных частиц, П. п. в плазме зависят от напряжённостей собственных самосогласованныхэлектрич. Е и магн. В полей, к-рые определяютсятоками и объёмными зарядами частиц плазмы. Поэтому П. п. в плазме в общемслучае описываются системой ур-нии переноса частиц, импульса и энергиии ур-ний Максвелла.
В гидродинамич. приближении, когда смещениячастиц между столкновениями (в отсутствие магп. поля - длина свободногопробега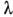 )меньше характерных масштабов неоднородности плазмы L, а характерныечастоты не превосходят частот столкновений v, классические (столкновительные)П. п. описываются матрицей коэф. переноса. Она линейно связывает потокичастиц, импульса и энергии с факторами, нарушающими термодипамич. равновесие,- градиентами парциальных концентраций и темп-р, неоднородностью скорости, электрич. полем (см. Переноса явления). Вследствие большого различиямежду массами электронов и тяжёлых частиц (ионов и нейтральных молекул)темп-ры их, вообще говоря, различны, поэтому перенос энергии лёгкой и тяжёлойкомпонентой рассматривают отдельно. Напр., в отсутствие магн. поля . потоктепла 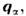обусловленный температурным градиентом 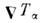к.-л. 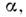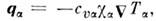компоненты есть где 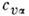-уд. теплоёмкость при пост. ооъёме,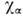- коэф. температуропроводности. Парциальный тензор плотности потока импульса 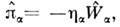где тензор скорости сдвигов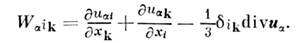

При В = 0 оценки для коэф. температуропроводности 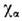и кинематич. вязкости 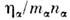в плазме такие же, как и в нейтральных газах: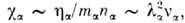где 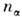-концентрация,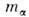- масса частиц компоненты 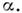Перенос частиц в плазме обусловлен градиентами концентрации (диффузия),темп-ры (термодиффузия) и электрич. полем.
П. п. в слабоионизованной плазме без магнитногоноля. В слабоионизов. плазме, а также в полупроводниках и слабых электролитахимеется выделенная система отсчёта, связанная с нейтральной компонентой(в полупроводниках - с решёткой). Если столкновения заряж. частиц междусобой несущественны, то потоки частиц определяются трением их о нейтральныйгаз и равны в этой системе: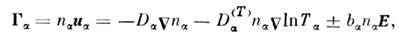

где 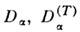- коэф. диффузии, термодиффузии,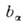- подвижность; при этом 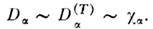Эти коэф. связаны с темп-рой и зарядом частицы 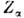соотношением Эйнштейна: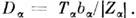Суммарная проводимость плазмы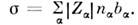
Неоднородность плазмы создаёт самосогласованноенеоднородное электрич. поле, к-рое при медленных процессах определяетсяусловием квазинейтралъности плазмы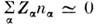 иявляется потенциальным. Простейшим примером влияния самосогласованногоэлектрич. поля на П. п. является амбиполярная диффузия а простой( п _е= n_i = п )слабоионизов. плазме при Т _е = Т =const, к-рая описывается ур-нием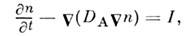

где I соответствует рождению и рекомбинациичастиц, а коэф. амбиполярной диффузии

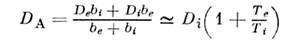
определяется наим. подвижными частицами(ионами). Электрич. поле тормозит электроны и приводит к совместной диффузииэлектронов и ионов, потоки к-рых Г _е, Г _i водномерном случае отличаются на пост. вектор, т. е. плотность тока j= const. При I =0характерное диффузионное время жизни неоднородности 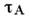=L²/ D_A, где L - характерный размернеоднородности. Эта ситуация является вырожденной: ур-ние не содержит явноэлектрич. поля и не зависит от тока, протекающего через неоднородную плазму.
Диффузия в плазме с ионами разных сортовдаже при j= 0 не сводится к амбиполярной, т. к. электрич. полеоказывается пропорциональным градиентам всех парциальных концентраций. При этом нек-рые потоки частиц могут быть направлены в сторону возрастанияих концентрации. В многокомпонентной плазме или в случае, когда подвижностизависят от электрич. поля, протекание пост. тока приводит к движению неоднородностейсо скоростью амбиполярного дрейфа. В плазме, содержащей k сортовзаряж. частиц с пост. подвижностями, имеется (k -2) разл. значенийскорости амбиполярного дрейфа, соответствующих разным типам сигналов. Напр.,если имеются ионы двух сортов (i₁, i₂ )с подвижностями b_i1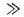b_i2,то при n_i2 = const скорость амбиполярного дрейфа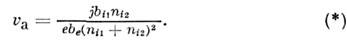

В простой газоразрядной плазме обычно существенназависимость подвижности электронов от электрич. поля b _е (Е). При этом 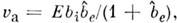где 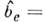= д(lnb _е)/д(ln Е). Скоростьамбиполярного дрейфа v_a характеризует распространениеквазинейтральных возмущений концентрации (волн плотности) плазмы. Большиевозмущения (как волны большой амплитуды) из-за нелинейной связи между концентрациямии скоростями потоков (*) деформируются и опрокидываются. Возникают областис резкими градиентами концентрации - скачки, аналогичные ударным волнам,- где существенна диффузия или нарушается квазинейтральность. Если же масштабнеоднородностей L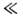Т/(еЕ), тоэволюция их и при наличии тока определяется лишь диффузией.

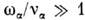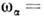
П. п. в слабоионизованной плазме в магнитномполе. Т. к. смещение заряж. частиц поперёк магн. поля В уменьшаетсяс ростом В, то коэф. переноса являются тензорами: вдоль В их компоненты такие же, как и при В = 0, а поперёк -малы. При (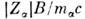- циклотронная частота) в слабоионизов. плазме поперечные диагональныеэлементы тензоров диффузии имеют вид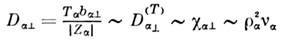

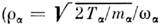- ларморовский радиус). В сильном магн. поле 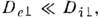тогда как 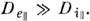Недиагональные (холловские) компоненты тензоров подвижности в этих же условиях 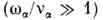соответствуют дрейфу в скрещенных полях: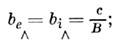

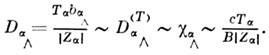
Даже в простой слабоионизов. плазме в магн. поле перенос частиц не сводится к амбиполярной диффузии. Для её реализациибыл бы необходим электрич. потенциал, тормозящий во всех направлениях наиб. подвижные частицы (электроны - вдоль В; ионы - поперёк В). Такой потенциал, как правило, не удовлетворяет граничным условиям иможет реализоваться лишь в исключит. случаях. Поэтому и ур-ние амбиполярнойдиффузии описывает лишь одномерную эволюцию поперёк В, атакже эволюцию профилей вида n(r,z) =n₁(r)n₂(z)(z - координата вдоль В, r - поперёк В) в диэлектрич. баллоне или в неограниченной плазме (в последнем случаетакой профиль реализуется лишь при очень сильном превышении возмущённойконцентрации над фоновой). Характерное диффузионное время жизни при этом

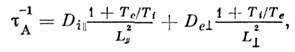
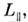
где 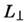- размеры неоднородности вдоль и поперёк В. В общем случае условие квазинейтральноститребует равенства divГ _e = divF_i и по плазмепротекает вихревой ток. Тогда эволюция может определяться не наименьшими, а наибольшими коэф. диффузии по каждому направлению. Такой режим "короткогозамыкания" наблюдается при диффузии плазмы, ограниченной металлич. стенками. При этом электроны уходят из плазмы вдоль В, ионы - поперёк В,и по плазме протекает ток, к-рый замыкается через проводящие стенки камеры. Характерное время такой диффузии 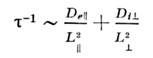может быть на порядки меньше амбиполярного. В неограниченной плазме возмущениееё концентрации приводит к появлению вихревого тока, к-рый определяет диффузионнуюэволюцию неоднородности. На рис. 1 приведены поверхности пост. концентрациипри диффузии малого (точечного) возмущения в однородной неограниченнойплазме. Характерные размеры возмущённой области вдоль и поперёк В определяютсянаиб. подвижными в каждом направлении частицами и равны соответственно

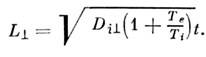
Для выбранного на рис. 1 примера отношение 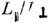равно 10. Поляризац. электрич. поле вызывает протекание электронного иионного токов по фоновой плазме, поддерживающих квазинейтральность и формирующихобласть с пониж. концентрацией плазмы (заштрихована на рис. 1). Скоростьамбиполярного дрейфа в магн. поле отлична от нуля даже в простой слабоионизов. плазме. Поэтому при протекании внеш. тока через неоднородность эволюцияеё сопровождается движением и нелинейной деформацией профиля, образованиемскачков и разделением неоднородности на движущиеся с разной скоростью сгусткиплазмы.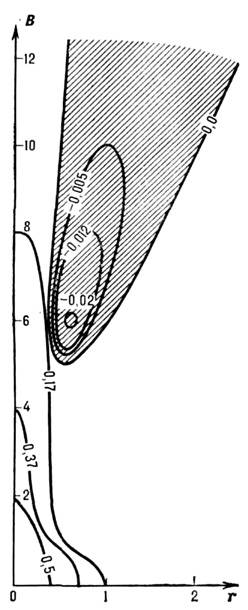

Рис. 1. Линии равной концентрации при диффузииточечного возмущения в однородной неограниченной плазме. Размеры областивозмущения вдоль поля в 10 раз больше области возмущения поперёк поля.

П. п. в полностью ионизованной плазмев однородном магнитном поле. Неоднородная плазма разлетается вдольВ со скоростью ионно-звуковых волн ~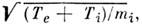поэтому не существует диффузии простой, полностью ионизованной плазмы вдольВ, реализуется только диффузия поперёк поля, определяемая электронами 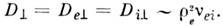Подвижности компонент также отсутствуют - определена только суммарная проводимость. Оценки для температуропроводности такие же, как и в слабоионизов. плазме, т. е.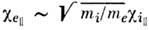при Т _е~ Т _i. В сильном магн. поле поперечноек В электрич. поле с точностью до 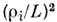не приводит к току, а вызывает дрейф всей плазмы в целом со скоростью с[ЕВ]/В ² (см.Дрейф заряженных частиц). В полностью ионизованной плазме имеютсятакже т. н. косые (описываемые недиагональными элементами тензора) потокичастиц поперёк В (рис. 2):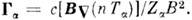В прямом однородном магн. поле их дивергенция равна нулю 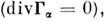т. к. они не связаны с перемещением ведущих центров ларморовских орбит, а обусловлены неполной компенсацией потоков электронов и ионов из-за неоднородногораспределения их орбит. В неоднородном магн. поле 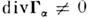из-за дрейфа ведущих центров связанного с неоднородностью и кривизной магн. поля.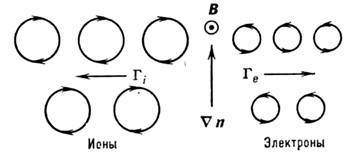

Рис. 2. Потоки частиц в неоднородной плазмепоперёк магнитного поля.

"Косые" потоки электронов и ионов, проявляющиесякак диамагн. ток, приводят к появлению силы трения электронов об ионы R= m_ev_ei (Г _е - Г _i).Дрейфовое движение электронов и ионов поперёк В под действиемэтой силы происходит совместно в направлении против 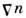со скоростью ~ c[BR]/e²B². ипроявляется как амбиполярная диффузпя с коэф.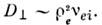Того же пооядка поперечные диагональные коэф. термодиффузии 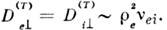Перенос ионов примеси происходит значительно быстрее, т. к. он обусловленионно-ионными столкновениями и не связан с переносом электронов. Даже приоднородной темп-ре он не сводится к диффузии, поскольку поток примеси содержитслагаемые, иропорц. как градиенту её концентрации, так и градиенту концентрацииосн. компоненты.
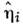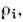
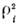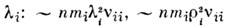Перенос импульса (вязкость) в полностьюионизованной плазме определяется ионами. Тензор вязкости в магн. тюле имеет элементы, пропорц. ларморовскому радиусу и и ~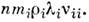Вязкость и инерция ионов приводят к дополнительному по сравнению с диффузионнымпотоку ионов. Условие обращения его в нуль определяет поперечное к В амбиполярноеэлектрич. поле.
Перенос тепла не связан условием квазинейтральностии происходит, вообще говоря, быстрее, чем перенос частиц. Напр., поперечная(диагональная) теплопроводность полностью ионизованной плазмы определяетсяионами: коэф. температуропроводности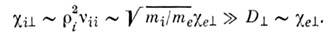

Классич. описание П. п. возможно при оченьмалом смещении частиц между столкновениями (малой длине свободного пробега).В полностью ионизованной плазме, где сечения столкновений падают с ростомскорости, для описания быстрых электронов, у к-рых длина пробега велика, необходим кинетич. подход, учитывающий, что электроны, ускоряемые электрич. полем между столкновениями, могут приобрести такую скорость, что они ужеперестанут тормозиться за счёт столкновений. С др. стороны, даже в слабостолкновит. плазме с достаточно плавными ф-циями распределения, к-рые можно характеризоватьанизотропными темп-рами, потоки пропорциональны градиентам макроскопич. параметров, что даёт возможность построить замкнутую систему ур-ний переноса.

Неоклассические П. п. в неоднородноммагнитном поле. Все диагональные коэф. переноса поперёк В спадают с ростом . как В ^-2. На этом основаноудержание плазмы в магнитных ловушках. Однако из-за криволинейностии неоднородности магн. поля П. п. в них оказываются сложнее. Дрейфы заряж. частиц в неоднородном магн. поле приводят к поляризации плазмы и к течениюеё в скрещенных электрич. и магн. полях. Поэтому П. п. поперёк магн. поверхностейв гидродинамич. приближении, напр., носят характер своеобразной конвекции. В этом режиме эфф. неоклассич. коэф. температуропроводности (рис. 3,III)и диффузии в токамаке в 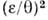раз больше, чем в прямом цилиндре (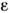= r/R - отношение малого и большого радиусов магн. поверхности,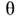- отношение полоидального и тороидального магн. полей).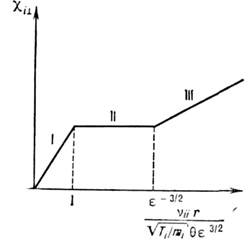

Рис. 3. Зависимость неоклассической ионнойтемпературопроводности от частоты столкновений в токамаке: I - режим редкихстолкновений ("банановый"); II - режим плато; III - гидродинамический режим.

В режиме редких столкновений (рис. 3, I)смещение частиц поперёк В между столкновениями может намногопревышать ларморовский радиус. При этом осн. вклад в радиальный неоклассич. перенос дают частицы с малыми продольными скоростями, запертые из-за неоднородностиполя В на внеш. обводе тора. Проекции их траекторий на плоскостьмалого сечения тора имеют вид бананов шириной 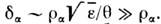При столкновении такие частицы смещаются на большое расстояние (порядка 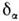)и эфф. частота столкновений для них высока, поэтому, несмотря на малочисленность, именно они определяют П. п.: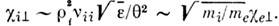Диффузия автоматически амбиполярна;В промежуточном режиме (плато II на рис. 3) коэф. переноса тоже определяютсячастицами с малыми продольными скоростями и не зависят от частоты столкновений. Неоклассич. П. п. существенны также в др. магн. ловушках - стеллараторах, открытых ловушках.

Аномальные П. п. Применимость представленийо классических (столкновительных) П. п. ограничена тем, что в неоднороднойплазме, особенно в магн. поле, возможны многочисл. неустойчивости. В результатеих развития плазма может перейти в турбулентное состояние. Возникающиепри этом хаотич. электрич. и магн. поля в ряде случаев приводят к аномальнымП. п., на порядки превышающим классические. Макроскопич. потоки частиц, импульса и энергии при этом определяются не только средними полями и профилями, но и установившимися уровнем и спектром колебаний. Аномальную диффузиючастиц сравнивают с Бома диффузией, к-рая наблюдалась в газовыхразрядах. Перенос частиц и электронный теплоперенос в токамаках такжеаномальны и значительно превышают неоклассич. значения, но оказываютсяменьше бомовских. Как правило, не удаётся построить замкнутую систему ур-ний, описывающую аномальные П. п.; результаты в осн. сводятся к полуколичеств. оценкам. Исключение составляет случай слабой турбулентности, когдав квазилинейном приближении удаётся описать аномальные П. п. Построениеобщей количеств. теории аномальных П. п. является одной из наиб. актуальныхзадач физики плазмы.

Лит.: Галеев А. А., Сагдеев Р. 3.,"Неоклассическая" теория диффузии, в сб.: Вопросы теории плазмы, в. 7,М., 1973; Xинтон Ф., Явления переноса в столкновительной плазме, пер. сангл., в кн.: Основы физики плазмы, т. 1, М., 1983; Xортон В., Дрейфоваятурбулентность и аномальный перенос, пер. с англ., в кн.: Основы физикиплазмы, т. 2, М., 1984; Ораевский В. Н., Коников Ю. В., Xазанов Г. В.,Процессы переноса в анизотропной околоземной плазме, М., 1985; РожанскийВ. А., Цендин Л. Д., Столкновительный перенос в частично ионизованной плазме, М., 1988.

В. А. Рожанский, Л. Д. Цендин.