- РАСПРЕДЕЛЕНИЕ
-
- осн. понятие вероятностей теории и матем. статистики. Р. полностью характеризует случайную величину. Пусть x- дискретная случайная величина, принимающая (конечное или бесконечное) счётное множество значений {xn}. Если вероятность реализации значения х п равна Р п, т. е. Р(х= х п)= Р п, то множество значений вероятностей Р п наз. дискретным Р. вероятности. Вероятности Р п удовлетворяют условиям
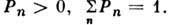 Предположим, что вероятность рассеяния частицы на мишени равна р. Тогда регистрируемое число рассеянных частиц n- дискретная случайная величина, Р. к-рой является биномиальным распределением:
Предположим, что вероятность рассеяния частицы на мишени равна р. Тогда регистрируемое число рассеянных частиц n- дискретная случайная величина, Р. к-рой является биномиальным распределением: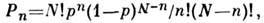
где N- число частиц, брошенных на мишень.
Пусть теперь x- непрерывная случайная величина, принимающая любое значение из интервала [xmin, xmax]. Если вероятность реализации значения
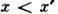 равна
равна 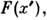 т. е.
т. е. 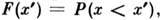 то F(x) наз. ф-цией распределения, a f(x), определяемая равенством
то F(x) наз. ф-цией распределения, a f(x), определяемая равенством 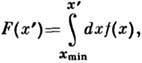
наз. ф-цией плотности вероятности или просто Р. Из определения F(x )следует, что
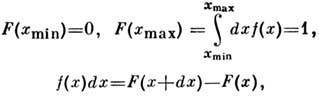
т. е. f(x )имеет смысл плотности вероятности на единицу длины. Примером непрерывного Р. является Максвелла распределение по скоростям ux, uy, uz частиц макроскопич. системы, находящейся в статистич. равновесии:
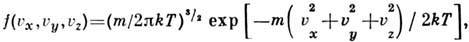
где т- масса частицы, Т- абс. темп-pa. Это Р. является частным случаем многомерного Гаусса распределения.
Наряду с ф-цией плотности вероятности часто используют её фурье-преобразование, наз. характеристической функциейF случайной величины; для дискретной величины
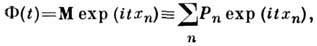
для непрерывной величины
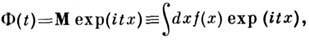
где М - матем. ожидание. Характеристич. ф-ция полностью определяет Р. случайной величины и часто является более удобным средством её описания. Для дискретной случайной величины х п с помощью замены Z= exp(it) часто переходят от характеристич. ф-ции к производящей ф-ции (см. Производящий функционал):
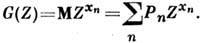
Др. способом описания случайной величины является задание её моментов
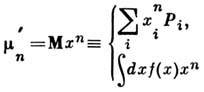
или центральных моментов
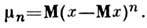
При довольно общих предположениях набор моментов полностью определяет Р. Приведём нек-рые Р., часто используемые в физике и матем. статистике (см. также Коши распределение, Полиномиальное распределение, Пуассона распределение, Устойчивые распределения). Отрицательное биномиальное распределение (распределение Паскаля). Это Р. даёт вероятность затраты r попыток для достижения т успешных попыток. Если p- вероятность успешной попытки, то вероятность r равна
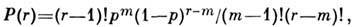
ср. значение
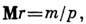
дисперсия
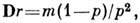
производящая ф-ция
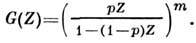
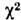 -распределение. Пусть yi - независимые случайные величины, подчиняющиеся нормальному Р. с нулевым ср. значением и единичной дисперсией, и пусть
-распределение. Пусть yi - независимые случайные величины, подчиняющиеся нормальному Р. с нулевым ср. значением и единичной дисперсией, и пусть 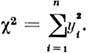
Тогда ф-ция плотности вероятности
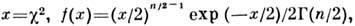
ср. значение
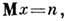
дисперсия
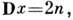
характеристич. ф-ция
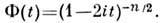
Величину n наз. числом степеней свободы. Если х п и х т имеют независимые c2 -распределения с n и m степенями свободы соответственно, то сумма х (k) = = x(n)+x(m). имеет c2-pacпpeдeлeниe с k = n + m степенями свободы. При n > 30 c2 -распределение близко к нормальному с теми же ср. значением и дисперсией. Если независимые величины у i принадлежат нормальному Р. со средними mi и единичными дисперсиями, то x имеет нецентральное c2 -распределение с n степенями свободы, к-рое обозначают c2(n, D), где
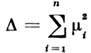 - параметр нецентральности. Характеристич. ф-ция
- параметр нецентральности. Характеристич. ф-ция 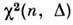 равна
равна 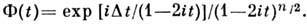
c2 -распределение находит широкое применение в проверке статистических гипотез.
Распределение Стьюдента, t-pacпpeделение. Пусть у i, i =1, ..., n- случайные величины, имеющие нормальные Р. со средним m и дисперсией s2, тогда величина
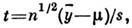
где
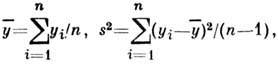
подчиняется распределению Стьюдента с ф-цией плотности вероятности
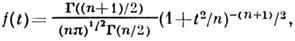
ср. значением
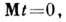
дисперсией
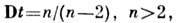
моментами
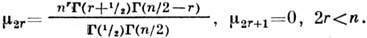
При n: , распределение Стьюдента приближается к нормальному Р. с нулевым средним и единичной дисперсией. С его помощью можно вычислить доверительные интервалы, для m и статистические критерии проверки гипотез.
Экспоненциальное распределение. Пусть c- положит. случайная величина, l - положит. параметр, ф-ция плотности вероятности экспоненциального Р.
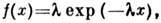
ср. значение
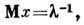
дисперсия
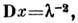
характеристич. ф-ция

Экспоненциальному Р. подчиняется, напр., время жизни радиоакт. ядер.
Гамма-распределение. Пусть c - положит. случайная величина, а, b- положит. параметры, ф-ция плотности вероятности гамма-распределения равна
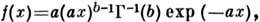
ср. значение
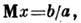
дисперсия
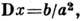
характеристич. ф-ция
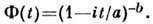
При b =1 гамма-распределение совпадает с экспоненциальным Р., а при b = n/2, a = 1/2 - с c2 -распреде-лением с n степенями свободы.
Логарифмически нормальное распределение. Пусть x- положит. случайная величина, логарифм к-рой отвечает нормальному Р. со средним m и дисперсией s2, тогда ф-ция плотности вероятности
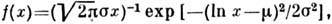
ср. значение
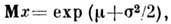
дисперсия
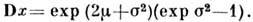
Лит.:Fеллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 3 изд., т. 1-2, М., 1984; Прохоров Ю. В., Pозанов Ю. А., Теория вероятностей, 2 изд., М., 1973; Статистические методы в экспериментальной физике, пер. с англ., М., 1976; Справочник по теории вероятностей и математической статистике, 2 изд., М., 1985; Боровков А. А., Математическая статистика, М., 1984. В. П. Жигунов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.