Akademik

(от англ. spin - вращаться) - элемент пространства спинорного представления группы вращений. Вращений группа SO(n )при п 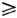3 двусвязна. Её односвязная накрывающая называется спинорной группойSpin(n). Каждое линейное представление SO(n )порождает представлениеSpin(n); однако часть линейных представлений Spin ( п )порождаетсядвузначными (проективными с мультипликатором ±1) представлениями SO(n)- её спинорными представлениями. Простейшее спинорное представлениеимеет размерность 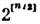(где [...] - символ целой части числа) и реализуется в Клиффорда алгебреК _п степени 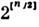. Оно неприводимо для нечётных п и разлагается в сумму двух неэквивалентныхпредставлений одинаковой размерности для чётных п.

Существуют два типа С.: С., связанные с группой SO(n) - группойвращений n -мерного евклидова пространства, и С., связанные с группой SO(p, q) (p + g= п) - группой «вращений» псевдоевклидовапространства 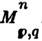, сохраняющих квадратичную форму: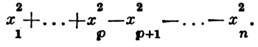

В физике наиб. употребительны С. в пространстве R³ [С. группы SO(3)] (нерелятивистская квантовая механика) и в пространствеМинковского (С. собственной Лоренца группы в релятивистской 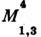теории).

Спинор в R³. Простейшее спинорное представление (спинорноепредставление ранга 1) двумерно [т. к. Spin (1) ~ SU(2)]. С. ранга1 характеризуется парой (комплексных) чисел 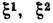. При повороте на угол вокруг оси с направляющим единичным вектором n = (n_l,n₂, n₃) С. ранга 1 преобразуется по ф-ле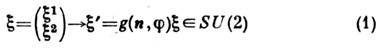

с помощью матрицы

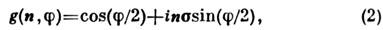
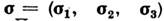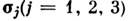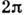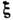где , -Паули матрицы. При повороте на угол С. переходитв -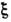, что свидетельствуето неопределённости знака С., т. е. о двузначности представления. Выражение(2) задаёт представление SO(3), как следует из коммутац. соотношенийдля матриц Паули. В этом представлении матрица 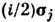является генератором поворота вокруг оси j. Преобразование (1) сохраняетбилинейную форму 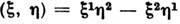, определённую на двумерных векторах (контравариантных)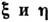.Это позволяет ввести в линейном пространстве таких векторов кососимметрическую«метрику»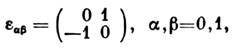

и ковариантные С.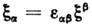, преобразующиеся с помощью эрмитово сопряжённой матрицы 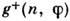.Тогда билинейная форма естественно интерпретируется как скалярное произведение: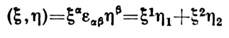

(по повторяющимся индексам подразумевается суммирование).

В качестве базиса в пространстве С. ранга 1 можно выбрать собств. векторы

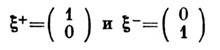
матриц 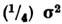и 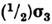, допускающихестеств. интерпретацию квадрата вектора епина и его z-проекции; собств. значениями будут ³/₄ = ¹/₂(1+ ¹/₂) и 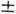¹/₂ соответственно. Поэтому С. ранга 1 описывают частицы со спином ¹/₂.

С. старших рангов строятся по аналогии с теорией тензоров. Контравариантнымспинором ранга r наз. набор У (комплексных) чисел , преобразующихся по закону: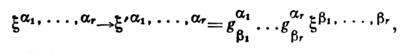

где 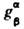-элементы матрицы 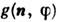. В алгебре С. можно ввести операции, аналогичные операциям в тензорнойалгебре: поднятие и опускание индексов, свёртка и т. д. С.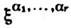ранга г наз. симметрическим, если его компоненты не меняются при любойперестановке индексов. В пространстве симметрических С. реализуются всенеприводимые представления группы вращений веса l, 2l = r.

Спинор в М ⁴. Два простейших неприводимых (полу-спинорных)представления SO(3,1) двумерны и обозначаются столбцам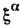и и 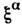соответственнос непунктирными и с пунктирными индексами. При пространственных поворотах 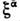преобразуются (как и С. в R³) с помощью матрицы (2), а при специальных Лоренца преобразованиях - гиперболич. поворотах на угол 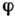в плоскости (x₀, п) - с помощью матрицы h: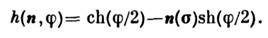

Пунктирные С.,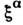,преобразуются с помощью комплексно сопряжённых матриц g* и h* соответственно. Кососимметрическая матрица 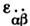позволяет определить компоненты пунктирных С. При пространственной инверсии 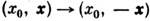пунктирный и непунктирный С. переходят друг в друга:,

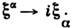Включение инверсий означает переход от собств.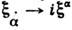группы Лоренца SO(3, 1) к группе Лоренца О(3, 1). Поэтомупростейшее спинорное представление O(3, 1) четырёхмерно и образовано биспинором 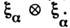( - знактензорного произведения), обычно записываемым в виде столбца: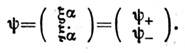

Инвариантные и ковариантные билинейные формы в пространстве биспиноровстроятся с помощью Дирака матриц 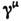,,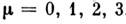 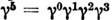иопределения дираковского сопряжения 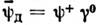(«+» означает эрмитово сопряжение). Так, формы 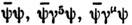-есть соответственно скаляр, псевдоскаляр и 4-вектор относительно преобразованийиз 0(3, 1).

Помимо дираковского вводят майорановское сопряжение 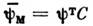(Т - означает транспонирование), где С- матрица зарядового сопряжения. Майорановским С. наз. С., для к-рого 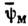пропорционален y _д (множитель пропорциональности зависитот представления матриц Дирака); в частности, в майо-рановском представлении(где 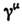и 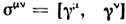вещественны)компоненты майорановского C. вещественны.

Вейлевским С. наз. С., удовлетворяющий соотношению 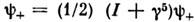или 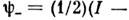-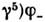,где I - единичная матрица (соответственно правый и левый С.). Числоего компонент также вдвое меньше обычного; он используется в теориях с киральной симметрией.

В пространстве биспиноров можно задать линейное релятивистски инвариантноеур-ние, описывающее частицы со спином ¹/₂ (спинорныечастицы), с ненулевой массой - Дирака уравнение, с нулевой массой- Вейля уравнение.

С., связанные с многомерными пространствами, находят применение в теории тяготения, Калуцы - Клейна теории, теории суперструн и т. д. Многообещающиеприменения теории С. связаны с теорией твисторов.

Спинорные многообразия. Глобально спинорное поле можно задать не налюбом многомерном пространстве. Существование таких пространств (спинорныхмногообразий, см. Расслоение )определяется топологич. инвариантами.

Первые упоминания двузначной природы группы вращений восходят к Л. Эйлеру(L. Euler) (параметризации группы вращений углами Эйлера). В работах О. Родригеса (О. Rodrigues), У. Гамильтона (W. Hamilton), А. Кэли (A. Cayley),У. Клиффорда (W. Clifford) и др. были получены важные результаты, нашедшиеестеств. продолжение в рамках теории С. Построение спинорных представленийв инфинитезимальной форме проведено Э. Картаном (Е. Cartan, 1913). Дальнейшееразвитие теории С. инициировалось открытием спина электрона (1925) и появлениемур-ний П. Дирака (P. Dirac) и Г. Вейля (H. Weyl). Спинорное исчислениебыло построено в работах Б. Ван-дер-Вардена (В. van der Waerden) и др. Термин «С.» предложен П. Эренфестом (P. Ehrenfest, 1929).

Лит.: Ландау Л. Д., Л и ф ш и ц Е. М., Квантовая механика, 4изд., М., 1989; Г е л ь ф а н д И. М., М и н л о с Р. А., Шапиро 3. Я.,Представления группы вращении и группы Лоренца и их применения, М., 1958;Ван дер Варден Б., Принцип запрета и спин, в кн.: Теоретическая физика20 века, М., 1962; Берестецкий В. Б., Л и ф ш и ц Е. М., Питаевский Л. П., Релятивистская квантовая теория, ч. 1, М., 1968; Дирак П., Спинорыв гильбертовом пространстве, пер. с англ., М., 1978; Пенроуз Р., РиндлерВ., Спиноры и пространство-время, пер. с англ., [т. 1], М., 1987; [т. 2]- Спиноры и пространство-время. Спинорные и твисторные методы в геометриипространства-времени, пер. с англ., М., 1988; Budinich P., Trautman A.,The spinorial chessboard. Springer, N. Y., 1988. М. И. Монастырский.