Akademik

- линейный оператор U, отображающий предгильбертово пространство (в частности, гильбертово пространство) X в предгильбертово пространство Y и сохраняющий нормы (или длины векторов). Линейный оператор унитарен тогда и только тогда, когда ( х, y) = (Ux, Uy )для всех 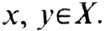Наиболее важный случай У. о.- отображение гильбертова пространства в себя, то есть унитарные преобразования. Характеристическими признаками унитарности линейного оператора 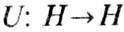являются: 1) 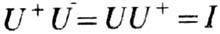(I -тождественное преобразование), т. 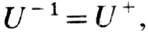е. где 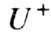-сопряжённый оператор; 2) спектр оператора лежит на единичной окружности, и имеет место спектральное разложение

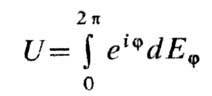
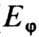( -спектральная ф-ция). Совокупность У. о., действующих в H, образует группу. Всякая сильно непрерывная однопараметрич. группа У. о. представляется в виде

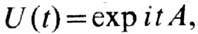где А - самосопряжённый оператор. Примером У. о. и его обратного в пространстве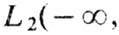 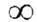) являются взаимно обратные Фурье преобразования.

В. И. Соболев.