Akademik

ДИСПЕРСИЯ ЗВУКА

ДИСПЕРСИЯ ЗВУКА: (дисперсия скорости звука), зависимость фазовой скорости гармонич. звук. волн от их частоты. Д. з. может быть обусловлена как физ. св-вами среды, так и присутствием в ней посторонних включений и наличием границ тела, в к-ром авук. волна распространяется. Д. з., связанная с физ. св-вами среды, возникает, когда воздействие акустич. волны приводит к неравновесному состоянию среды, возбуждая её внутр. степени свободы (колебат. и вращат. движения молекул), процессы ионизации и диссоциации молекул, хим. реакции, перестройку структуры жидкости, процессы взаимодействия ультразвука с электронами проводимости в металлах и ПП, магнитоупругие явления и т. д. Выравнивание энергии между поступат. и внутр. степенями свободы происходит за нек-рое время, наз. временем релаксации tр (см. РЕЛАКСАЦИЯ АКУСТИЧЕСКАЯ). Если период Т звук. волны мал по сравнению с tр (высокие частоты), то за время Т-tp внутр. степени свободы не успевают возбудиться, поэтому среда будет вести себя так, как будто внутр. степени свободы отсутствуют. Если же 7->tр (низкие частоты), то часть энергии поступат. движения успеет перераспределиться на внутр. степени свободы. При этом, вследствие уменьшения энергии поступат. движения, упругость среды и скорость звука также будут меньше, чем в случае высоких частот. Т. о., при наличии релаксации скорость звука увеличивается с ростом частоты (рис.).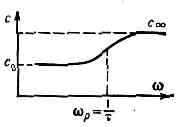

Быстрее всего рост скорости происходит при частотах, близких к частоте релаксации wр=1/t (дисперс. область). Для большинства сред wр лежит в области УЗ и гиперзвуковых частот. Если с0 — скорость звука при малых частотах (wt-1), а c? — при очень больших (wt->1), то скорость звука для произвольной частоты со описывается ф-лой:

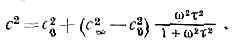Такая зависимость с (w) характерна для всех релаксац. процессов в однородных средах. Д. з. сопровождается также повышенным поглощением звука сравнительно с поглощением, обусловленным сдвиговой вязкостью и теплопроводностью.

Д. з. в газах связана с возбуждением колебат. и вращат. степеней свободы молекул, а в жидкостях — с колебательной и поворотно-изомерной релаксациями и перестройкой внутр. структуры жидкости, а также с процессами диссоциации, хим. реакциями и т. д. В тв. телах Д. з. обычно появляется, когда акустич. волна взаимодействует с к.-л. видами внутр. возбуждений, и под её воздействием происходит изменение состояния эл-нов проводимости, системы спинов, спиновых волн и др.

Величина Д. з., определяемая как D=(с?-c0)/c0, может сильно различаться для разных в-в. Так, напр., в углекислом газе D»4%, в бензоле D»10%, в морской воде D0,01, а в очень вязких жидкостях и в высокополимерных соединениях скорость звука может изменяться на десятки процентов. Частотный диапазон, в к-ром имеет место Д. з., также различен для разных в-в. Так, в углекислом газе при нормальном давлении и темп-ре 18°С wр=28 кГц, в морской воде wр=120 кГц. В четырёххлористом углероде, бензоле, хлороформе и др. область релаксации попадает в область частот =109— —1010 Гц.

К Д. з. того же типа, но не носящей релаксац. хар-ра, приводят теплопроводность и вязкость среды. Эти виды Д. з. обусловлены обменом энергией между областями сжатий и разрежений в звук. волне и особенно существенны для микронеоднородных сред. Д. з. может проявляться также в среде с вкрапленными неоднородностями (резонаторами), напр. в воде, содержащей пузырьки газа. В этом случае при частоте звука, близкой к резонансной частоте пузырьков, часть энергии звук. волны идёт на возбуждение колебаний пузырьков, что приводит к Д. з. и к возрастанию поглощения звука.

Как правило, Д. з. лгала, за исключением нек-рых спец. случаев, таких, как неоднородная среда (напр., пузырьки газа в воде) или очень высокие частоты.

Принципиально другим типом Д. з. явл. «геометрическая» дисперсия, обусловленная наличием границ тела или среды. Она появляется при распространении волн в стержнях, пластинах, в любых волноводах акустических. Для изгибных волн Д. з. наблюдается в тонких пластинах и стержнях (их толщина должна быть много меньше, чем длина волны). При изгибании тонкого стержня упругость на изгиб тем больше, чем меньше изгибаемый участок. При распространении изгибной волны длина изгибаемого участка определяется длиной волны звука. Поэтому с уменьшением длины волны (с повышением частоты) увеличивается упругость, а следовательно, и скорость распространения волны. Фазовая скорость такой волны пропорц. ?w.

При распространении звука в волноводах звук. поле можно представить как суперпозицию нормальных волн, фазовые скорости к-рых для прямоугольного волновода с жёсткими стенками определяются соотношением:

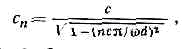где n=1, 2, 3, . . .— номер нормальной волны, с — скорость звука в свободном пр-ве, d — поперечный размер волновода. Фазовая скорость нормальной волны всегда больше скорости звука в свободной среде и уменьшается с ростом частоты.

Д. з. обоих типов приводит к расплыванию формы звук. импульса при его распространении. Это особенно важно для гидроакустики, атмосферной акустики и геоакустики, где имеют дело с распространением звука на большие расстояния, а также для УЗ линий задержки.