équipollence [ ekɥipɔlɑ̃s ] n. f.
• 1265; lat. æquipollentia « équivalence »
1 ♦ Vx Équivalence.
2 ♦ Mod. Math. Propriété de deux bipoints équipollents.
● équipollence nom féminin (bas latin aequipollentia, équivalence) Relation d'équivalence ∼ définie sur l'ensemble des bipoints d'un espace affine par (M,N) ∼ (M′, N′) si et seulement si MN′ et M′N ont même milieu. [Si (M,N) ∼ (M′,N′), alors (M, M′) ∼ (N, N′). Chaque classe d'équivalence est un vecteur ; la classe de (M, N) est notée
.]
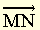⇒ÉQUIPOLLENCE, subst. fém.
Fait d'être équipollent.
A.— Vx. [Correspond à équipollent A] Et ce n'est pas leurs lois [de nos maîtres charnels] et leurs équipollences Qui feront notre loi quand nous serons jugés (PÉGUY, Ève, 1913, p. 875).
B.— En partic.
1. LOG. [Correspond à équipollent B 1] ,,L'équipollence des propositions. Propriété des propositions qui reviennent, qui équivalent l'une à l'autre`` (Ac.).
2. MATH. [Correspond à équipollent B 2] :
• La représentation géométrique des nombres complexes est à l'origine des travaux de Bellavitis qui, entrepris à partir de 1832, le conduiront à sa « théorie des équipollences », première présentation d'ensemble d'un calcul sur les grandeurs dirigées.
Hist. gén. sc., t. 3, vol. 1, 1961, p. 18.
Prononc. et Orth. :[
]. Cf. équi-. [ll] notés ds FÉR. 1768, FÉR. Crit. t. 2 1787, LAND. 1834, GATTEL 1841, NOD. 1844, BESCH. 1845. Ds DG on admet la prononc. avec [ll] à côté de celle usuelle avec [l]. Le mot est attesté ds Ac. 1718, s.v. équipolence. Ds Ac. 1740-1932 avec 2 l. À comparer avec équipo(l)lé. Étymol. et Hist. 1275-80 equipollences (J. DE MEUN, Rose, éd. F. Lecoy, 11750). Empr. au b. lat. aequipollentia « équivalence ». Fréq. abs. littér. :3.
]. Cf. équi-. [ll] notés ds FÉR. 1768, FÉR. Crit. t. 2 1787, LAND. 1834, GATTEL 1841, NOD. 1844, BESCH. 1845. Ds DG on admet la prononc. avec [ll] à côté de celle usuelle avec [l]. Le mot est attesté ds Ac. 1718, s.v. équipolence. Ds Ac. 1740-1932 avec 2 l. À comparer avec équipo(l)lé. Étymol. et Hist. 1275-80 equipollences (J. DE MEUN, Rose, éd. F. Lecoy, 11750). Empr. au b. lat. aequipollentia « équivalence ». Fréq. abs. littér. :3.
équipollence [ekɥipɔlɑ̃s] n. f.
ÉTYM. V. 1265, equipollence; lat. æquipollentia « équivalence », de æquipollens. → Équipollent.
❖
1 Vx. Égalité de valeur, de force. ⇒ Équivalence. — Spécialt. Log. || Équipollence de deux propositions.
0 Il y a trois choses à considérer dans la proposition : l'opposition, l'équipollence et la conversion.
2 (XXe). Mod. Math. Caractère de deux bipoints équipollents. || L'équipollence est une relation d'équivalence, définie sur l'ensemble des bipoints d'un espace affine; elle permet de construire un espace vectoriel à partir d'un espace affine, les vecteurs y étant définis comme des classes d'équivalence de la relation d'équipollence.
Encyclopédie Universelle. 2012.