- раздел алгебры, изучающий объекты, в к-рых, наряду с операциями сложения и умножения, имеются операции дифференцирования: дифференциальные кольца, дифференциальные модули, дифференциальные поля, дифференциальные алгебраич. многообразия.
Один из основных объектов Д. а.- алгебра дифференциальных полиномов 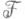 {Y1: ..., Yn}, являющаяся аналогом кольца многочленов в коммутативной алгебре (см. Расширение дифференциального поля). Каждой системе дифференциальных уравнений
{Y1: ..., Yn}, являющаяся аналогом кольца многочленов в коммутативной алгебре (см. Расширение дифференциального поля). Каждой системе дифференциальных уравнений

ставится в соответствие совершенный дифференциальный идеал {F1,. .., Fk}, порожденный этой системой в алгебре дифференциальных полиномов. Теорема Ритта - Рауденбаха о базисе утверждает, что таким образом получаются все совершенные дифференциальные идеалы (дифференциальный идеал I наз. совершенным, если из  для нек-рого n>0 следует, что
для нек-рого n>0 следует, что  ), т. е. в любом из них можно выбрать конечное число дифференциальных полиномов таких, что совершенный дифференциальный идеал, порожденный этими полиномами, совпадает с данным. В отличие от теоремы Гильберта о базисе в кольце многочленов, в теореме Ритта - Рауденбаха существенна совершенность идеалов, т. е. дифференциальный идеал (даже совершенный) может не являться конечно порожденным дифференциальным модулем.
), т. е. в любом из них можно выбрать конечное число дифференциальных полиномов таких, что совершенный дифференциальный идеал, порожденный этими полиномами, совпадает с данным. В отличие от теоремы Гильберта о базисе в кольце многочленов, в теореме Ритта - Рауденбаха существенна совершенность идеалов, т. е. дифференциальный идеал (даже совершенный) может не являться конечно порожденным дифференциальным модулем.
Совершенному дифференциальному идеалу ставится в соответствие дифференциальное алгебраич. многообразие - множество точек в аффинном пространстве над нек-рым универсальным расширением поля коэффициентов, аннулирующих любой полином из данного идеала. Имеет место аналог теоремы Гильберта о нулях. Пусть F1, ..., F р- конечная система дифференциальных полиномов и пусть G- дифференциальный полином, обращающийся в нуль во всех решениях данной системы. Тогда некоторая степень полинома Gявляется линейной комбинацией полиномов Fи их производных разного порядка с коэффициентами из алгебры дифференциальных полиномов. В частности, если система F1,. . ., Fp не имеет нулей, то нек-рая линейная комбинация полиномов Fи их производных разного порядка равна единице.
Совершенный дифференциальный идеал допускает представление в виде пересечения конечного числа простых дифференциальных идеалов. Этому представлению соответствует разложение многообразия на конечное число неприводимых компонент. Для простых дифференциальных идеалов вводится понятие общего нуля и его размерности, как н в алгебраич. геометрии. Для неприводимого замкнутого множества Vв дифференциальном аффинном пространстве, т. е. в аффинном пространстве над универсальным расширением Uполя коэффициентов, определяется дифференциальный размерностный полином 
где т- количество дифференцирований в поле F. Коэффициент а т наз. дифференциальной размерностью множества V, степень полинома t= deg coy - дифференциальным типом множества V, а коэффициент а t.- его типичной дифференциальной размерностью. Полином wV является бирациональным инвариантом, но не является дифференциальным бирациональным инвариантом. Таковыми будут am(V), r(V)и at(V)(V). Нахождение дифференциальных бирациональных инвариантов представляет значительный интерес. Другая проблема - оценить возможные значения полученных инвариантов. Пусть 2 - подмножество в  {Y1, ..., Yn}. Если элементы из 2 имеют ограниченный порядок, то дифференциальные размерностные полиномы компонент {2 } подчинены некоторым ограничениям. В частности, если для каждого Yj порядок относительно Yj любого элемента из е не превосходит ej, то для любой компоненты многообразия {2 } из условия а m (р) = О следует, что
{Y1, ..., Yn}. Если элементы из 2 имеют ограниченный порядок, то дифференциальные размерностные полиномы компонент {2 } подчинены некоторым ограничениям. В частности, если для каждого Yj порядок относительно Yj любого элемента из е не превосходит ej, то для любой компоненты многообразия {2 } из условия а m (р) = О следует, что  В общем случав имеется гипотеза, что
В общем случав имеется гипотеза, что

Если множество  состоит из пдифференциальных полиномов F1,..., Fn, то выдвигаются еще две гипотезы. Пусть
состоит из пдифференциальных полиномов F1,..., Fn, то выдвигаются еще две гипотезы. Пусть
и 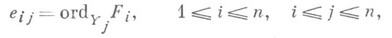

где p пробегает симметрич. группу S п. Первая гипотеза утверждает, что для любой компоненты р многообразия {Fx, ..., Fn} изam(p) = 0 следует, что am-1( )
)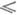 h. Это предположение доказано в нек-рых частных случаях. Вторая гипотеза состоит в том, что для любой компоненты р многообразия {F1, ..., Fn} из а т (р)=am_1(
h. Это предположение доказано в нек-рых частных случаях. Вторая гипотеза состоит в том, что для любой компоненты р многообразия {F1, ..., Fn} из а т (р)=am_1( ) = 0 следует, что w р = 0.
) = 0 следует, что w р = 0.
продолжение Дифференциальная алгебра...
Одной из сложных проблем, исследуемых Д. а., является проблема разложения дифференциально алгебраич. многообразия на неприводимые компоненты. Даже если система 2 состоит из одного неприводимого дифференциального полинома s, то соответствующее многообразие состоит, в общем случае, из нескольких компонент, одна из к-рых содержит все неособые решения уравнения s=0 (хотя может содержать и особые решения), а все остальные компоненты состоят из решений, обращающих в 0 любую сепаранту дифференциального полинома а. Случай гиперповерхности (система 2 из одного уравнения) особенно важен, т. к. всякое дифференциально алгебраич. многообразие над обыкновенным дифференциальным полем дифференциально бирационально изоморфно гиперповерхности.
Поскольку всякий простой дифференциальный идеал полностью определяется своим характеристич. множеством, проблему разложения дифференциально алгебраического многообразия { } можно разделить на две: 1) найти конечное множество
} можно разделить на две: 1) найти конечное множество  авторедуцированных подмножеств в
авторедуцированных подмножеств в 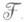 {Y1, ...,Yn), каждое из к-рых является характеристич. множеством простого дифференциального идеала, содержащего Ф, такое, что U включает в себя характеристич. множество каждой компоненты {Ф}; 2) для данного авторедуцированного множества в
{Y1, ...,Yn), каждое из к-рых является характеристич. множеством простого дифференциального идеала, содержащего Ф, такое, что U включает в себя характеристич. множество каждой компоненты {Ф}; 2) для данного авторедуцированного множества в  {Y1,. . ., Y п} определить, является ли оно характеристич. множеством какой-нибудь компоненты {Ф}.
{Y1,. . ., Y п} определить, является ли оно характеристич. множеством какой-нибудь компоненты {Ф}.
Решение проблемы 2) в общем случае не известно (1978), но в важном специальном случае, когда Ф состоит из одного дифференциального полинома, полное решение дается двумя теоремами Ритта: теоремой о компонентах и теоремой о низких степенях (см. ниже).
Задача нахождения компонент многообразия {Ф} может быть также редуцирована к проблеме 1) и следующей проблеме: 3) для данных характеристич. множеств Аи Впростых дифференциальных идеалов  и
и 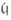 соответственно определить, имеет ли место включение
соответственно определить, имеет ли место включение 
Проблема 3) также далека от решения. В частном елучае, когда Асостоит из одного неприводимого дифференциального полинома Аи q является дифференциальным идеалом [Y1, ..., Yn], это - задача о том, лежит ли точка (0, . . ., 0) в общем решении дифференциального уравнения А = 0.
Проблема 1) решена для конечного множества  "в принципе": при помощи индуктивной процедуры (теория исключения для систем алгебраических дифференциальных уравнений) она сводится к некоторым "более легким" задачам о многочленах от конечного числа неизвестных над
"в принципе": при помощи индуктивной процедуры (теория исключения для систем алгебраических дифференциальных уравнений) она сводится к некоторым "более легким" задачам о многочленах от конечного числа неизвестных над  т. е. задача об алгебраических дифференциальных уравнениях сводится к задаче об алгебраич. уравнениях.
т. е. задача об алгебраических дифференциальных уравнениях сводится к задаче об алгебраич. уравнениях.
Теорема о компонентах утверждает, что особые компоненты являются в свою очередь общими компонентами других дифференциальных полиномов, точнее: пусть 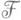 -дифференциальное поле и F-ненулевой дифференциальный полином в
-дифференциальное поле и F-ненулевой дифференциальный полином в 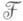 {Y1,..., Yn}. Если р-какая-либо компонента идеала {F} кольца
{Y1,..., Yn}. Если р-какая-либо компонента идеала {F} кольца  {Y1, ...,Yn}, то существует неприводимый дифференциальный полином
{Y1, ...,Yn}, то существует неприводимый дифференциальный полином  такой, что
такой, что  -общая компонента многообразия {В}.
-общая компонента многообразия {В}.
Теорема о низких степенях дает критерий для определения того, является ли общая компонента неприводимого дифференциального полинома 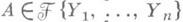 компонентой для {F}. Точнее, пусть
компонентой для {F}. Точнее, пусть  , порядки Fи Аотносительно Yn равны ти lсоответственно, Aj есть j -я производная от Аи S- сепаранта для А. Существуют
, порядки Fи Аотносительно Yn равны ти lсоответственно, Aj есть j -я производная от Аи S- сепаранта для А. Существуют  и r>0 такие, что
и r>0 такие, что

где  никакие два множества i1j, ..., im-l , j не совпадают, порядок cj относительно Yn не превосходит lи cj не делится на А. Если найдено такое разложение, то теорема о низких степенях гласит: общая компонента многообразия {А} является компонентой многообразия {F} тогда и только тогда, когда выписанное разложение содержит член с k А pk, свободный от производных А, и степень к-рого ниже степени любого другого слагаемого в выписанном разложении, рассматриваемом как полином от А, А 1,..., А т_1 (пненулевой характеристике это условие не является ни необходимым, ни достаточным).
никакие два множества i1j, ..., im-l , j не совпадают, порядок cj относительно Yn не превосходит lи cj не делится на А. Если найдено такое разложение, то теорема о низких степенях гласит: общая компонента многообразия {А} является компонентой многообразия {F} тогда и только тогда, когда выписанное разложение содержит член с k А pk, свободный от производных А, и степень к-рого ниже степени любого другого слагаемого в выписанном разложении, рассматриваемом как полином от А, А 1,..., А т_1 (пненулевой характеристике это условие не является ни необходимым, ни достаточным).
Другое направление исследований в Д. а. представляет вопрос о расширении специализаций. Пусть (h1, . .., hn) и (x1, ..., xn) - точки в Un, где U- универсальное расширение дифференциального поля 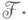 Точка (x1, ..., xn) наз. дифференциальной специализацией точки (h1, ..., hn). над
Точка (x1, ..., xn) наз. дифференциальной специализацией точки (h1, ..., hn). над  (что обозначается, если любой дифференциальный полином
(что обозначается, если любой дифференциальный полином 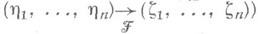 , обращающийся в нуль в (h1, ..., hn), обращается в нуль и в (x1, ..., xn). Если
, обращающийся в нуль в (h1, ..., hn), обращается в нуль и в (x1, ..., xn). Если  и
и  то очевидно, что
то очевидно, что 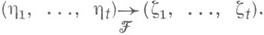 Говорят, что первая специализация является расширением второй.
Говорят, что первая специализация является расширением второй.
Пусть даны (h1, ..., hn) и kи пусть  таков, что
таков, что  Доказано, что существует ненулевой дифференциальный полином В 0
Доказано, что существует ненулевой дифференциальный полином В 0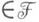 {Y1, ..., Yk}, удовлетворяющий условию
{Y1, ..., Yk}, удовлетворяющий условию  и такой, что любая дифференциальная специализация для которой
и такой, что любая дифференциальная специализация для которой  может
может  быть расширена до дифференциальной специализации
быть расширена до дифференциальной специализации  где
где  Однако, в отличие от ситуации в алгебраич. геометрии, дифференциальная специализация (h1, . . ., hk)
Однако, в отличие от ситуации в алгебраич. геометрии, дифференциальная специализация (h1, . . ., hk) (x1, ..., xk). не всегда может быть расширена до дифференциальной специализации
(x1, ..., xk). не всегда может быть расширена до дифференциальной специализации  даже если элементы xk+1, ..., xn будут принимать значение . Таким образом возникает задача: найти критерий, когда дифференциальная специализация
даже если элементы xk+1, ..., xn будут принимать значение . Таким образом возникает задача: найти критерий, когда дифференциальная специализация  может быть расширена до дифференциальной специализации (h1, ..., hn)
может быть расширена до дифференциальной специализации (h1, ..., hn)
Частный случаи этой проблемы встречается в проблеме неопределенных форм. Пусть полиномы F,  взаимно простые,
взаимно простые,  ' и Fи Gобращаются в нуль в точке (0, . . ., 0). Проблема состоит в том, чтобы отношению F/G приписать значение в точке (0, ..., 0). Пусть элементы
' и Fи Gобращаются в нуль в точке (0, . . ., 0). Проблема состоит в том, чтобы отношению F/G приписать значение в точке (0, ..., 0). Пусть элементы  дифференциально алгебраически независимы над
дифференциально алгебраически независимы над 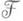 и
и 
Естественно сказать, что F/G допускает значение a. в точке

Таким образом проблема сводится к нахождению расширений 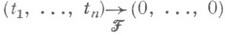 до (t1, ..., tn, и). Это эквивалентно определению элементов
до (t1, ..., tn, и). Это эквивалентно определению элементов  таких, что (0, . . ., 0, а) является нулем общей компоненты дифференциального полинома
таких, что (0, . . ., 0, а) является нулем общей компоненты дифференциального полинома 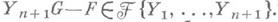
Дж. Ритт (J. Ritt) предположил, что aлибо определено однозначно (возможно, равно бесконечности), либо полностью произвольно; он доказал это предположение для обыкновенных дифференциальных полей при n=1, ord(FG)=1. Изучаются свойства конкретных дифференциальных идеалов в кольце  {Y1, . . ., Yn}. Для бесконечной последовательности S1; . . ., Sp, ... простых дифференциальных идеалов в
{Y1, . . ., Yn}. Для бесконечной последовательности S1; . . ., Sp, ... простых дифференциальных идеалов в  {Y1, ..., Yn}, где каждый Si - собственный делитель идеала Si+1, пересечение всех Si является простым дифференциальным идеалом и размерность соответствующего многообразия
{Y1, ..., Yn}, где каждый Si - собственный делитель идеала Si+1, пересечение всех Si является простым дифференциальным идеалом и размерность соответствующего многообразия 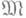 больше размерности многообразия Mi, соответствующего Si для любого i.
больше размерности многообразия Mi, соответствующего Si для любого i.
Из других результатов о дифференциально алгебраич. многообразиях следует отметить аналог теоремы Люрота: если  расширение дифференциального поля
расширение дифференциального поля  к-рое содержится втосодержит
к-рое содержится втосодержит 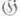 элемент uтакой, что
элемент uтакой, что 

Однако теория дифференциально алгебраич. кривых (многообразий дифференциальной размерности 1) находится в начальной стадии развития; даже для таких инвариантов, как род кривой в алгебраич. геометрии, дифференциально алгебраич. аналоги не найдены. Значительный интерес представляет теория пересечений дифференциально алгебраич. многообразий. Для них неверно утверждение, что пересечение двух неприводимых многообразий размерности ри qв n-мерном аффинном пространстве имеет размерность не менее р+q-n. Однако дифференциально алгебраич. многообразия, кроме размерности, характеризуются также порядком относительно выбранного базиса дифференциальной трансцендентности. Для порядка пересечения многообразий относительно специальным образом выбираемого базиса получены нек-рые оценки сверху. В аналитическом случае доказана следующая теорема о пересечении компонент одного дифференциального полинома: если F- дифференциальный полином от неизвестных Y1, ..., Yn, то нуль полинома F, содержащийся более чем в одной компоненте F, аннулирует дF/дYij для i=1, ..., пи любого j. Понятия дифференциально алгебраич. многообразия можно обобщить (уже не предполагая его аффинным). В частности, можно ввести понятия дифференциально однородных полиномов и проективных дифференциально алгебраич. многообразий.
Для дифференциального поля Fне существует дифференциально алгебраич. замыкания, не существует дифференциально алгебраич. замкнутых полей. Заменой их, в нек-ром смысле, являются так наз. "стесненные" расширения.
Одним из направлений в Д. а. является теория Галуа дифференциальных полей. Для дифференциального поля  строится универсальное дифференциальное расширение Uи рассматривается множество дифференциальных изоморфизмов конечно порожденного дифференциально алгебраич. расширения
строится универсальное дифференциальное расширение Uи рассматривается множество дифференциальных изоморфизмов конечно порожденного дифференциально алгебраич. расширения  поля
поля  в U, тождественных на
в U, тождественных на 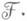 Если
Если  является сильно нормальным расширением
является сильно нормальным расширением 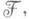 то на множестве G дифференциальных изоморфизмов
то на множестве G дифференциальных изоморфизмов  . в Uможно ввести структуру алгебраич. группы над полем констант К поля U. Частным случаем сильно нормальных расширений являются расширения Пикара - Вессио, получающиеся присоединением к полю
. в Uможно ввести структуру алгебраич. группы над полем констант К поля U. Частным случаем сильно нормальных расширений являются расширения Пикара - Вессио, получающиеся присоединением к полю 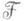 решений линейного однородного дифференциального уравнения с коэффициентами в поле
решений линейного однородного дифференциального уравнения с коэффициентами в поле  Группа Галуа расширения Пикара - Вессио является алгебраической матричной группой. Связь между промежуточными полями и подгруппами группы Gописывается следующей теоремой.
Группа Галуа расширения Пикара - Вессио является алгебраической матричной группой. Связь между промежуточными полями и подгруппами группы Gописывается следующей теоремой.
Пусть 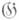 - сильно нормальное расширение дифференциального поля
- сильно нормальное расширение дифференциального поля  с полем констант С. а) Если
с полем констант С. а) Если  - дифференциальное поле такое, что
- дифференциальное поле такое, что  то
то  сильно нормально над
сильно нормально над  , группа Галуа G(
, группа Галуа G( ). является С-подгруппой в
). является С-подгруппой в  и поле инвариантов группы G(
и поле инвариантов группы G(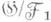 ). в совпадает
). в совпадает 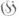 с.
с. б) Если G1 является С-подгруппой группы
б) Если G1 является С-подгруппой группы 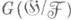 и
и  обозначает множество инвариантов группы G1 в
обозначает множество инвариантов группы G1 в 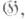 то
то  - дифференциальное поле,
- дифференциальное поле, и
и  =G1.
=G1.
Нормальным делителям G1 группы 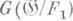 соответствуют при этом сильно нормальные расширения
соответствуют при этом сильно нормальные расширения  поля
поля 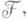 и наоборот. Для связных разрешимых групп решена обратная задача Галуа, т. е. вопрос о существовании у поля
и наоборот. Для связных разрешимых групп решена обратная задача Галуа, т. е. вопрос о существовании у поля  сильно нормального расширения
сильно нормального расширения 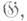 группа Галуа к-рого изоморфна
группа Галуа к-рого изоморфна 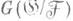 заданной группе. Эта задача сведена к оценке размерности нек-рого векторного пространства над полем констант Споля
заданной группе. Эта задача сведена к оценке размерности нек-рого векторного пространства над полем констант Споля 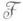 и ранга некоторой абелевой группы. Имеются результаты по теории Галуа бесконечных расширений. Смежными с теорией Галуа вопросами занимается теория интегрирования в конечном виде.
и ранга некоторой абелевой группы. Имеются результаты по теории Галуа бесконечных расширений. Смежными с теорией Галуа вопросами занимается теория интегрирования в конечном виде.
Разрабатывается теория дифференциальных алгебраич. групп, существенно отличающаяся от своего алгебраич. аналога. В частности, дифференциальное кольцо всюду определенных дифференциальных рациональных функций на аффинном дифференциальном алгебраич. множестве не является дифференциальным координатным кольцом, и в общем случае не конечно порождено как дифференциальная алгебра.
Среди результатов о приближении дифференциально алгебраич. функций рациональными может быть отмечен аналог теоремы Лиувилля о приближении алгебраич. чисел рациональными. Однако доказательство аналога теоремы Туэ - Зигеля - Рота остается (1978) проблемой.
Развивается теория колец с высшими дифференцированиями. При изучении объектов ненулевой характеристики высшие дифференцирования представляют более сильное средство. Если характеристика дифференциального кольца Аравна р, то р-я степень любого элемента является константой, в то время как для колец с высшими дифференцированиями это не так. Для колец с высшими дифференцированиями получены аналоги многих перечисленных выше результатов, касающихся как теории пересечения идеалов, так и теории Галуа.
Лит.:[1] Капланский И., Введение в дифференциальную алгебру, пер. с англ., М.. 1959; [2] Ritt J. F.,Difterential algebra, N. Y.,1950; [3]Kolciin E. R., Differential algebra and algebraic groups, N. Y.-L., 1973; [4] его же, Some problems in differential algebra, в сб.: Тр. международного конгресса математиков. Москва 1966, М., 1968.
А. В. Михалев, Е. В. Панкратьев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.