Akademik

интеграл ошибок,- функция

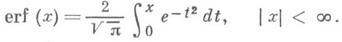
В теории вероятностей используется не И. в., а функция нормального распределения:

- так наз. интеграл вероятности Гаусса. Для случайной величины X, имеющей нормальное распределение с математич. ожиданием 0 и дисперсией s², вероятность неравенства , равна 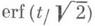. Для действительного хИ. в. принимает действительные значения, в частности

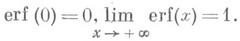
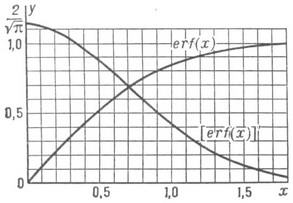
График И. в. и его производной см. на рис. Рассматриваемый и как функция комплексного переменного z, И. в. erf(z) есть целая функция от z.

Асимптотич. представление при больших z, Rez>0:

В окрестности z=0 И. в. представляется в виде ряда

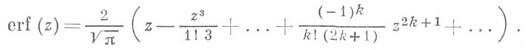
С Френеля интегралами С(z) и S(z)И. в. связан соотношениями:

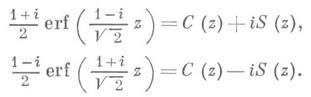
Производная И. в.:

Иногда используются следующие обозначения:

Лит.:[1] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены, пер. с англ., 2 изд., М., 1974; [2] Янке Е., Эмдв Ф., Лёш Ф., Специальные функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М., 1968: [3] Кратцер А., Франц В., Трансцендентные функции, пер. с нем., М., 1963; [4] Лебедев Н. Н., Специальные функции и их приложения, 2 изд., М., 1963.

А. Б. Иванов.