Akademik

- конечное множество точек, прямых, плоскостей, связанных между собой взаимными инцидентностями. К. могут быть как плоскими, так н пространственными.

Плоская конфигурация - конечная система рточек и gпрямых на плоскости, расположенных таким образом, что всякая точка системы инцидентна с одним и тем же числом упрямых этой системы, а всякая прямая инцидентна с одним и том же числом p точек этой системы. Минимальная система точек данной К., из к-рой вся К. может быть получена путем инциденций пар точек с прямыми и пересечений пар прямых, наз. системой образующих данной К. Числа р, g,g, p связаны соотношением pg=gp, a К. обозначается символом (р _g, g_p). К., содержащая одинаковое число точек и прямых, обозначается символом ( р _у).

Примеры плоских К.: 1) Одна точка и одна прямая, инцидентные между собой, образуют К. (1₁). 2) Три точки, не лежащие на одной прямой, и три прямые, инцидентные с каждой парой, образуют К. (3₂),

эта фигура - трехвершинник (или трехсторонник) на плоскости. 3) Полный четырехсторонник - четыре прямые и шесть точек их попарного пересечения образуют К. (6₂, 4₃). Однако здесь не все прямые, соединяющие попарно точки К., являются прямыми этой К.; точки R, P, Q и прямые RP, RQ, PQ не принадлежат ей (рис. 1).

Автоморфизмом К. наз. отображение К. на себя, при к-ром точки К. переходят в точки, прямые - в прямые этой же К., и при этом ни одна инцидентность не пропадает, и не добавляется новых. К. наз. правильной, если группа автоморфизмов этой К. транзитивна.

Для данной К. (р _g, g_p )двойственной наз. К. (g_p, р _g). К. типа (р _g )н только такие, двойственно соответствуют К. такого же типа, они наз. двойственно-инвариантными.

К. наз. проективной, если инцидентность ее элементов сохраняется при проективных преобразованиях. Напр., инцидентность элементов нек-рой К., расположенной на проективной плоскости, обеспечивается выполнением аксиом связи ее, и потому инцидентность точек и прямых К. сохраняется при проективных преобразованиях этой плоскости, а К. будет проективной. Все инцидентности и элементы такой плоской К. могут быть изображены на чертеже с помощью только одной линейки. Плоская К. всегда имеет двойственную вследствие принципа двойственности.

К. может быть определена также как конечная частичная плоскость. Возможность существования нек-рой К. определяется из геометрпч. н комбинаторных соотношений между количеством точек и прямых и количеством взаимных инциденций. К. задается и с помощью абстрактных схем, напр, на таблице (рис. 2) указаны инцидентности (обозначенные крестиком) четырех точек, вершин А _i, и четырех плоскостей, граней D_i тетраэдра. После того как нек-рая К. определена абстрактно, возникает вопрос о ее реализации, т. е. о возможности построения всех инциденций по данной системе образующих. Реализуемость К. как конечной частичной плоскости означает возможность изоморфного отображения ее на нек-рую подплоскость какой-либо плоскости.

К. (р ₂), реализуется в виде р-сторонника так, что вершины и стороны его попарно инцидентны. Абстрактную схему К. (3₂) можно построить, напр., таблицей, как на рис. 2. Плоские К. (р ₃) возможны лишь при так как через каждую точку К. должны проходить три прямые и на каждой из них должны лежать еще две другие точки К. (число р должно удовлетворять неравенству ). К. типа ( р ₃ )допускают модификации, количество к-рых зависит от р. К. (7₃) представляется схемой (рис. 3),

где цифра за фигурной скобкой означает точку пересечения прямых, проходящих через пары точек, записанные слева от скобки, цифры за вертикальной чертой обозначают, те точки, к-рые должны быть коллинеарными при выполнении всех указанных слева инциденций. На действительной проективной плоскости все инцидентности реализуются в полном четырехвершиннике(рис. 4),

однако последняя инциденция (коллинеарность трех точек) здесь не имеет места. К. (9₃) допускает три различные модификации, одна из к-рых (9₃)₁ наз. конфигурацией Брианшона - Паскаля (рис. 5): каждая прямая l_i инцидентна с тремя различными точками а,-, а каждая точка - с тремя различными прямыми.

Эта К. может быть реализована на проективной плоскоcти (рис. 6), она является проективной, правильной, двойственно инвариантной (см. Брианшона теорема, Паскаля теорема).

Две другие модификации К. (9₃)₂, (9₃)₃ (рис 7) существенно отличаются от конфигурации Брианшона -Паскаля. Напр., К. (9₃)₃ не является правильной, а для построения К. (9₃)₂ необходима вспомогательнаякривая 2-го порядка.

К. (10₃) имеет уже десять различных модификаций, из к-рых важнейшей является конфигурация Дезарга (рис. 8).

Она реализуется на действительной проективной плоскости, является проективной, правильной, двойственно инвариантной. Другие девять модификаций . (10₃) не выражают никакой общей геометрич. теоремы, причем лишь восемь из них могут быть реализованы на действительной проективной плоскости, но для их построения требуется специальное расположение системы образующих точек (в частности, К. такого типа реализуются в виде правильных многосторонников (рис. 9).

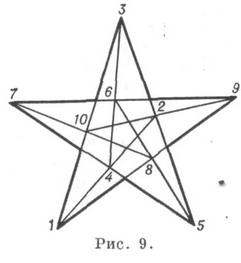
В приведенной на чертеже последовательности вершин также получается вписанный и одновременно описанный десятисторонник. К. (9₃) и (10₃) также допускают геометрич. построение с помощью многосторонников, вписанных и описанных вокруг самих себя, так, К. (9₃)₁ представляется в виде девятисторонника (2, 3, 6, 1, 5, 9, 4, 8, 7, 2) (рис. 6), конфигурация Дезарга - в виде десятисторонника (рис. 8) (1, 2,3,4,5,6, 7, 8,9, 10, 1). Такие представления этих К. единственные точностью до автоморфизмов. Вообще, построение р-сторонников, одновременно вписанных й описанных вокруг самих себя, приводит к К. типа (р ₃). Существуют также представления К. типа ( р ₃ )в виде нескольких многосторонников, вписанных и описанных вокруг друг друга.

Напр., конфигурация Дезарга допускает единственный способ (с точностью до автоморфизма) представления парой взаимно вписанных и описанных пятисторонников (1, 9, 7, 5, 3) и (8, 4, 10, 6, 2) (рис. 8). При увеличении числа рколичество модификаций К. типа ( р ₃). быстро растет.

продолжение Конфигурация...

Пространственная конфигурация - конечная система точек и плоскостей такая, что каждая точка инцидентна с одним и тем же числом плоскостей, а каждая плоскость - с одним и тем же числом точек. Наряду с К., состоящей из точек и плоскостей, в пространстве рассматриваются и К., состоящие из точек и прямых. Так, рассмотренная выше конфигурация Дезарга, состоящая из точек и прямых, предедавляет собой также и пространственную К. (10₃) (рис. 8), если соответствующие трехсторонники лежат в различных плоскостях; одновременно ее можно рассматривать как К. (10₃, 5₆), составленную из точек и плоскостей: шесть вершин соответствующих трехсторонников, центр перспективы и три точки на оси перспективы, в к-рых сходятся соответствующие стороны трехсторонников, дают всего десять точек, а три плоскости, образованные соответствующими сторонами трехсторонников, и две плоскости самих трехсторонников дают всего пять плоскостей. В каждой плоскости шесть точек К., и каждая точка инцидентна трем различным плоскостям.

Тривиальной пространственной К. типа (р _g). является К. (4₃), ее схема - на рис. 2; она изображается тетраэдром. К. типа (р ₄) для невозможна, при р=8 имеется пять различных схем К., одна из к-рых, так наз. конфигурация Мёбиуса, состоит из двух тетраэдров, вписанных и описанных друг около друга. Каждой из восьми точек - вершин тетраэдров - инцидентны четыре плоскости граней тетраэдров, а каждой из восьми плоскостей инцидентны четыре точки - вершины. При переходе к К. более высокого порядка число возможных модификаций быстро возрастает, напр., К. (9₄) имеет уже 26 геометрич. осуществимых модификаций.

Из пространственных К. более высокого порядка примечательны конфигурация Рейе и конфигурация Шлефли. Конфигурацией Рейе наз. состоящая из точек и плоскостей К. (12₆). В действительном проективном пространстве ее можно построить, напр., из вершин нек-рого куба, его центра, трех (бесконечно удаленных) точек, в к-рых сходятся параллельные ребра куба, а плоскостями этой К. являются шесть граней куба и шесть его диагональных плоскостей, проходящих через пары противоположных ребер (рис. 10).

Конфигурация Рейе является проективной, правильной и двойственно инвариантной, причем изображение этой К. можно построить (согласно большому принципу двойственности), используя вместо куба октаэдр (рис. 11).

Конфигурацию Рейе можно рассматривать также как пространственную К. точек и прямых (12₄, 16₃). К. (30₂, 12₅), состоящая из точек и прямых, наз. двойным шестисторонником Шлефли. Он изображается в пространстве, напр., в виде симметрично расположенных прямых и точек на каждой грани куба (по одной из двух шестерок) (рис. 12).

Не всякая плоская К. может быть реализована на действительной проективной плоскости. Напр., К. (7₃) и (8₃) не реализуются на ней, в связи с чем возникает задача реализации К. на каких-либо других проективных плоскостях. Каждое предложение, утверждающее, что из реализуемости в данной плоскости нек-рой К. со всеми инцидентностями, кроме, быть может, одной, вытекает реализуемость К. со всеми ее инци-дентностями, называется конфигурационным предложением данной плоскости. Таким образом, если все инцидентности некоторой К. реализуются на данной плоскости вследствие геометрических свойств этой плоскости, то К. реализуется на этой плоскости. Например, К. (9₃)₁. всегда реализуется на действительной проективной плоскости, так как из реализуемости всех инциденцпй, кроме одной, последняя инцидентность выполняется всегда вследствие теорем Брианшона и Паскаля, т. е. эти теоремы являются конфигурационными предложениями. Выполнение последней инцидентности в К. (7₃) (рис. 4) на такой плоскости не имеет места (так как диагональные точки полного четырехвершинника не принадлежат одной прямой), поэтому такое утверждение не является конфигурационным предложением. Однако оно будет таковым в комплексной проективной плоскости. Подобным образом рассматривается и реализуемость других К.; в частности, К. (8₃) может быть реализована в конечных папповых плоскостях, построенных над полями Галуа с тремя и четырьмя элементами.

Конфигурационные предложения, справедливые в данной плоскости, определенным образом организуют элементы этой плоскости и потому играют роль при аксиоматическом построении геометрии этой плоскости. Напр., если в данной плоскости выполняются все аксиомы связи проективной плоскости, но но реализуется конфигурация Дезарга, то данная плоскость несет на себе так наз. недезаргову геометрию. Конфигурационное предложение может быть также записано в алгебраич. форме в виде нек-рого алгебраич. тождества. В произвольной проективной плоскости конфигурационные предложения могут вводиться лишь в качестве новых аксиом, причем постулирование одного какого-нибудь конфигурационного предложения может повлечь за собой справедливость других конфигурационных предложений в этой плоскости. Вообще говоря, всякому алгебраич. тождеству соответствует конфигурационное предложение, к-рое наз. геометрич. представлением этого тождества в определенной плоскости, где реализуется К. (однако не установлено, всякое ли конфигурационное предложение является геометрич. представлением определенного вида тождества в алгебре тернаров и натуральных тел проективной плоскости). Исследование подобных алгебраич. эквивалентов позволяет изучать как свойства К., так и возможность их реализуемости как конечной частичной плоскости в определенной проективной плоскости, а также логическую связь между различными конфигурационными предложениями.

Теория К. находит применение в решении ряда геометрич. вопросов. Так, плоская К. (8₃) играет важную роль в теории плоских кривых третьего порядка, не имеющих двойных точек, в частности, при исследовании их точек перегиба. Конфигурация Рейе применяется при изучении правильных многогранников в четырехмерном евклидовом пространстве Е ⁴. Правильный многогранник в Е ⁴ ограничен областями, являющимися правильными трехмерными многогранниками. Правильный многогранник в Е ⁴ наз. n-ячейкой, если он ограничен пправильными многогранниками. Напр., 5-ячейка ограничена пятью трехмерными тетраэдрами, 8-ячейка - восемью кубами и т. д., причем 5-ячейка и 24-ячейка являются двойственными сами себе (точки соответствуют пространствам, а прямые - плоскостям). Изучение правильных ячеек проводится исследованием их проекций в Е ³. Если в качестве пространства проекции выбирается для 24-ячейки нек-рая трехмернаягрань, то получается разделение пространства на 12-октаэдров, из к-рых все, не считая среднего, простираются в бесконечность, что приводит к такому виду проекции, к-рая составляет конфигурацию Рейе (рис. 10). Если в качестве пространства проекции берется трехмерное пространство, проходящее через вершину 24-ячейки, то получается также конфигурация Peйe (рис. 11). (Проекция 24-ячейки в трехмерное пространство - на рис. 13.)

Конфигурация Рейе возникает и в системе точек и осей подобия четырех шаров, центры к-рых не лежат все в одной плоскости. В этой системе каждая ось инцидентна с тремя точками, и каждая точка - с четырьмя осями, получается пространственная К. (12₄, 16₃) точек и прямых. Каждые три точки - центры подобия - определяют по одной плоскости, каждые две оси, инцидентные с точкой подобия, образуют еще восемь различных плоскостей, всего 12, каждая из к-рых инцидентна с шестью точками подобия, а каждая из двенадцати точек подобия - с шестью плоскостями, т. е. получается К. (12₆). К., представляемая двойным шестисторойником Шлефли, применяется для изучения свойств алгебраич. поверхностей третьего порядка, к-рая определяется 19 точками и всегда проходит через нек-рый двойной шестисторонник Шлефли. При этом существенным является то, что любые четыре прямые его имеют гиперболоидальное расположение.

Конфигурационные предложения о реализации инцидентностей на плоскости применяются для изучения свойств многосторойников (многовершинников) и для решения задач на построение при различных ограничениях (построение с недоступными элементами, построение одной линейкой и т. д.). В кинематике и графической статике находит практическое применение теория К. полиэдров.

Возможны К., составленные из других геометрич. элементов, напр, из кругов произвольной размерности и единичного радиуса в Е ^п.

Лит.:[1] Гильберт Д., Кой-Фоссен С, Наглядная геометрия, пер. с нем., 2 изд., М.-Л., 1951; [2] Скорняков Л. А., "Успехи матем. наук", 1951, т. 6, в. 6, с. 112- 154; [3] Аргунов Б. И., "Матем. сб.", 1950, т. 26, № 3, с. 425-56; [4] Levi F., Geometrische Konfigurationenen, Lpz., 1929.

Л. А. Сидоров.