Akademik

- форма от (n+1)(N+1).переменных, где n=dim X, а X - замкнутое алгебраическое подмногообразие N-мерного проективного пространства однозначно с точностью до умножения на константу определяемая по Xи сама однозначно определяющая X. Точное определение К. ф. состоит в следующем. Пусть есть N-мерное проективное пространство всех гиперплоскостей в 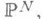Г - подмножество в многообразии

состоящее из всех таких наборов что точка лежит в пересечении гиперплоскостей и

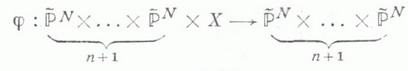
- естественная проекция. Тогда j(Г)есть неприводимое подмногообразие коразмерности 1 в

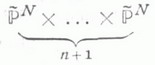
и потому j(Г) является многообразием нулей нек-рой формы F_X на

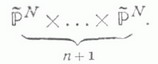
Всегда можно считать, что F_X не имеет кратных: множителей, и это условие определяет F_X по X однозначно с точностью до умножения на константу. Наоборот, FX однозначно определяет множество всевозможных наборов n+1 гиперплоскостей в пересекающихся по точкам из X, и потому F_X однозначно определяет X. Форма F_X и наз. формой Кэли многообразия X.

Часто К. ф. наз. также ф о р м о й Ч ж о у, или ассоциированной формой многообразия X. Идея определения Xкомплексом линейных подпространств размерности N-п-1 в 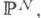пересекающих X, восходит к А. Кэли [5], к-рый применил ее для случая n=1, N=3. Коэффициенты К. ф. наз. координатами Чжоу многообразия X.

К. ф. FX однородна по каждой из n+1 систем координат пространства

(1-я система координат - это система координат i-ro сомножителя указанного пространства). Степени однородности F_X по каждой из систем координат совпадают. Эта общая степень dобозначается через deg X, наз. степенью подмногообразия X, и имеет следующий геометрич. смысл: dесть максимум числа точек пересечения Xсовсевозможными (N-n)-мерными линейными пространствами Lв 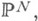для к-рых 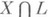- конечное множество (т. е. d - это число точек пересечения Xс "общим" (N-n)-мериым линейным подпространством).

Множество всех форм (рассматриваемых с точностью до умножения на ненулевую константу) от n+1 групп переменных по N+1 переменных, имеющих степень dпо каждой группе, образует проективное пространство 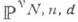нек-рой размерности 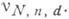К. ф. F_X можно отождествить с точкой 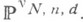Множество 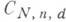всех точек в 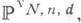являющихся К. ф. n-мерныхзамкнутых подмногообразий степени dв есть квазипроективное многообразие; оно параметризует семейство всех таких подмногообразий, причем указанное семейство является алгебраическим относительно этой параметризации. В общем случае не замкнуто в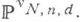

Конструкция К. ф. естественно распространяется на замкнутые n-мерные циклы в 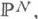т. е. формальные линейные комбинации замкнутых n-мерных подмногообразий 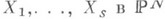с целыми коэффициентами m_i> 0. А именно, полагают

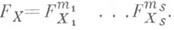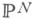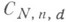и Множество всех К. ф. n-мерных циклов степени dв замкнуто в Изучение К. ф. и свойств многообразий и 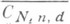является важным моментом в проблеме классификации подмногообразий и циклов в 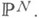Первый шаг в этой классификации состоит в изучении разбиения на неприводимые компоненты. Напр., для N=3, п=1, d=2 (кривые степени 2 в трехмерном пространстве) многообразие состоит из двух неприводимых компонент размерности 8. Первая компонента соответствует плоским кривым второго порядка, а вторая - парам прямых. Бирациональная классификация многообразий является важной проблемой (во всех известных примерах такие многообразия рациональны).

Лит.:[1] Ш а ф а р е в и ч И. Р., Основы алгебраической геометрии, М., 1972; [2] X о д ж В., П и д о Д., Методы алгебраической геометрии, пер. с англ., т. 2, М., 1954; [3] Samuеl P., Methodcs d'algebre abstraite en geometrie algebrique, 2 ed., В., 1967; [4] Chow W.- L., van der Waerden B. L., "Math. Ann.", 1937, Bd 113, S. 692-704; [5] С а у l е у A., Collected mathematical papers, v. 4, Cambr., 1891, p. 446-55. В. Л. Попов.