Akademik

прямоугольная матрица размера каждая строка к-рой является перестановкой (без повторений) элементов множества S, состоящего из га элементов, причем в столбцах каждый элемент встречается не более одного раза. При m = n Л. п. является латинским квадратом порядка п. Обычно S= {1, 2,. . ., п}, и о Л. п. говорят, что он построен на множестве S.

Л. п. существует при любых натуральных т, п, Примером Л. п. может служить матрица, первая строка к-рой есть (1, 2, . . ., га), а все последующие получаются из предыдущей циклич. сдвигом на один шаг. Л. п. размера всегда может быть дополнен до латинского квадрата порядка птак, что первые m строк латинского квадрата будут совпадать со строками Л. п.

Для числа L (m, n) Л. п. размера верна следующая оценка снизу:

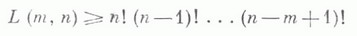
Л. п. наз. нормализованным, если его первая строка есть (1, 2,. . ., п). Число К( т, п).нормализованных Л. п. связано с L(m, п).соотношением:

Подсчет L(m, п).при m = 2,3 связан с классич. комбинаторными задачами:с задачей о числе беспорядков (см. Инверсия).и с задачей о супружеских парах. Так, число беспорядков D_n=K(2, п), а число размещений U_n в задаче о супружеских парах есть число Л. п. размера первые две строки к-рых суть:

Для U_n верны формулы:

Число К(3, п).выражается через D_k и U_i:

где Верна также следующая асимптотика:

где - Эрмита многочлен. Известно также, что

Задача о перечислении Л. п., имеющих более трех строк, не решена (1982). При так, что получена асимптотика:

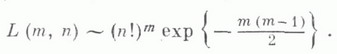
На Л. п. распространяются нек-рые понятия и теоремы, связанные с латинскими квадратами. Так, два Л. п. размера 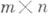наз. ортогональными, если все пары вида различны. Множество Л. п., в к-ром любые два Л. п. ортогональны, имеет не более т-1 Л. п.

Часто под Л. п. понимают следующее обобщение Л. п.: латинским прямоугольником размера построенным на множестве 5, состоящем из пэлементов, наз. матрица размера с элементами из S, встречающимися в каждой строке и каждом столбце не более одного раза. Л. п. размера построенный на псимволах, может быть расширен до латинского квадрата порядка птогда и только тогда, когда каждый символ встречается в Л. п. не менее r+s-п раз.

Лит.:[1] Риордан Д ж., Введение в комбинаторный анализ, пер. с англ., М., 1963. См. также лит. при ст. Латинский квадрат. В. М. Михеев.