Akademik

комбинаторная математика, комбинаторика,- раздел математики, посвященный решению задач выбора и расположения элементов нек-рого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения нек-рой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией. Поэтому можно сказать, что целью К. а. является изучение комбинаторных конфигураций. Это изучение включает в себя вопросы существования комбинаторных конфигураций, алгоритмы их построения, оптимизацию таких алгоритмов, а также решение задач перечисления, в частности определение числа конфигураций данного класса. Простейшими примерами комбинаторных конфигураций являются перестановки, сочетания и размещения.

Множество Xиз пэлементов наз. n-м ножеством; любое его m-подмножество,наз. сочетанием объема т. Число сочетаний объема тиз празличных элементов равно

Имеет место формула:

обычно называемая формулой бинома Ньютона. Числа наз. биномиальными коэффициентами. Упорядоченное m-подмножество наз. размещением объема т. Число размещений объема тиз празличных элементов равно

При т= п размещение представляет собой перестановку элементов множества X, причем число таких перестановок равно Р(п) = п!

Возникновение основных понятий и развитие К. а. шло параллельно с развитием других разделов математики, таких, как алгебра, теория чисел, теория вероятностей, с к-рыми К. а. тесно связан. Еще математикам Древнего Востока были известны формула, выражающая число сочетаний через биномиальные коэффициенты, и формула бинома Ньютона с натуральным показателем п. С мистическими целями изучались магические квадраты3-го порядка. Рождение К. а. как раздела математики связано с трудами Б. Паскаля (В. Pascal) и П. Ферма (P. Fermat) по теории азартных игр. Этн труды, составившие основу теории вероятностей, одновременно содержали принципы определения числа комбинаций элементов конечного множества, устанавливая тем самым ставшую затем традиционной связь К. а. с теорией вероятностей.

Большой вклад в систематическое развитие комбинаторных методов был сделан Г. Лейбницем (G. Leibniz) в его диссертации "Ars Combinatoria" ("Комбинаторное искусство"), где, по-видимому, впервые появился термин "комбинаторный". Большое значение для становления К. а. имела работа Я. Бернулли (J. Bernoulli) "Ars conjectandi" ("Искусство предположений"), посвященная основным понятиям теории вероятностей, где обстоятельно изложен ряд комбинаторных понятий и указаны их применения для вычисления вероятностей. Можно считать, что с появлением работ Г. Лейбница и Я. Бернулли комбинаторные методы выделились в самостоятельную часть математики.

Большой вклад в развитие комбинаторных методов сделал Л. Эйлер (L. Euler). В его работах по разбиениям и композициям натуральных чисел на слагаемые было положено начало одному из основных методов перечисления комбинаторных конфигураций - методу производящих функций.

Возрождение интереса к К. а. относится к 50-м гг. 20 в. в связи с бурным развитием кибернетики и дискретной математики и широким использованием электронно-вычислительной техники. В этот период активизировался интерес к классическим комбинаторным задачам.

На формирование направлений исследований в дальнейшем оказывают влияние два фактора. С одной стороны, выбор объектов исследований, с другой стороны - формулировка целей исследования, зависящая в конечном счете от сложности изучаемых объектов. Если исследуемая комбинаторная конфигурация имеет сложный характер, то целью исследования является выяснение условий ее существования и разработка алгоритмов построения.

Большой развивающийся раздел К. а. составляет теория блок-схем (см. также [2], [3], [10]); основные проблемы этого раздела связаны с вопросами классификации, условиями существования и методами построения нек-рых классов блок-схем. Частным случаем блок-схем являются так наз. уравновешенные неполные блок-схемы, или (b, v, r, k,l)-конфигурации, к-рые определяются как совокупности из bk-подмножеств нек-рого v-множества, называемых блоками, с условием, что каждый элемент появляется в r блоках, а каждая пара элементов - в l блоках. При b=vи, следовательно, r=k(b, v, r, k,l)-конфигурацня наз. (v, k,l)-конфигурацией, или симметричной уравновешенной неполной блок-схемой. Даже для (v, k,l)-конфигураций вопрос о необходимых и достаточных условиях их существования остается пока (1978) открытым. Для существования (v, k,l)-конфигураций необходимо, чтобы при vчетном k-l было квадратом, а при vнечетном уравнение

имело решение в целых числах х, у, z, одновременно не равных нулю.

При v=n²+n+1, k=n+1, l=1 (v, k,l)-конфигурация представляет собой проективную плоскость порядка и, являющуюся частным случаем конечной геометрии, содержащей конечное число точек и прямых с заданными условиями их инцидентности. Каждой проективной плоскости порядка п-1 можно поставить во взаимно однозначное соответствие полное множество из п-1 попарно ортогональных латинских квадратов порядка п. Для существования проективной плоскости порядка и необходимо, чтобы при n=1, 2 (mod 4) существовали целые числа аи b, удовлетворяющие равенству n=а ²+b².

Вопрос о существовании проективных плоскостей порядка прешен положительно только для п=р^a, где р- простое, а a - натуральное числа. Даже для n=10 этот вопрос является открытым (1978). К этому кругу вопросов относится результат, связанный с опровержением гипотезы Эйлера о несуществовании пары ортогональных латинских квадратов порядка n=4k+2, k=1, 2, ... (см. Комбинаторные задачи).

Другое направление К. а. связано с выбора теоремами. В основе целого ряда результатов этого направления лежит теорема Ф. Холла о существовании системы различных представителей (трансверсали) семейства подмножеств (Х ₁, ..., Х _n )множества X, т. е. системы элементов ( х ₁,..., х _п )такой, что х _i О Х и х _i неравно х _j при i неравно j:трансверсаль существует тогда и только тогда, когда для любых i₁, ... , i_k таких, что справедливо неравенство 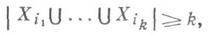где |Y|- число элементов в множестве Y. Из теоремы Ф. Холла вытекает теорема о существовании латинского квадрата, состоящая в том, что любой латинский прямоугольник размера 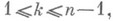можно дополнить до латинского квадрата порядка п. Другое следствие теоремы Ф. Холла: любую неотрицательную матрицу А= ||a_ij||, i, j=1, ..., п, такую, что

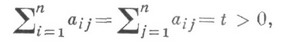
можно представить в виде

где П ₁, ..., П _s - матрицы подстановки порядка пи Из теоремы Ф. Холла следует также теорема о том, что минимальное число строк и столбцов неотрицательной матрицы, содержащих все положительные элементы, равно максимальному числу элементов, попарно не расположенных в одной и той же строке или в одном и том же столбце. Экстремальное свойство частично упорядоченных множеств, аналогичное этой теореме, устанавливает теорема, утверждающая, что минимальное число непересекающихся цепей совпадает с объемом максимального подмножества, состоящего из попарно несравнимых элементов. Экстремальный характер носит и следующая теорема: если для n-множества X составить все (ⁿ_r )сочетаний по r элементов и разбить их на кнепересекающихся классов, то для целого тсуществует число п ₀=п ₀( т, r, k )такое, что при найдется подмножество из тэлементов для к-рого все (^m_r )сочетаний принадлежат одному классу.

Экстремальной является задача коммивояжера, заключающаяся в составлении кратчайшего маршрута посещения пгородов с возвращением в исходный пункт при условии, что расстояния между городами известны. Эта задача имеет приложения к изучению транспортных сетей. Комбинаторные задачи экстремального характера рассматриваются в теории потоков в сетях и в теории графов.

Значительную часть К. а. составляют перечислительные задачи. При их решении либо указывается метод перебора комбинаторных конфигураций из данного класса, либо определяется их число, либо делается то и другое. Типичные результаты перечислительных задач: число подстановок степени пc k циклами равно |S(n, к)|, где S(n, к)- числа Стирлинга 1-го рода, определяемые равенством

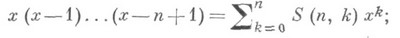
число разбиений множества из пэлементов на кподмножеств равно числу Стирлинга 2-го рода

число размещений тразличных предметов в празличных ячейках, когда пустых ячеек нет, равно п!s( т, п). Полезным инструментом для решений перечислительных задач является пер. манент матрицы. Перманент матрицы А =||а _ij||,i=1, ..., п, j=1, ..., т,с элементами из нек-рого кольца определяется равенством

где суммирование производится по всевозможным размещениям объема пиз тразличных элементов.

Число трансверсалей нек-рого семейства подмножеств конечного множества равно перманенту соответствующей матрицы инцидентности.

К вычислению перманентов сводится целый класс задач по определению числа перестановок с ограниченными позициями. Эти задачи для удобства иногда формулируются как задачи о расстановке взаимно неатакующих фигур на шахматной доске размером С определением перманентов нек-рых классов матриц связаны варианты задачи о димерах, возникающей при изучении явления адсорбции и заключающейся в определении числа способов объединения атомов в двухатомные молекулы на нек-рой поверхности. Ее решение может быть также получено через пфаффианы - некоторые функции от матриц, близкие к определителям. Проблема о числе латинских прямоугольников (квадратов) также связана с разработкой эффективных методов вычисления перманентов нек-рых (0, 1)-матриц.

Для вычисления перманентов применяется формула:

Имеется большое число неравенств, дающих оценку величины перманента в нек-рых классах матриц. Представляет интерес определение экстремальных значений перманента в определенных классах неотрицательных матриц, однако эта задача не решена (1978) даже для (О, 1)-матриц с заданным значением числа единиц в строках и столбцах. К этой проблеме примыкает гипотеза Ван дер Вардена о том, что минимум перманента дважды стохастической матрицы порядка правен n!/nⁿ, подтвержденная только для положительно полуопределенных матриц.

Большую роль в решении перечислительных задач играет метод производящих функций. Производящая функция ставится в соответствие последовательности (а ₀, a₁,...) с элементами из нек-рого поля и рассматривается как формальный степенной ряд. При таком определении производящие функции эффективно используются для решения перечислительных задач параллельно с методами рекуррентных соотношений и конечно разностных уравнений. При получении асимптотических формул в качестве производящих функций обычно используются аналитические функции действительного или комплексного переменного. В последнем случае для отыскания выражений коэффициентов применяют интегральную формулу Коши.

Имеются результаты в направлении возможной унификации методов перечисления, связанные с рассмотрением так наз. алгебр инцидентности и использованием функции Мёбиуса на частично упорядоченных множествах (см., напр., [10]). При решении перечислительных задач существенную роль играет формализация понятия неразличимости объектов. Использование для этих целей понятия эквивалентности объектов относительно нек-рой группы подстановок в сочетании с применением метода производящих функций было положено в основу так наз. теории перечисления Пойа (см. [10]). Сущность этой теории состоит в следующем. Рассматривается Y^x - множество конфигураций

f:X ->Y,| Х| = т, |Y|= n.

На множестве Xдействует группа подстановок А, определяющая на Y^X отношение эквивалентности , при к-ром 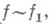если существует такое что f(a(x))=f₁(x). для всех Каждому 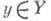ставится в соответствие характеристика [y] = (х ₁, . . ., х _k), где s_i, i=l, ..., k,- элементы абелевой группы. Характеристика конфигурации f задается равенством

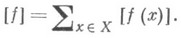
Если a(s₁,..., s_k) - число элементов с заданным значением характеристики и b_m(s₁,..., s_k) - число неэквивалентных конфигураций

то основная теорема Пойа утверждает, что

где Zесть циклический индекс группы А, определяемый равенством

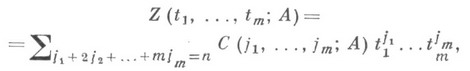
C(j₁, ..., j_m; А )-число элементов циклового класса {1^j12^j2 ...т ^j т} группы А. Эта теорема основана на лемме Бернсайда: число классов эквивалентности N(А), определяемых на множестве Xгруппой подстановок А, дается формулой

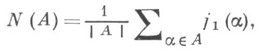
где j₁(a) - число единичных циклов Теория Пойа имеет применения при решении перечислительных задач теории графов и перечислении углеродных химических соединений. Имеется обобщение теории Пойа на случай, когда эквивалентность конфигураций определяется двумя группами Gи Н, действующими на Xи Yсоответственно (см. [4] и [10]). В таком виде она применяется, напр., для определения числа неизоморфных абстрактных автоматов.

Если X={1, ..., т}, Y={a₁, . .., а _п} и а: где а,- используется а _j раз в качестве образа, то выражение

наз. первичной спецификацией а. Если числа a₁, a₂, ..., a_n содержат b₀ нулей, b₁ единиц и т. д., то выражение

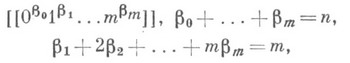
наз. вторичной спецификацией. При нек-рой специализации групп Gи Н, определяющих эквивалентность конфигураций можно указать способ построения производящих функций для перечисления неэквивалентных конфигураций. Этот способ, называемый общей комбинаторной схемой, подразделяется на четыре частных случая в соответствии с тем, принимают группы G и H значения единичной Еили симметрической S_n групп соответствующих степеней. Эти частные случаи являются моделями для большинства известных комбинаторных схем (см. [9], [10]).

1. Коммутативный несимметричней случай: G=S_m, H=E. Моделирует схемы сочетаний, заполнений одинаковых предметов в различные ячейки п др. Производящая функция для перечисления неэквивалентных конфигураций а таких, что

имеет вид:

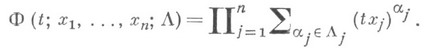
2. Некоммутативный несимметричный случай: G=E, Н-Е. Моделирует схемы размещений, заполнений различимых предметов в различные ячейки и др. Производящая функция для перечисления неэквивалентных конфигураций sтаких, что

имеет вид:

3. Коммутативный симметричный случай: G=5_m, H=S_n. Моделирует схемы заполнения одинаковых предметов в одинаковые ячейки, перечисления разбиений натуральных чисел и др. Перечисление конфигураций а таких, что

основано на использовании производящей функции вида:

4. Некоммутативный симметричный случай: G=E, H=S_n. Моделирует схемы разбиений конечных множеств на блоки, заполнения различимых предметов в одинаковые ячейки и др. Перечисление конфигураций а таких, что

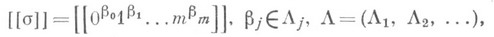
основано на использовании производящей функции вида:

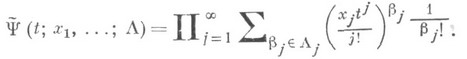
Значительное место в К. а. занимают асимптотические методы. Они применяются как для упрощения сложных конечных выражений при больших значениях входящих в них параметров, так и при получении приближенных формул обходными путями, когда точные формулы неизвестны. Комбинаторную задачу перечислительного характера иногда удобно сформулировать как задачу отыскания характеристик распределения нек-рой случайной величины. Такая интерпретация дает возможность применять развитый аппарат теории вероятностей, а для отыскания асимптотик - предельные теоремы. Детальному исследованию с этих позиций подвергнута классическая схема случайных размещений предметов в ячейки, случайные разбиения множеств, цикловая структура случайных подстановок, а также различные классы случайных графов, включая графы отображений (см. [8], [9]).

Вероятностный подход применяется при изучении комбинаторных свойств симметрических групп и полугрупп. Исследовано предельное распределение порядка случайного элемента симметрической группы S_n при а также асимптотика вероятности порождения ее случайными элементами. Для нек-рых классов случайных неотрицательных матриц изучались распределения числа нулевых линий в матрице и перманентов, даны оценки вероятности примитивности таких матриц. Для доказательства существования комбинаторных конфигураций без их конструирования иногда используется нек-рый специфический вероятностный прием. Сущность этого приема заключается в установлении существования конфигурации без ее конструирования с помощью оценки вероятности нек-рого события (см. [7]).

Лит.:[1] Риордан Дж.. Введение в комбинаторный анализ, пер. с англ., М., 1963; [2] Райзер Г.-Д ж., Комбинаторная математика, пер. с англ., М., 1966; [3] Холл М., Комбинаторика, пер. с англ., М., 1970; [4] Прикладная комбинаторная математика, сб. статей, пер. с англ., М., 1968; [5] Xарари Ф., Теория графов, пер. с англ., М., 1973; [6] Харари Ф., Иалмер Э., Перечисление графов, пер. с англ., М., 1977; [7] Эрдёш П., Спенсер Дж., Вероятностные методы в комбинаторике, пер. с англ., М., 1976; [8] Колчин В. Ф., Чистяков В. П., в кн.: Итоги науки и техники. Теория вероятностей. Математическая статистика. Теоретическая кибернетика, т. 11, М., 1974, с. 5-45; [9] Сачков В. Н., в кн.: Вопросы кибернетики. Тр. семинара по комбинаторной математике, М., 1973, с. 146-64; [10] его же, Комбинаторные методы дискретной математики, М., 1977.

В. Н. Сачков.