Akademik

группа Ли, пильпотентная как абстрактная группа. Абелева группа Ли нильпотентна. Если - флаг в конечномерном векторном пространстве Vнад полем К, то

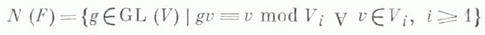
будет нильпотентной алгебраич. группой над А; в базисе, согласованном с флагом F, ее элементы представляются верхними треугольными матрицами с единицами на главной диагонали. Если F - полный флаг (т. е. dim V_k = k), то соответствующая N(F).матричная Ли н. г. N( п, k).состоит из всех матриц порядка n=dim Vуказанного выше вида.

Если К - полное нормированное поле, то N(F) - Ли н. г. над К. Ее алгеброй Ли служит 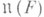(см. Ли нильпотентная алгебра). Вообще, алгебра Ли группы Ли G над полем Кхарактеристики 0 нильпотентна тогда и только тогда, когда нильпотентна связная компонента единицы G₀ группы G. Это позволяет перенести на Ли н. г. свойства нильпотентных алгебр Ли (см. [2], [4], [5]). Групповой вариант теоремы Энгеля при этом допускает следующее усиление (теорема К о л ч и н а): если G - подгруппа в GL(V), где V - конечномерное векторное пространство над произвольным полем К, а каждый 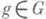унипотентен, то существует такой полный флаг Fв F, что 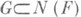(при этом Gавтоматически оказывается нильпотентной) (см. [3]).

Ли н. г., разрешимы, поэтому свойства Ли разрешимых групп переносятся и на них, причем часто в усиленной форме, ибо всякая Ли н. г. треугольна. Связная группа Ли G нильпотентна тогда и только тогда, когда в канонич. координатах ( см. Ли группа).групповая операция в Gзаписывается полиномиально [4]. Всякая односвязная вещественная Ли н. г. Gизоморфна алгебраич. группе, более того - алгебраич. подгруппе в При этом точное представление группы G в 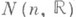можно выбрать так, чтобы группа автоморфизмов Aut G вкладывалась в 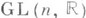- нормализатор образа группы G [см. [1]).

Если G - связная матричная вещественная Ли н. г., то она разлагается в прямое произведение компактной абелевой и односвязной групп Ли. Связная линейная алгебраич. группа G над полем характеристики 0 разлагается в прямое произведение абелева нормального делителя, состоящего из полупростых элементов, и нормального делителя, состоящего из унипотентных элементов [5].

Ранее Ли н. г. наз. специальными группами Ли, или группами Ли ранга 0. В теории представлений полупростых групп Ли при изучении дискретных подгрупп в таких группах существенно используются орисферич. группы Ли, являющиеся Ли н. г.

Лит.:[1] Birkhoff G., "Ann. Math.", 1937, v. 38, p. 526-32; [2] Б у р б а к и Н., Группы и алгебры Ли. Алгебры Ли, свободные алгебры Ли и группы Ли, пер. с франц., М., 1976; [3] С е р р Ж.-П., Алгебры Ли и группы Ли, пер. с англ. и франц., М., 1969; [4] Хелгасон С., Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964; [5] Ш е в а л л е К., Теория групп Ли, пер. с франц., т. 3, М., 1958. В. В. Горбацееич.