Akademik

кривая,- геометрическое понятие, точное и в то же время достаточно общее определение к-рого представляет значитю трудности и осуществляется в разных разделах геометрии различно.

В рамках элементарной геометрии понятие Л. не получает отчетливой формулировки и иногда определяется как "длина без ширины" или как "граница поверхности". По существу в элементарной геометрии изучение Л. сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных Л. (конич. сечения, нек-рые алгебраич. Л. высших порядков и трансцендентные Л.), применяя в каждом случае специальные приемы.

В аналитич. еометрии Л. на плоскости определяется как множество точек, координаты к-рых удовлетворяют уравнению F(x, у)=0. При этом на функцию Fдолжны быть наложены ограничения так, чтобы, с одной стороны, уравнение это имело бесконечное множество решений и, с другой стороны, чтобы это множество решений не заполняло "куска плоскости".

Важный класс Л. составляют те, для к-рых функция F(x, у).есть многочлен от двух переменных; в этом случае Л., определяемая уравнением F(x, y) = 0, наз. алгебраической. Алгебраич. Л., задаваемые уравнением 1-й степени, суть прямые. Уравнение 2-й степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или Л., распадающуюся на две прямые. Алгебраич. Л., определяемые уравнениями высших степеней, рассматриваются в алгебраич. геометрии. При этом большую стройность приобретает их теория, если рассмотрение ведется на комплексной проективной плоскости. В этом случае алгебранч. Л. определяется уравнением вида

где F - однородный многочлен трех переменных, являющихся проективными координатами точек.

Для тех разделов математики, в к-рых господствуют методы теории функций (анализ, дифференциальная геометрия и др.), естественное определение Л.- задание ее пара метрически мп уравнениями. Так, в случае плоскости, Л., заданная параметрич. уравнениями

где - непрерывные функции, определенные на отрезке 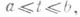есть множество точек ( х, у), соответствующих всевозможным значениям параметра tпри условии, что эти точки рассматриваются в определенном порядке: если точка M₁ соответствует значению параметра t₁ а точка М ₂ - значению t₂, то М ₁ считается предшествующей М ₂ при t₁<t₂;точки, отвечающие различным значениям параметра, считаются различными. Уравнения задают ту же Л., что и уравнения (1), если существует такой гомеоморфизм отрезка [a₁, b₁] на отрезок и Аналогично Л. в произвольном топологич. пространстве Xопределяется параметрич. уравнением вида где - функция действительного переменного t, непрерывная на отрезке [ а, Ь], значения к-рой суть точки хпространства X.

Кроме такого подхода существует п другая точка зрения (К. Жордан, С. Jordan, 1882) на определение Л. параметрич. уравнениями: Л. наз. множество точек плоскости, координаты к-рыХ суть непрерывные функции параметра t, заданные на отрезке [a, b]; теперь точки, соответствующие различным значениям параметра, но имеющие одни и те же координаты, уже не считаются различными, и множество, составляющее Л., уже не рассматривается как упорядоченное значениями t. Это определение обобщается на любое топологич. пространство: множество точек топологич. пространства, являющееся непрерывным образом отрезка, наз. жордановой кривой.

Однако построены такие непрерывные функции и что множество точек, координаты к-рых определяются. этими функциями, заполняют квадрат (см. Пеано кривая). Более общо, всякий локально связный континуум (т. е. континуум, каждая точка к-рого обладает сколь угодно малой связной окрестностью) является непрерывным образом отрезка (теорема М а з у р к е в и ч а). Таким образом, не только квадрат, но и куб любого числа измерений и даже бесконечномерный гильбертов кирпич являются непрерывными образами отрезка.

Вышеизложенное показывает, что Л. не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений. Так, в дифференциальной геометрии эти ограничения выражаются в том, что на функции, фигурирующие в параметрическом задании Л., налагаются условия существования производных различных порядков. С другой стороны, существуют континуумы, которые естественно рассматривать как Л., но к-рые, не будучи локально связными, не являются непрерывными образами отрезка. Таков, напр., континуум, определяемый

условиями:

Общее определение Л. для случая плоскости было дано (Г. Кантор, G. Cantor, 1870-е гг.) в связи с созданием теории точечных множеств. Плоский континуум, в любой окрестности каждой точки к-рого имеются точки плоскости, не принадлежащие континууму, наз. канторовой кривой. Важный пример канторовой кривой доставляет ковер Серпиньского, строящийся следующим образом. Квадрат Qсо стороной 1 делят на девять равных квадратов прямыми, параллельными его сторонам, и удаляют все

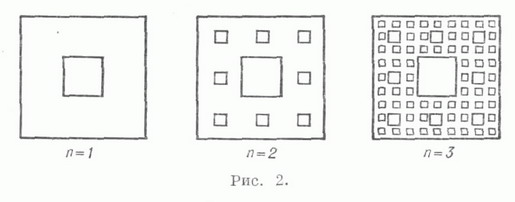
внутренние точки центрального квадрата (рис. 2,. n=1). Так же поступают и с каждым из оставшихся восьми квадратов первого ранга, получается 64 квадрата второго ранга (рис. 2, n = 2). Продолжая процесс для всех натуральных n, на n-м шаге получают 8ⁿ квадратов n- горанга со стороною Пересечение полученных таким образом множеств и есть ковер Серпинь-ского (рис. 2).

Какова бы ни была канторова кривая L, она может быть топологически вложена в ковер Серпиньского 5, т. е. в Sсодержится континуум L', гомеоморфный Л. L. Ковер Серпиньского является локально связным континуумом и потому может быть получен как непрерывный образ отрезка.

В топологии пользуются понятием Л., введенным в 1921 П. С. Урысоном и являющимся наиболее общим (но не чрезмерно). Определение Л. формулируется следующим образом: линией наз. одномерный континуум, т. с. связное компактное метрич. пространство С, каждая точка к-рого обладает сколь угодно малой окрестностью с границей размерности нуль. Другими словами, при любом e>0 пространство Сможет быть представлено в виде суммы конечного числа замкнутых множеств диаметра, меньшего е, обладающих тем свойством, что никакие три из этих множеств не имеют общей точки. Ковер Серпиньского удовлетворяет этому определению Л., так что всякая канторова кривая является также и Л. в смысле П. С. Урысона. Обратно, если плоский континуум является Л. в смысле П. С. Урысона, то он будет канторовой кривой. Определение Л., данное П. С. Урысоном, является внутренним: оно характеризуется лишь свойствами самого пространства С и не зависит от того, рассматривается ли это пространство само по себе или как подмножество другого топологич. пространства.

Существуют Л., к-рые не гомеоморфны никакому подмножеству плоскости. Такова, напр., Л., лежащая в трехмерном пространстве и состоящая из шести ребер тетраэдра и четырех отрезков, соединяющих какую-либо точку пространства, не лежащую ни на одной из его граней, с его вершинами (рис. 3). Но всякая Л. (в смысле П. С. Урысона) гомеоморфна нек-рому подмножеству трехмерного евклидова пространства (теорема М е н г е р а). Континуум М, обладающий тем свойством, что какова бы ни была Л.. С, в М найдется подконтинуум С', гомео-морфный континууму С, строится следующим образом. Куб К с ребром 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из куба Кудаляются центральный куб и все прилежащие к нему по двумерным граням кубы этого подразделения. Получается множество K₁, состоящее из 20 оставшихся замкнутых кубов первого ранга. Поступая точно так же с каждым из кубов первого ранга, получим множество K₂, состоящее из 400 кубов второго ранга (рис. 4). Продолжая этот процесс бесконечно, получим последовательность континуумов пересечение к-рых есть одномерный континуум М, паз. универсальной кривой М е н г е р а.

В исследовании Л. важную роль играет понятие индекса ветвления. Л. Св точке химеет индекс ветвления т, если каково бы ни было число e>0, существует открытое множество Uдиаметра, меньшего, чем е, содержащее точку х. граница к-рого есть множество мощности, не превосходящей т, но для достаточно малого e'>0 граница всякого открытого множества, содержащего точку х, диаметр к-рого меньше e', имеет мощность, не меньшую, чем т. Точки Л. относительно их индекса ветвления классифицируются следующим образом.

1) Точки с индексом ветвления п, п - натуральное.

2) Точки неограниченного индекса ветвления w. (Точка х Л. С имеет индекс ветвления со, если каково бы ни было число e>0, существует открытое множество, содержащее точку х, с диаметром, меньшим, чем е, граница к-рого состоит'из конечного множества точек; но каково бы ни было натуральное п, найдется такое e_n>0, что граница всякого открытого множества,

содержащего хи имеющего диаметр меньший, чем e_n состоит не менее, чем из га точек.)

3) Точки счетного индекса ветвления

4) Точки континуального индекса ветвления с.

Точка Л. С, индекс ветвления к-рой больше двух, наз. точкой ветвления; точка, индекс ветвления к-рой равен единице, наз. концевой точкой.

Примеры, а) Отрезок во всех своих внутренних точках имеет индекс ветвления, равный двум; индекс ветвления концов отрезка равен единице, б) Окружность в каждой своей точке имеет индекс ветвления два. в) Л., состоящая из га прямолинейных отрезков,.

исходящих из одной точки О, имеет в точке Оиндекс ветвления п. г) Л., состоящая из отрезков выходящих из начала координат О, имеющих длины и образующих с осью Ох углы, соответственно равные имеет в точке Онеограниченно возрастающий: индекс ветвления со (рис. 5). д) Л., состоящая из отрезка Оа ₀ длины 1 и отрезков длины 1, выходящих из точки Ои образующих с отрезком Оа ₀ углы, соответственно равные имеет в каждой точке отрезка Оа ₀ счетный индекс ветвления (рис. 6). е) Л., состоящая из отрезков, соединяющих точку Осо всеми точками канторова множества, лежащего на отрезке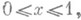

y=0, имеет во всех своих точках континуальный индекс ветвления с (рис. 7). ж) Ковер Серпиньского также имеет во всех своих точках континуальный индекс ветвления.

Если у Л. совсем нет точек ветвления, т. е. если в каждой точке Л. индекс ветвления равен 1 или 2, то эта Л. есть либо простая дуга - топологич. образ отрезка, либо простая замкнутая линия - топологич. образ окружности. При этом, если индекс ветвления Л. во всех точках равен 2, то это - простая замкнутая Л., если же у Л., не имеющей точек ветвления, есть концевые точки (при этом оказывается, что их непременно две), то она будет простой дугой. Если Л. имеет лишь конечное число точек ветвления, причем индекс ветвления каждой из них также конечен, то такая Л. может быть разбита на конечное число простых дуг, не имеющих попарно никаких других общих точек, кроме своих концов.

Окружность является единственной Л., все точки к-рой имеют один и тот же конечный индекс ветвления 2; других Л., имеющих во всех точках один и тот же конечный индекс ветвления, нет, более того, если все точки Л. Lимеют индекс ветвления больший или равный п, то на Л. Lнайдется точка, индекс ветвления к-рой больше или равен 2п-2, и при всяком натуральном псуществует Л., состоящая только из точек, имеющих индекс ветвления пи 2п-2 (теорема У р ы с о н а). Пример Л., состоящий только из точек с индексом ветвления 3 и 4, строится следующим образом. В равностороннем треугольнике со стороною 1 проводятся три средние линии, и из него выбрасываются внутренние точки треугольника, ограниченного средними Л. С каждым из оставшихся трех треугольников первого ранга проделывается аналогичная операция, в результате к-рой получается девять треугольников второго ранга. Поступая с ними так же, получим 27 треугольников третьего ранга и так далее для всякого натурального п. Пересечение полученных в результате выполнения этих операций множеств есть линия С(рис. 8). Л., состоящая из точек с индексом ветвления 3 и 4,- это два континуума С ₁ и С ₂, каждый из к-рых гомеоморфен Л. С и к-рые не имеют никаких других общих точек, кроме точек, соответствующих вершинам основного треугольника континуума С.

Существуют также Л., имеющие во всех своих точках неограниченный индекс ветвления, счетный индекс ветвления и континуальный индекс ветвления. Лит.:[1] Александров П. С., Введение в общую теорию множеств и функций, М.- Л., 1948; [2] К у р а т о в с к и й К., Топология, пер. с англ., т. 2, М., 1969; [3] М е n g е r К., Kurventheorie, Lpz.- В., 1932; [4] Пархоменко А. С., Что такое линия, М., 1954; [5] У р ы с о н П. С., Труды по топологии и другим областям математики, т. 2, М.- Л., 1951; [6] Хаусдорф Ф., Теория множеств, пер. с нем., М.- Д., 1937. А. С. Пархоменко.