Akademik

- топологическое Пространство X, В к-рол ДЛЯ любой точки и любой ее окрестности О _х существует меньшая окрестность такая, что для любых двух точек существует непрерывное отображение 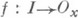единичного отрезка I=[0, 1] в окрестность Всякое Л. л. с. п. локально связно. Всякое открытое подмножество Л. л. с. п. локально линейно связно. Связное Л. л. с. п. является линейно связным пространством.

Л. л. с. п. играют важную роль в теории накрытий. Пусть - накрытие, а Y - Л. л. с. п. Тогда необходимым и достаточным условием того, чтобы отображение допускало поднятие, т. е. существовало такое отображение что f=pog, является выполнение соотношения

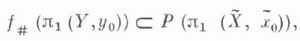
где я _х- фундаментальная группа. Если X - локально односвязное (локально 1-связное, см. ниже) пространство и то для любой подгруппы Нгруппы p₁(X, x₀) существует накрытие для к-рого

Многомерным обобщением локальной линейной связности является локальная k-связность (локальная связность в размерности k). Пространство Xназ. локально k-связным, если для любой точки 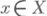и любой ее окрестности О _х существует такая меньшая окрестность что любое отображение r-мерной сферы S^r в U_x, где гомотопно в О _х постоянному отображению. Метрич. пространство X локально k-связно тогда и только тогда, когда всякое отображение с произвольного замкнутого подмножества Аметрич. пространства У с 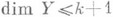можно продолжить на нек-рую окрестность Ав Y(теорема Куратовского - Дугунджи). С. А. Богатый.