Akademik

- 1) Первая теорема Нётер - теорема, устанавливающая связь между янфинитезимальными симметриями функционала вида

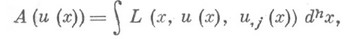
тде - независимые переменные,- функции, определенные в нек-рой области - их частные производные, L- нек-рая функция (функция Лагранжа), и законами сохранения для соответствующей системы уравнений Эйлера - Лагранжа

дающей необходимые условия экстремума функционала А. Именно, инфинитезимальной симметрии Z, т. е. векторному полю

к-рое порождает однопараметрич. группу преобразований, сохраняющую функционал А, соответствует закон сохранения

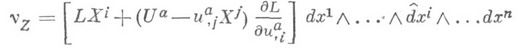
(где значок Щ означает пропуск соответствующего множителя), т. е. зависящая от функции и(х)(п-1)-форма, к-рая замкнута, если и(х)удовлетворяет уравнениям Эйлера - Лагранжа.

В теории поля n=4 координаты х интерпретируются как координаты пространства-времени, функционал Аназ. действием, а функция и(х)- полем. Поля и(х), доставляющие экстремум функционалу действия, соответствуют физически реализуемым полям с данной функцией Лагранжа. Если такое поле и(х)обращается в нуль на границе области D, то в силу теоремы Стокса интеграл от закона сохранения v по гиперповерхности 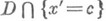не зависит от выбора числа с. В частности, если - коордпната времени, то этот интеграл дает величину, сохраняющуюся с течением времени.

Инвариантность функций Лагранжа различных фи-зич. полей относительно параллельных переносов и преобразований Лоренца (являющаяся следствием однородности и изотропности пространства-времени Мин-ковского) приводит по Н. т. к тензору энергии-импульса и тензору момента количества движения поля и к соответствующим им закопай сохранения энергии, импульса и момента количества движения. Инвариантность функционала действия электромагнитного поля относительно градиентных преобразований приводит к закону сохранения электрич. заряда. Аналогично из инвариантности лагранжиана того или иного поля относительно калибровочных преобразований получаются законы сохранения различных зарядов.

В классич. механике n=1 и координата х ¹ интерпретируется как время. Если функция Лагранжа не зависит явно от х ¹, то векторное поле является симметрией и Н. т. приводит к закону сохранения энергии. Для механич. системы, движение к-рой описывается движением по геодезическим нек-рой римановой метрики, симметриями соответствующего функционала действия будут кпллинговы поля. В этом случае закон сохранения, даваемый Н. т., геометрически означает, что величина проекции киллингова поля на направление геодезической постоянна вдоль этой геодезической. Общая современная формулировка Н. т. на языке расслоенных пространств состоит в следующем. Пусть - расслоение над n-мерным многообразием Мс фиксированной n-формой объема , а 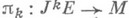- расслоение k-струй сечений расслоения 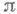. Если - локальные координаты в М, в к-рых форма имеет вид 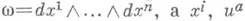- локальные координаты в Е, то в возникают локальные координаты - мультииндекс, Значение координаты на k-струе 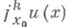сечения 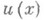расслоения равно

Гладкая функция определяет функционал действия А, сопоставляющий сечению число

Экстремальные для этого функционала сечения и(х)(в задаче с закрепленными концами) удовлетворяют уравнениям Эйлера - Лагранжа

- полные производные. Инфинитезимальный автоморфизм расслоения , т. е. векторное поле Z на Евида

наз. инфинитезимальной симметрией функционала А, если производная Ли от n-формы Лагранжа по направлению векторного поля , являющегося продолжением поля 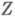на , равна нулю:

Для производной Ли справедлива следующая фундаментальная формула Нётер:

где .

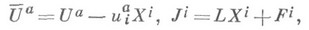
а 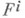- компоненты нек-рого векторного поля, зависящие от и их производных. В частности,при k=1. Если поле Zявляется инфинитезимальной симметрией, то

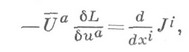
т. е. нек-рая линейная комбинация вариационных производных функции Лагранжа Lявляется дивергенцией векторного поля . В таком виде Н. т. впервые была сформулирована Э. Нётер (Е. Noether). Дивергенция поля J (наз. током Нётер) обращается в нуль на экстремалях функционала действия, а двойственная к нему (n-1)-форма , получающаяся из со внутренним умножением на J, замкнута, т. е. является законом сохранения.

Имеются важные обобщения Н. т. (см., напр., [5] - [7]). Они основаны на расширении понятия инфините-зимальной симметрии. Вместо векторных полей на Е, к-рым отвечают однопараметрич. группы преобразований, рассматриваются векторные поля на Е, коэффициенты к-рых зависят от сечений и(х)и их сколь угодно высоких производных. Такие поля Ууже не определяют никаких однопараметрич. групп преобразований, однако и для них можно чисто алгебраически определить понятие производной Ли. Поле Yназ. алгебраической инфинитезимальной симметрией, если производная Ли от формы Лагранжа по направлению этого поля равна нулю или, более общо, обращается в нуль на экстремалях функционала действия. Обобщенная теорема Нётер сопоставляет каждой алгебраич. симметрии закон сохранения. В применении к различным уравнениям математич. физики таким образом получается большое число новых важных законов сохранения.

2) Вторая теорема Нётер утверждает, что если функционал действия допускает бесконечномерную алгебру Ли инфинитезимальных симметрии, коэффициенты к-рых линейно зависят от рпроизвольных функций и их производных до порядка т, то вариационные производные функции Лагранжа Lудовлетворяют системе из рдифференциальных уравнений порядка т. Именно, если

есть инфинитезимальная симметрия при любых гладких функциях 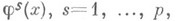то справедливы тождества

Эта теорема находит применения, напр., в теории калибровочных полей.

Первая и вторая Н. т. доказаны Э. Нётер (Е. Noether, 1918, см. [1]).

Лит.:[1] Нетер Э., в кн.: Вариационные принципы механики, М., 1959, с. 611-30; [2] Боголюбов Н. Н., Ширков Д. В., Введение в теорию квантованных полей, 2 изд., М., 1973; [3] Гельфанд И. М., Фомин С. В., Вариационное исчисление, М., 1961; [4] Арнольд В. И., Математические методы классической механики, М., 1974; [5] Овсянников Л- В., Групповой анализ дифференциальных уравнений, М., 1978; [6] Манив Ю. И., в кн.: Итоги науки и техники, Современные проблемы математики, т. 11, М., 1978, с. 5-152; [7] Виноградов А. М., "Докл. АН СССР", 1977, т. 236, №2, с. 284-87; [8] Лычагин В. В., "Успехи матем. наук", 1979, т. 34, в. 1, с. 137-65.

Д. В. Алексеевский.

3)Н. т. о нормализации: в любой конечно порожденной коммутативной целостной k-алгебре А, имеющей над полем kстепень трансцендентности d, найдутся такие dэлементов что Ацела над подалгеброй В, порожденной этими элементами. Если k-алгебра Аобладает градуировкой вида то элементы могут быть выбраны однородными.

Эта теорема (иногда называемая также леммой Нётер о нормализации) доказана Э. Нётер [1]; в градуированном случае она была сформулирована еще Д. Гильбертом [2].

Элементы алгебраически независимы над k, так что В- алгебра многочленов от переменных с коэффициентами из k. Если поле кбесконечно, то элементы можно выбрать из линейных комбинаций образующих алгебры Анад k. В случае алгебраически замкнутого поля кН. т. допускает следующую геометрич. формулировку: любое неприводимое аффинное d-мерное алгебраич. многообразие Xявляется конечнолистным (разветвленным) накрытием аффинного d-мерного пространства A^d, точнее, обладает конечным морфизмом на A^d. Более того, если X- замкнутое подмножество в kⁿ, то указанный морфизм может быть реализован как сужение на Xнек-рого линейного отображения пространства kⁿ на его d-мерное линейное подпространство.

Алгебра А, как B-модуль, конечно порождена. Подалгебра Ввыбирается неоднозначно, однако ряд свойств .В-модуля Ане зависят от ее выбора. Напр., если Аградуирована, как выше в условиях теоремы, а элементы однородны (так что Втоже градуирована), то свойство алгебры Абыть свободным B-модулем не зависит от выбора В.

Лит.:[1] Nоеthеr Е., "Math. Ann.", 1927, Bd 96, S. 26- 61; [2] Hilbert D., "Math. Ann", 1893, Bd 42, S. 313-73; [3] Атья М., Макдональд И., Введение в коммутативную алгебру, пер. с англ., М., 1972; [4] Бурбаки Н., Коммутативная алгебра, пер. с франц., М., 1971; [5] 3арисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1-2, М., 1963; [6] Ленг С, Алгебра, пер. с англ., М., 1968.

В. Л. Попов.