Akademik

- отображение одного множества на другое, каждое из к-рых наделено нек-рой структурой (алгебраич. операциями, топологией, отношением порядка). Общее определение О. совпадает с определением отображения или функции: пусть Xи Y - два множества; оператором Аиз множества Xво множество Yназ. правило или соответствие, к-рое каждому элементу хиз нек-рого подмножества 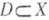сопоставляет однозначно определенный элемент 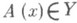; множество Dназ. областью определения оператора A и обозначается D (А);множество {(х),} наз. областью значений оператора A и обозначается R(A). Часто пишут Ах вместо (х). Термин "О." используется чаще всего в случае, когда Xи Y - векторные пространства. Если A - оператор из Xв Y, где Y=Х, то Аназ. оператором в X. Если D(A)=X, то Аназ. всюду определенным оператором. Если A₁, A_a- операторы из X₁ в Y₁ н из Х ₂ в Y₂ с областями

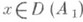определения D(A₁).и D(A₂) соответственно и такие, что i и A₁x=A₂x при всех , то при X₁= Х ₂, Y₁= Y₂ оператор А ₁ называется суженнем, или ограничением, оператора А ₂, а оператор A₂ - расширением оператора A₁; при , А ₂ называется расширением оператора A₁ с выходом из Х ₁.

Многие уравнения в функциональных или абстрактных пространствах можно представить в виде Ах-у, где , , 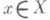у - задан, х - неизвестен, А - оператор из Xв Y. Утверждение о существовании решения такого уравнения при любой правой части 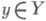равносильно утверждению, что область значении оператора Аесть все пространство Y; утверждение, что уравнение (х)=у имеет при любом 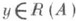единственное решение, означает, что Авзаимно однозначно отображает D(А).на R(А).

Если Xи Y - векторные пространства, то в множестве всех О. из Xв Y можно выделить класс линейных операторов;остальные О. из Xв Y наз. нелинейными операторами. Если Xи Y - топологические векторные пространства, то в множестве 0. из X в Y естественно выделяется класс непрерывных операторов, а также класс ограниченных линейных операторов A (таких операторов А, что образ любого ограниченного множества в Xограничен в У) и класс линейных компактных операторов (т. е. таких О., что образ любого ограниченного множества в Xпредкомпактен в Y). Если X и Y - локально выпуклые пространства, то в Xи Y естественно рассматривать различные тоцологии; О. наз. полунепрерывным, если он определяет непрерывное отображение пространства X(в исходной топологии) в пространство Y в слабой топологии (понятие полунепрерывности используется главным образом в теории нелинейных О.); О. наз. усиленно непрерывным, если он непрерывен как отображение пространства Xв ограниченно слабой топологии в пространство У; О. наз. слабо непрерывным, если он определяет непрерывное отображение X в Y, где X и Y наделены слабой топологией. Часто компактные О. наз. вполне непрерывными. Иногда термин "вполне непрерывный О." используется вместо термина "усиленно непрерывный О." или для обозначения О., переводящего любую слабо сходящуюся последовательность в сильно сходящуюся; если Xи Y - рефлексивные банаховы пространства, то эти условия эквивалентны компактности О. Если О. усиленно Непрерывен или компактен, то он непрерывен; если О. непрерывен, то он слабо непрерывен.

Графиком оператора Аназ. множество , определенное соотношением

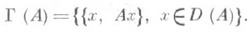
Пусть X и Y - топологические векторные пространства; оператор Аиз Xв Y наз. замкнутым оператором, если его график замкнут. Понятие замкнутого О. особенно плодотворно в случае линейных О. с плотной областью определения.

Понятие графика позволяет обобщить понятие О.: многозначным оператором из X в Y наз. любое подмножество Ав X x Y; если X и Y - векторные пространства, то многозначным линейным О. наз. линейное подпространство X x Y; областью определения многозначного О. наз. множество

D(А) = {х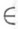X:существует 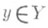такой, что {х, у} 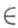А}.

Если X - векторное пространство над полем kи Y=k, то всюду определенный О. из Xв kназ. функционалом на X.

Если Х и Y - локально выпуклые пространства, то оператор A из X в Y с плотной в X областью определения имеет сопряженный оператор А* с плотной в Y* в ослабленной топологии областью определения тогда и только тогда, когда А - замкнутый О.

Примеры операторов. 1) О., сопоставляющий любому элементу 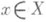элемент 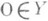(нулевой оператор).

2) О., сопоставляющий любому элементу 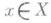этот же элемент (единичный оператор в Xобозначается id_X или 1_X).

3) Пусть X - векторное пространство функции на нек-ром множестве М и f - функция на М; О. в X с областью определения

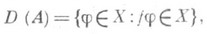
действующий по правилу

Aj=fj

при (А), наз. оператором умножения на функцию; А - линейный О.

4) Пусть X - векторное пространство функций на множестве Ми F - отображение множества Мв себя; О. в X с областью определения

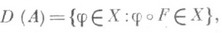
действующий но правилу

при (А), будет линейным О.

5) Пусть X, У - векторные пространства действительных измеримых функций на пространствах с мерой ( М,S_M, m) и (N,S_N n) соответственно, К-функция на Mx Nx , измеримая относительно произведения мер m x n x m₀> где m₀- мера Лебега на 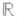, и непрерывная по при любых фиксированных 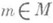, ; О. из Xв Y с областью определения

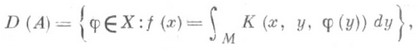
существующий для почти всех и 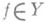, действующий по правилу Aj=f при 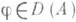, наз. интегральным оператором; если

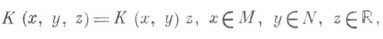
то Алинейный О.

6) Пусть X - векторное пространство функций на дифференцируемом многообразии М,x - векторное ноле на М;оператор Ав X с областью определения

D(А) = {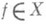:. производная D_xf функции f вдоль поля x определена всюду и D_xfX}, действующий по правилу Af=D_xf при 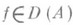, наз. оператором дифференцирования; A - линейный О.

7) Пусть X - векторное пространство функций на множестве М;всюду определенный О., сопоставляющий функции значение этой функции в точке 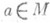, есть линейным функционал на X; он наз. d-функцией в точке а и обозначается d_a

8) Пусть G - коммутативная локально компактная группа, 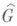- группа характеров группы G; dg, 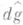- меры Хаара на G, 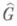соответственно; пусть

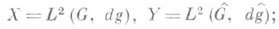
линейный оператор Аиз X в Y, сопоставляющий функции 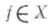функцию , определяемую формулой

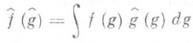
всюду определен, если сходимость интеграла понимается как сходимость в среднем.

Если Xи Y - топологические векторные пространства, то О. в примерах 1) и 2) непрерывны; если в примере 3) пространство Xесть L²(M,S_M, m), где m - мера на X, то О. умножения на ограниченную измеримую функцию замкнут и имеет плотную область определения; если в примере 5) пространство X=Y есть гильбертово пространство L²(M,S_M, m) и К( х, у,z) =K(x,y)z, где К( х, у).принадлежит L²(Mx M,S_M x S_M, m x m), то Акомпактен; если в примере 8) пространства X и Y рассматриваются как гильбертовы пространства, то Анепрерывен.

Если A - О. из Xв Y такой, что 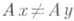при , , 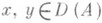то можно определить обратный оператор А ^-1 к А;вопрос о существовании обратного О. и его свойствах связан с теоремой существования и единственности решения уравнения Ax=f;если А ^-1 существует, то x=A^-1f при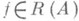

Для О. в векторных пространствах можно определить сумму, произведение на число и произведение О. Если А, В- операторы из Xв Y с областями определения D(А).и D(В).соответственно, то суммой операторов Аи Вназ. О., обозначаемый А+В, с областью определения

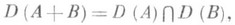
действующий по правилу

( А + В)x=Ах + Вх

при 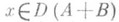. Произведением оператора A нa число lназ. О., обозначаемый lA, с областью определения

D(lA) = D(A), действующей по правилу (lА) х=l( Ах)

при . Произведение операторов определяется как композиция отображений: если Аоператор из X в Y, В - оператор из Y в Z, то произведением В к А наз. оператор ВА с областью определения

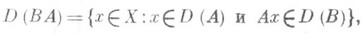
действующий по правилу

( ВА) х = В( Ах)

при

Если Р - всюду определенный О. в X такой, что РР=Р, то Рназ. проектором в Х; если I - всюду определенный О. в X такой, что II=id_X, то I наз. инволюцией в Х.

Теория О. составляет важнейшую часть линейного и нелинейного функционального анализа, являясь, в частности, основным аппаратом теории динамич. систем, представлений групп и алгебр и важнейшим матё-матич. инструментом математич. физики и квантовой механики.

Лит.:[1] Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965; [2] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981; [3] Канторович Л. В., Акилов Г. П., Функциональный анализ, 2 изд., М., 1977; [4]Данфорд Н., Шварц Дж. Т., Линейные операторы, пер. с англ., ч. 1-3, М.,,1962-74;[5] Эдвардс Р. -Э., Функциональный анализ, пер. с англ., М., 1969; [6] Иосида К., Функциональный анализ, пер. с англ., М., 1967.

М. А. Наймарк, А. И. Штерн.