Akademik

параллелогранник,- множество точек, радиус-векторы к-рых имеют вид

со всевозможными значениями Здесь a₁, а ₂, . . ., a_p - фиксированные векторы n-мерного аффинного пространства А. Они наз. образующими параллелотопа и совпадают с нек-рыми ребрами П. Все остальные ребра П. им параллельны. Если образующие П. линейно независимы (зависимы), то П. наз. р-мерным, или невырожденным (вырожденным). Вырожденный П. является параллельной проекцией нек-рого р-мерного П. на плоскость размерности 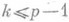. Невырожденный П. определяет несущую его р-мерную плоскость. Такой

П. при р=2 является параллелограммом, при р=3 - параллелепипедом.

Два невырожденных П. наз. параллельными, если параллельны несущие их плоскости. У параллельных П. можно сравнивать их р-мерпые "объемы" (хотя в пространстве Аможет и не быть метрики). Количественной характеристикой отношения р-мерного "объема" П. с образующими а ₁, а ₂, . . ., а _р к р-мерному "объему" параллельного П. с образующими b₁, b₂,. . ., b _р служит скаляр , где -матрица перехода от (b₁, b₂, . . ., b _р).к (a₁, а ₂, . . ., а _р), т. е.

Если в пространство Аопределено скалярное произведение, то квадрат р-мерного объема П. с образующими равен определителю -матрицы Грама с элементами .

Понятие П. тесно связано с понятием поливектора.

Лит.:[1] Широков П. А., Тензорное исчисление, Казань, 1961; [2] Беклемишев Д. В., Курс аналитической геометрии и линейной алгебры, 3 изд., М., 1976; [3] Пизо Ш., Заманский М., Курс математики. Алгебра и анализ, пер. с франц., М., 1971. Л. П. Купцов.