Akademik

внутреннее произведение ( а, b).ненулевых векторов a и b,- произведение их модулей на косинус угла j между ними: ( а, b) = | а || b| cos j. '

За j принимается угол между векторами, не превосходящий p. Если a=0 и b=0, то С. п. полагают равным нулю. С. п. (a, a)=a²=| а|² наз. скалярным квадратом вектора а. См. Векторная алгебра.

С. п. двух n-мерных векторов a=(a₁, a₂,... a_n) и b=(b₁, b₂, . . . b _п).в случае действительных координат наз. число

(a, b) = a₁b₁ + a₂b₂+...+a_nb_n, в случае комплексных координат - число

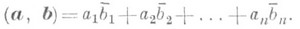
Бесконечномерное векторное пространство, в к-ром определено С. п. и выполнена аксиома полноты, наз. гильбертовым пространством. А. Б. Иванов.