многочлен f с коэффициентами из нек-рого поля или ассоциативно-коммутативного кольца Кс единицей, являющийся симметрической функцией от своих переменных, т. е. инвариантный при любых подстановках переменных:
 (*) С. м. образуют алгебру S( х 1, . . ., х п).над К.
(*) С. м. образуют алгебру S( х 1, . . ., х п).над К.
Важнейшие примеры С. м.- элементарные симметрические многочлены
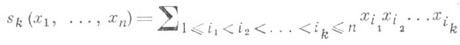
и степенные суммы, т. е. многочлены
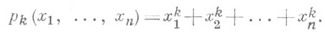
Для выражения степенных сумм р k( х 1, . . ., х п) в виде многочленов от элементарных симметрич. многочленов имеются рекуррентные формулы, называемые формулами Ньютона:
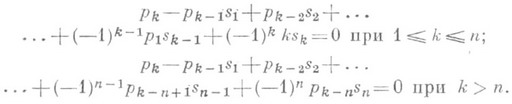
Элементарные С. м. от корней произвольного многочлена одной переменной со старшим коэффициентом 1 с точностью до знака совпадают с остальными коэффициентами этого многочлена (см. Виета теорема).
Основная теорема о симметрических многочленах: каждый С. м. является многочленом от элементарных С. м., причем представим в этом виде единственным образом. Другими словами, элементарные С. м. являются свободной системой образующих алгебры S( х 1, . . ., х п). Если поле имеет характеристику 0, то многочлены р 1, . . ., р п также являются системой свободных образующих алгебры S(x1, . .., хД).
Кососимметрическим, или знакопеременным, многочленом наз. многочлен f(x1 ,. . ., х п), удовлетворяющий соотношению (*), если подстановка p четная, и соотношению
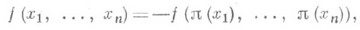
если p нечетная. Любой кососимметрич. многочлен представил: в виде Dng, где gесть С. м., а
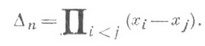
Это представление не однозначно, поскольку имеется соотношение
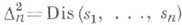
Лит.:[1] Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975; [2] Кострикин А. И., Введение в алгебру, М., 1977; [3] Мишина А. П., Проскуряков И. В., Высшая алгебра, 2 изд., М., 1965. О. А. Иванова.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.