Akademik

численные методы нахождения - методы вычисления полного спектра интегрального оператора или его части (чаще всего ставится задача отыскания одного-двух минимальных или максимальных по модулю собственных значений).
Сопутствующей задачей часто бывает задача приближенного численного нахождения собственных или, более общо, корневых функций данного интегрального оператора, соответствующих искомым собственным значениям. Наибольшее значение имеет задача нахождения собственных значений (и функций) линейного интегрального оператора Фредгольма.

Численные методы нахождения собственных значений интегральных операторов Фредгольма. Задача о собственных значениях и собственных функциях интегрального оператора Фредгольма заключается в нахождении таких комплексных чисел для к-рых существует нетривиальное (в данном функциональном классе) решение интегрального уравнения

В уравнении (1) К( х, s)- функция (или матрица-функция) двух групп переменных хи s такая, что интегральный оператор с ядром К - фредгольмов в рассматриваемом функциональном классе; D - область в евклидовом пространстве Функциональным классом может быть пространство С(D)непрерывных функций на D, или L₂(D) - квадратично интегрируемых функций на D,или другие функциональные пространства.
Основным приближенным способом решения задачи на собственные значения (1) является следующий. Выбирается нек-рая аппроксимация интегрального оператора в правой части (1) (см. Фредгольма уравнение;численные методы), напр., интеграл заменяется квадратурной формулой:

где s_i - узлы квадратурной формулы, - ее веса (см. [3] - [5]).
Вместо задачи (1) рассматривается задача на нахождение собственных значений и соответствующих корневых многообразий нек-рой матрицы, естественным образом связанной с аппроксимацией (2). Именно,

Для решения задачи (3) можно воспользоваться любыми методами нахождения собственных значений и векторов (более общо - корневых многообразий), разработанных в линейной алгебре (см. Линейная алгебра;численные методы). Найденные собственные значения и векторы алгебраич. задачи (3) будут близки к нек-рым собственным значениям и элементам основной задачи (1), если в определенном смысле близки операторы Аи Вместо (2) можно использовать и иные аппроксимации интегрального оператора. Основная задача (1) при этом редуцируется к алгебраич. задаче, аналогичной задаче (3). Исследование близости решений задач (1) и (3) проводится методами функционального анализа в рамках общей теории приближенных методов.
При этом задача на собственные значения (1) интерпретируется как задача нахождения собственных значений нек-рого вполне непрерывного оператора А, действующего в банаховом пространстве Ф:

Задача (3) интерпретируется как задача на собственные значения оператора близкого к А, но действующего, вообще говоря, в другом пространстве (связанном с Ф):

В общей теории приближенных методов доказываются различные теоремы о близости решений задач (4) и (5). В качестве примера подобных утверждений можно привести следующее. Пусть А _n- последовательность операторов действующих в Ф и

Тогда

где 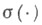- спектр соответствующих операторов. В этом случае каждое совпадает с Ф.
Большинство общих оценок близости собственных значений и элементов приближенной задачи (5) к собственным значениям (элементам) в задаче (4) не являются эффективными: эти оценки содержат постоянные, значения к-рых обычно не известны. Для контроля точности в таком случае можно использовать последовательность приближенных собственных значений (элементов), приближающуюся к искомому собственному значению (элементу) в (1) [или (4)]. Такую последовательность целесообразно строить, не используя непосредственно последовательность задач типа (5) с последовательно уточняющимся оператором т. к. этот путь приводит к весьма громоздким вычислениям. Вместо этого можно применять различные алгоритмы уточнения (напр., основанные на теории возмущений).

Обобщенные задачи о собственных значениях. В приложениях исследуются и более общие, чем (4) задачи о нахождении критич. параметров типа собственных значений. В абстрактной форме подобные задачи могут быть сформулированы следующим образом.

Требуется найти, при каких значениях параметра уравнение имеет более одного решения относительно ( А - некоторый нелинейный интегральный оператор в банаховом пространстве Ф, зависящий от комплексного параметра
В задаче (6) могут быть дополнительные ограничения на и на (напр., ищутся только такие к-рые удовлетворяют условию . задано и
С задачей (6) тесно связаны различные задачи о точках бифуркации в нелинейных интегральных уравнениях. Представляет интерес задача (6), в к-рой оператор линеен относительно но параметр входит не мультипликативно. Общая задача о точках бифуркации может быть редуцирована к такой форме. Кроме того, задача об отыскании собственных значений линейного оператора (1), лежащих в круге R - фиксирована, сводится к более общей задаче (6), в к-рой однако линейный по j оператор имеет конечномерную область значений. Действительно, пусть - интегральный оператор с вырожденным ядром, по норме близкий к А, причем Соотношение (1), определяющее собственные значения, может быть записано в виде:

Если то оператор обратим; собственные значения удовлетворяющие неравенству могут быть найдены из соотношения

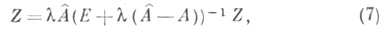
где Уравнение (7) эквивалентно (относительно Z) нек-рой системе линейных алгебраич. уравнений. Приравнивание к нулю ее определителя дает уравнение, корни к-рого являются собственными значениями интегрального оператора (1). Это рассуждение справедливо вообще для произвольного вполне непрерывного оператора . в банаховом пространстве Ф, если этот оператор допускает аппроксимацию по норме операторами с конечномерной областью значений. Конструкция (7) может быть использована для уточнения приближенно найденного собственного значения (и собственной функции).
Общая задача (6) может быть приближенно (аппроксимацией оператора А)сведена к конечномерной задаче типа (6). В случае более сложных задач рассматриваемого типа для отыскания собственных значений используется метод Монте-Карло (см. [7]).

Лит.:[1] Канторович Л. В., Крылов В. И., Приближенные методы высшего анализа, 5 изд., М.- Л., 1962; [2] Красносeльский М. А. [и др.], Приближенное решение операторных уравнений, М., 1969; [3] Березин И. С., Жидков Н. П., Методы вычислений, 2 изд., т. 2, М., 1962; [4] Крылов В. И., Бобков В. В., Монастырный П. П., Вычислительные методы, т. 2, М., 1977; [5] Мысовских И. П., лМетоды вычислений