Akademik

- 1) линейное представление группы или алгебры X в гильбертовом пространстве Нтакое, что Неймана алгебра в Нпорожденная семейством 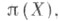является фактором. Если этот фактор имеет тип I (соответственно II, III, II₁, и т. д.), то Ф. наз. фактор представлением типа I и т. д.
2) Ф. группы или алгебры X - ее представление r, определяемое следующим образом. Пусть Е - (топологическое) векторное пространство представления представление есть представление в (топологическом) векторном пространстве E|F, являющимся факторпространством пространства Епо нек-рому инвариантному подпространству F представления определенное формулой 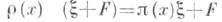для всех Если - непрерывное представление, то его Ф. также непрерывно.

А. И. Штерн.