- основные, исходные положения аналитич. механики, математически выраженные в форме вариационных соотношений, из к-рых как логпч. следствия вытекают дифференциальные уравнения движения, а также все положения и законы механики. В В. п. к. м. действительные движения материальной системы, происходящие под действием заданных сил, сравниваются с кинематически возможными движениями, допускаемыми наложенными на систему связями и удовлетворяющими определенным условиям. В большинстве случаев признаком, по к-рому действительное движение выделяется из рассматриваемого класса кинематически возможных движений, служит условие экстремальности (стационарности) нек-рой скалярной 'функции или функционала, обеспечивающее инвариантность описания.
В. п. к. м. отличаются один от другого как по форме и способам варьирования, так и по общности, но каждый из них, в рамках его приложимости, образует единую основу и как бы синтезирует всю механику соответствующих материальных систем. Иными словами, тот или иной из В. п. к. м. потенциально заключает в себе все содержание этой области науки и объединяет все ее положения в единой формулировке.
Классич. механика основывается на законах Ньютона, установленных для свободных материальных точек, и аксиомах связей. Справедливость В. п. к. м. доказывается, исходя из этих законов и аксиом. В свою очередь, любой из В. п. к. м. можно принять за аксиому и из нее логически вывести законы механики.
В. п. к. м. по форме подразделяются на дифференциальные и интегральные принципы. К дифференциальным принципам, характеризующим свойства движения для любого данного момента времени, относятся: принцип возможных перемещений, принцип Д'Аламбера - Лагранжа, принципы Гаусса, Герца, Четаева и Журдена. Интегральными принципами, характеризующими свойства движения на любых конечных промежутках времени, являются принципы наименьшего действия в формах Гамильтона - Остроградского, Лагранжа, Якоби и нек-рые др.
Первый пз В. п. к. м.- принцип возможных (виртуальных) перемещений, применялся еще Г. Галилеем (G. Galilei, 1665). Первым, кто понял общность этого принципа и его полезность для решения задач статики, был И. Бернулли (J. Bernoulli, 1717). Принцип получил обоснование, существенное развитие и применение в "Аналитической механике" Ж. Лагранжа (J. Lagrange, 1788), считавшего его основным для всей механики.
Этот принцип позволяет находить положения равновесия системы материальных точек, т. е. такие положения 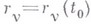 , в к-рых система будет оставаться все время, если она помещена в эти положения с нулевыми начальными скоростями
, в к-рых система будет оставаться все время, если она помещена в эти положения с нулевыми начальными скоростями  при условии, что
при условии, что 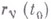 - возможные положения и
- возможные положения и 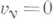 - кинематически возможные скорости при любом t. Здесь
- кинематически возможные скорости при любом t. Здесь  - радиус-векторы точек системы относительно начала Оинерциальиой системы координат
- радиус-векторы точек системы относительно начала Оинерциальиой системы координат  , причем
, причем 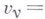
 ;
;  - возможные перемещения, допускаемые в данный момент времени наложенными на систему связями,
- возможные перемещения, допускаемые в данный момент времени наложенными на систему связями,  - заданные активные силы,
- заданные активные силы, 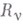 - реакции связей. Связи далее предполагаются идеальными и удерживающими, т. е.
- реакции связей. Связи далее предполагаются идеальными и удерживающими, т. е.
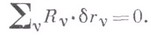
Принцип возможных перемещений: механич. система находится в равновесии в нек-ром положении тогда и только тогда, когда сумма элементарных (бесконечно малых) работ активных сил на всяком возможном перемещении, выводящем систему из рассматриваемого положения, равна нулю

в любой момент времени.
Уравнение (1) является общим уравнением статики, сводящим любую задачу статики к математич. задаче исследования этого уравнения. Для частного случая потенциальных сил

где TV - число точек системы, равенство (1) принимает вид ,

при любом t, т. е. механич. система, подверженная действию потенциальных сил, находится в равновесии тогда и только тогда, когда силовая функция имеет стационарное значение.
Для вывода уравнений динамики методами статики применяется так наз. принцип Д'Аламбера: если к действующим на точки материальной системы заданным (активным) силам и силам реакций связей присоединить силы инерции -  , то такая система сил будет находиться в равновесии. Здесь
, то такая система сил будет находиться в равновесии. Здесь 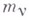 - масса
- масса  -и точки,
-и точки,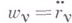 - ее ускорение. Обобщение принципа Д'Аламбера и принципа возможных перемещений было получено Ж. Лагранжем (1788).
- ее ускорение. Обобщение принципа Д'Аламбера и принципа возможных перемещений было получено Ж. Лагранжем (1788).
Принцип Д'Аламбера - Лагранжа: для действительного движения системы сумма элементарных работ активных сил п сил инерции на любых возможных перемещениях равна нулю:
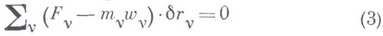
в любой момент времени.
В принципе Д'Аламбера - Лагранжа сравниваются положения системы в ее действительном движении с бесконечно близкими положениями, допускаемыми связями в рассматриваемый момент времени. Соотношение (3) определяет зависимость между активными силами, вызываемыми ими при наложенных связях ускорениями и возможными перемещениями. Выражая необходимое и достаточное условие соответствия действительного движения, являющегося одним из кинематически возможных движений, заданным активным силам, уравнение (3) является общим уравнением динамики. Когда все ускорения  уравнение (3) принимает вид (1) общего уравнения статики.
уравнение (3) принимает вид (1) общего уравнения статики.
Уравнения движений содержатся в уравнении (3). Для получения полной системы независимых дифференциальных уравнений динамики достаточно выразить возможные перемещения  через систему независимых перемещений и подставить в уравнение (3). Таким путем могут быть получены, напр., уравнения Лагранжа, Аппеля и любая другая система независимых дифференциальных уравнений движения. Если же из семейства возможных перемещений выделить к.-л. одно перемещение и подставить его в уравнение (3), то полученное соотношение будет являться или одним из диф-ференцпальных уравнений движения системы или следствием из них. Таким способом можно получить, например, общие теоремы (законы) динамики: о количестве движения, моменте количеств движения, кинетической энергии.
через систему независимых перемещений и подставить в уравнение (3). Таким путем могут быть получены, напр., уравнения Лагранжа, Аппеля и любая другая система независимых дифференциальных уравнений движения. Если же из семейства возможных перемещений выделить к.-л. одно перемещение и подставить его в уравнение (3), то полученное соотношение будет являться или одним из диф-ференцпальных уравнений движения системы или следствием из них. Таким способом можно получить, например, общие теоремы (законы) динамики: о количестве движения, моменте количеств движения, кинетической энергии.
Общие теоремы динамики системы характеризуют нек-рые свойства движения, но, в отличие от В. п. к. м., ни одна из них в общем случае не в состоянии заменить всю систему дифференциальных уравнений движения и вполне охарактеризовать движение системы.
Принцип Д'Аламбера - Лагранжа является одним из наиболее общих В. п. к. м., справедливым как для голономных, так и для неголономных систем. Все другие В. п. к. м. представляют собой или иные формулировки этого принципа или следствия из него. Принцип Д'Аламбера - Лагранжа не связан, однако, с понятием экстремума к.-л. функции. В нем фигурирует бесконечно малая величина - сумма элементарных работ заданных сил и сил инерции на бесконечно малом возможном перемещении из заданной конфигурации, не представляющая собой вариации к.-л. функции, подобно равенству (2).
К. Гаусс (С. Gauss, 1829) предложил новый вариационный принцип, представляющий собой модификацию принципа Д'Аламбера-Лагранжа. Среди всех кинематически возможных движений рассматриваются мыслимые по Гауссу движения, удовлетворяющие условиям, наложенным на систему связей, и условием постоянства  и
и  для рассматриваемого момента времени t. В момент
для рассматриваемого момента времени t. В момент 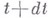

где 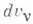 и
и  обозначают изменения скоростей за промежуток времени
обозначают изменения скоростей за промежуток времени 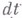 для действительного и к.-л. мыслимого движений; при этом уравнение (3) приводится к виду
для действительного и к.-л. мыслимого движений; при этом уравнение (3) приводится к виду

причем 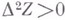 .
.
Принцип наименьшего принуждения (Гаусса принцип): движение системы материальных точек, связанных между собой произвольным образом и подверженных любым влияниям, в каждое мгновение происходит в наиболее совершенном, какое только возможно, согласии с тем движением, каким обладали бы эти точки, если бы они стали свободными, т. е. движение происходит с наименьшим возможным принуждением, если в качестве меры принуждения за время dt принять величину Z, равную сумме произведений массы каждой точки на квадрат величины ее отклонения от того положения, которое она заняла бы, если бы была свободной. Иначе говоря, в каждый момент времени tсреди всех ускорений, обусловленных связями, действительными ускорениями 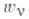 различных точек системы будут те, которые обращают в минимум функцию Z второй степени относительно ускорений.
различных точек системы будут те, которые обращают в минимум функцию Z второй степени относительно ускорений.
Равновесие является частным случаем общего закона: оно имеет место в том случае, когда точки не имеют скорости и когда сохранение системы в состоянии покоя более близко к свободному движению в случае упразднения связей, чем к возможным движениям, допускаемым связями.
Из принципа Гаусса при выражении Z через независимые ускорения системы получаются уравнения Аппеля. Принцип Гаусса представляет собой физич. аналогию предложенному К. Гауссом наименьших квадратов методу теории ошибок. Принцип Гаусса эквивалентен принципу Д'Аламбера - Лагранжа, однако при рассмотрении нелинейных дифференциальных связей вида  эти принципы по П. Аппелю (P. Appell) и Э. Делассю (Е. Delassus, 1911-13) оказались несовместимыми. Этот вопрос был разрешен Н. Г. Четаевым (1932 - 33), предложившим определять возможные перемещения для нелинейных связей условиями вида
эти принципы по П. Аппелю (P. Appell) и Э. Делассю (Е. Delassus, 1911-13) оказались несовместимыми. Этот вопрос был разрешен Н. Г. Четаевым (1932 - 33), предложившим определять возможные перемещения для нелинейных связей условиями вида
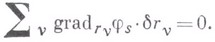
Из принципа Гаусса следует принцип наименьших реакций: для действительного движения величина

есть минимум. Принцип Гаусса обобщен на случай освобождения системы от части связей. Так как возможные перемещения исходной системы находятся среди возможных перемещений освобожденной системы, то справедливо соотношение:
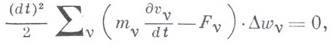
где  - изменение скорости за время dt в освобожденном движении. Это уравнение с учетом (4) можно привести к виду
- изменение скорости за время dt в освобожденном движении. Это уравнение с учетом (4) можно привести к виду

где

характеризует меру отклонения движения 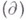 от движения
от движения  за время
за время  . Аналогично записываются
. Аналогично записываются  и
и  Из уравнения следуют неравенства
Из уравнения следуют неравенства
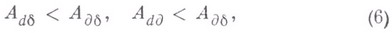
выражающие теорему: отклонение действительного движения 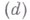 системы от мыслимого
системы от мыслимого  [освобожденного действительного
[освобожденного действительного  ] движения меньше отклонения движения
] движения меньше отклонения движения  от движения
от движения  . Эта теорема доказана Н. Г. Четаевым (1932 - 33). Теорема, выражаемая вторым из неравенств (6), для случая линейных неголономных связей высказана Э. Махом (Е. Mach, 1883) и доказана Е. А. Болотовым (1916).
. Эта теорема доказана Н. Г. Четаевым (1932 - 33). Теорема, выражаемая вторым из неравенств (6), для случая линейных неголономных связей высказана Э. Махом (Е. Mach, 1883) и доказана Е. А. Болотовым (1916).
К принципу Гаусса тесно примыкает принцип прямейшего пути, постулированный Г. Герцем (Н. Hertz., 1894) в качестве основного закона разработанной нм механики, в которой, в отличие от механики Ньютона, вместо понятия силы введены представления о скрытых связях, скрытых массах и скрытых движениях.
Принцип прямейшего пути (наименьшей кривизны принцип, Герца принцип): всякая свободная система пребывает в своем состоянии покоя или равномерного движения вдоль прямейшего пути. Под свободной системой Г. Герц понимает систему, не подверженную действию активных сил и стесненную только внутренними связями, накладывающими условия лишь на взаимное расположение точек системы. Прямейший путь определяется как такая траектория, элементарные дуги к-рой обладают наименьшей кривизной по сравнению с любыми другими" дугами, допускаемыми связями и имеющими с рассматриваемой элементарной дугой общие начальную точку и касательную в ней, причем величина Z интерпретируется как кривизна траектории точки, изображающей положение системы в ЗN-мерном евклидовом пространстве с прямоугольными координатами
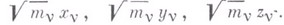
Иными словами, принцип Герца утверждает, что среди всех совместимых со связями траекторий действительная траектория обладает наименьшей кривизной.
Принцип Герца эквивалентен принципу Гаусса для систем, стесненных стационарными связями и не подверженных действию активных сил. Н. Г. Четаев (1941) предложил следующее видоизменение принципа Гаусса.
Принцип максимума работы (принцип Четаева): работа

на элементарном цикле, состоящем из прямого движения в поле заданных сил и движения обратного в поле сил, к-рых было бы достаточно для создания действительного движения, если бы механич. система была совершенно свободной; для действительного движения имеет (относительный) максимум в классе мыслимых по Гауссу движений. Принцип Чатаева позволяет расширить характер обычно рассматриваемых механич. систем путем привлечения принципа Карно из термодинамики.
Изложенные принципы по способам-варьирования подразделяются на две группы: в принципах возможных перемещений и Д'Аламбера - Лагранжа варьируется в нек-рый момент времени положение 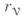 системы, aв принципах Гаусса, Герца и Четаева варьируются ускорения
системы, aв принципах Гаусса, Герца и Четаева варьируются ускорения 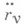 системы при постоянных
системы при постоянных  и
и 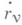 . Промежуточное место между этими двумя группами занимает принцип Журдена, в к-ром в момент tварьируются скорости
. Промежуточное место между этими двумя группами занимает принцип Журдена, в к-ром в момент tварьируются скорости  при постоянных
при постоянных 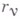 . В момент
. В момент  возможные перемещения
возможные перемещения 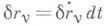 , и уравнение (3) принимает вид:
, и уравнение (3) принимает вид:

В интегральных В. п. к. м. сравнение действительного и кинематически возможных движений производится для конечных промежутков времени. Именно, сравниваются значения нек-рых определенных интегралов (наз. действием), вычисляемых для действительного и кинематически возможных движений, удовлетворяющих определенным условиям, между нек-рыми двумя конечными положениями системы. Интегральные В. п. к. м. менее общи по сравнению с дифференциальными принципами и применимы гл. обр. к голоном-ным системам, находящимся под действием потенциальных сил. Наиболее общим из них является принцип, установленный У. Гамильтоном (W. Hamilton, 1834 - 35) для случая стационарных голономных связей н обобщенный М. В. Остроградским (1848) на нестационарные геометрич. связи. Пусть известны положения 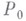 н
н 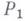 голономной системы в моменты времени
голономной системы в моменты времени 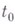 и
и  в нек-ром ее действительном движении под действием заданных сил и сил реакций. В этом движении
в нек-ром ее действительном движении под действием заданных сил и сил реакций. В этом движении 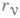 будут функциями времени, к-рые удовлетворяют связям н принимают для
будут функциями времени, к-рые удовлетворяют связям н принимают для  н
н  значения, отвечающие положениям
значения, отвечающие положениям 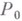 и
и  . Пусть
. Пусть  - нек-рые функции времени класса
- нек-рые функции времени класса  , достаточно близкие к
, достаточно близкие к 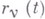 , удовлетворяющие связям н принимающие для
, удовлетворяющие связям н принимающие для  и
и  те же значения, что и
те же значения, что и  . При этом
. При этом  уничтожаются при
уничтожаются при 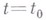 и
и  и. имеют смысл возможных перемещений. Если считать
и. имеют смысл возможных перемещений. Если считать 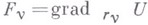 , то
, то

где функционал Sназ. действием по Гамильтону за промежуток времени  .
.
Принцип стационарного действия (принцип Гамильтона - Остроградского): в действительном движении системы действие по Гамильтону имеет стационарное значение по сравнению с любыми бесконечно близкими кинематически возможными движениями, для к-рых начальное и конечное положения системы одинаковы с соответствующими положениями для действительного движения и время движения одинаково. В случае непотенциальных сил принцип Гамильтона - Остроградского выражается уравнением
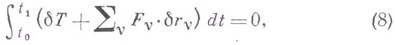
т. е., если 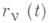 - функции времени, соответствующие действительному движению системы, то интеграл в (8) равен нулю для всех вариаций функций
- функции времени, соответствующие действительному движению системы, то интеграл в (8) равен нулю для всех вариаций функций 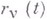 , совместимых со связями п уничтожающихся на обоих пределах интеграла.
, совместимых со связями п уничтожающихся на обоих пределах интеграла.
Равенства (7) и (8) представляют собой необходимые и достаточные условия для действительности движения системы под действием заданных сил. Уравнение (8) справедливо и для неголономных систем, однако для последних движение 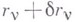 не является, вообще говоря, кинематически возможным; уравнение (7) несправедливо для неголоиомных систем.
не является, вообще говоря, кинематически возможным; уравнение (7) несправедливо для неголоиомных систем.
Если уравнения геометрич. связей представить в виде
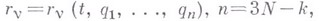
где  - число связей, и ввести функцию Лагранжа
- число связей, и ввести функцию Лагранжа

то

При этом в расширенном 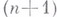 -мерном координатном пространстве
-мерном координатном пространстве  равенство (7) соответствует обычной (непараметрической) задаче вариационного исчисления при закрепленных концах. В
равенство (7) соответствует обычной (непараметрической) задаче вариационного исчисления при закрепленных концах. В 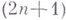 мерном расширенном фазовом пространстве с координатами
мерном расширенном фазовом пространстве с координатами  равенство (7) соответствует вариационной задаче со свободными концами (
равенство (7) соответствует вариационной задаче со свободными концами ( и
и  ) фиксированы,
) фиксированы, 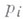 - свободны), причем
- свободны), причем
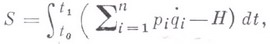
где 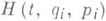 - функция Гамильтона. Из уравнения (7) выводятся уравнения Лагранжа:
- функция Гамильтона. Из уравнения (7) выводятся уравнения Лагранжа:

и канонич. уравнения Гамильтона:

Для решения основной задачи динамики достаточно знания функции действия
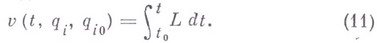
Однако для определения функции действия по формуле (11) необходимо знание закона движения. Чтобы обойти эту трудность, У. Гамильтон нашел дифференциальное уравнение
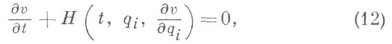
к-рому удовлетворяет функция действия. К. Якоби (С. Jacobi, 1837) показал, что если известен полный интеграл  уравнения (12), зависящий от ппроизвольных постоянных
уравнения (12), зависящий от ппроизвольных постоянных  , из к-рых ни одна не является аддитивной, то общее решение уравнений (10) дается равенствами:
, из к-рых ни одна не является аддитивной, то общее решение уравнений (10) дается равенствами:

где  - произвольные постоянные.
- произвольные постоянные.
Для систем, стесненных стационарными связями и находящихся под действием потенциальных сил, не зависящих явно от времени, существует интеграл энергии

Его существование позволяет ограничить множество сравниваемых кинематически возможных движений, переводящих систему из положения 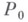 в положение
в положение  , движениями, при к-рых полная механич. энергия Еимеет одно и то же фиксированное значение Л. В этом случае интеграл (13) можно рассматривать как неголономное условие и искать принцип механики в виде условного вариационного принципа. Эту задачу разрешил Ж. Лагранж (1760).
, движениями, при к-рых полная механич. энергия Еимеет одно и то же фиксированное значение Л. В этом случае интеграл (13) можно рассматривать как неголономное условие и искать принцип механики в виде условного вариационного принципа. Эту задачу разрешил Ж. Лагранж (1760).
Принцип стационарного действия Лагранжа: если заданы начальный момент времени t0 и начальное и конечное положения голономной системы, для к-рой существует интеграл энергии, то для действительного движения

по сравнению с варьированными движениями между теми же начальным и конечным положениями и с той же энергией  , что и в действительном движении. Символ
, что и в действительном движении. Символ 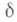 - вариация при условии (13).
- вариация при условии (13).
Выполнение соотношения (13) при постоянном 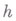 для всех сравниваемых в принципе Лагранжа движений налагает определенные ограничения на скорости этих движений и время движения из положения
для всех сравниваемых в принципе Лагранжа движений налагает определенные ограничения на скорости этих движений и время движения из положения 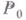 в положение Р 1 зависит от кривой, по к-рой совершается движение. Таким образом, принцип Лагранжа (14) [с учетом (13)] представляет собой условную вариационную задачу с верхним свободным концом.
в положение Р 1 зависит от кривой, по к-рой совершается движение. Таким образом, принцип Лагранжа (14) [с учетом (13)] представляет собой условную вариационную задачу с верхним свободным концом.
Для рассматриваемых систем исключением времени tиз(14) с помощью интеграла энергии (13) К. Якоби (1837) получил новый В. п. к. м.
В обобщенных координатах  кинетич. энергия системы
кинетич. энергия системы

Пусть заданы метрика координатного пространства формулой

а также конечные положения системы Р 0 и Р 1 в нек-ром действительном движении системы.
Принцип стационарного действия Якоби: если заданы начальное и конечное положения голономной консервативной системы, то для действительного движения

при сравнении со всякими другими бесконечно близкими движениями между теми же самыми начальным и конечным положениями и с тем же самым постоянным значением энергии k, что и в действительном движении. Принцип Якоби приводит задачу изучения движения голономной консервативной системы к геометрич. задаче отыскания в римановом пространстве с метрикой (15) экстремалей вариационной задачи (16), к-рые представляют собой действительные траектории системы. Принцип Якоби выявляет тесную связь, существующую между движениями голономной консервативной системы и римановой геометрией пространства. Если дви- . жение системы происходит в отсутствие заданных сил, когда  , то система движется вдоль геодезич. линии координатного пространства
, то система движется вдоль геодезич. линии координатного пространства  с постоянной скоростью. Этот факт является обобщением закона инерции Галилея. Когда
с постоянной скоростью. Этот факт является обобщением закона инерции Галилея. Когда  ,
,
разыскание движения голономной консервативной системы также сводится к задаче определения геодезических в римановом пространстве с метрикой
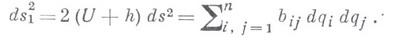
Для случая одной материальной точки, когда линейный элемент 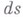 - элемент евклидова 3-мерного пространства, принцип Якоби представляет собой механич. аналог принципа Ферма в оптике.
- элемент евклидова 3-мерного пространства, принцип Якоби представляет собой механич. аналог принципа Ферма в оптике.
Уравнения Лагранжа (9) или уравнения экстремалей вариационных принципов Гамильтона - Остроградского, Лагранжа и Якоби являются необходимыми условиями экстремума соответствующего интеграла, или действия по Гамильтону, Лагранжу, Якоби. В случаях, когда выполняются достаточные условия минимума, эти интегралы в действительных движениях принимают минимальные значения. Вследствие этого интегральные В. п. к. м. наз. также принципами наименьшего действия.
Использование интегральных В. п. к. м. естественным образом приводит к понятию обобщенных решений и расширению классов функциональных пространств, в к-рых разыскиваются решения задач математич. физики.
В. п. к. м. оказались применимыми не только к дискретным материальным системам, но и к системам с распределенными параметрами, к сплошным средам; они играют важную роль в теории поля и в математич. физике. С В. п. к. м. тесно связаны оптико-механич. аналогия, теория канонич. преобразований, теория групп Ли и законы сохранения. В. п. к. м. обладают большой эвристической ценностью, они распространены и на другие области физики, в частности на теорию относительности и на квантовую и волновую механику, где важную роль играют принципы наименьшего действия и связанный с ними лаграяжев и гамильтонов математич. формализм.
Лит.:[1] Аппель П., Теоретическая механика, 6 изд. .т. 2, пер. с франц., М., 1960; [2] Болотов Е. А., О принципе Гаусса, "Изв. физ.-матем. об-ва при Казан, ун-те. Сер. 2", 1916, т. 21, .№ 3, с. 99-152; [3] Вариационные принципы механики, сб. статей, М., 1959; [4] Ланцош К., Вариационные принципы механики, пер. с англ., М., 1965; [5] Парс Л. А., Аналитическая динамика, пер. с англ., М., 1971; [6] Розе Н. В., Лекции по аналитической механике, ч. 1, Л., 1938; [7] Четае в Н. Г., Устойчивость движения. Работы по аналитической механике, М., 1962. В. В. Румянцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.