Akademik

- основная операция внешней алгебры тензоров, определенных в n-мерном векторном пространстве Vнад полем К.

Пусть - базис V, а и b - р - и q-формы:

Внешнее произведение форм а и b есть (p+q)-форма с, получающаяся альтернацией тензорного произведения . Форма собозначается ; она имеет кососимметрические координаты

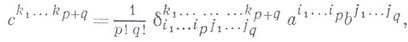
где 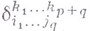- компоненты обобщенного Кронекера символа. Аналогично определяется В. п. ковариантных тензоров.

Основные свойства В. п.:

1) 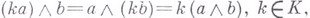- однородность,

2) - дистрибутивность,

3) i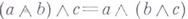 - ассоциативность.

4) если характеристика поля Котлична от двух, то для формы анечетной валентности

В. п. sвекторов наз. разложимым s-вектором. Каждый поливектор размерности sесть линейная комбинация разложимых s-векторов. Компоненты разложения являются 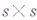-минорами -матрицы 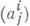, коэффициентов векторов При их В. п. имеет вид:

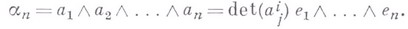
Над полями характеристики, отличной от двух, равенство необходимо и достаточно для линейной зависимости векторов . Ненулевой разложимый s-вектор 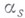определяет в V s -мерное ориентированное подпространство А, параллельное векторам и параллелотоп, лежащий в Аи образованный векторами выходящими из одной точки (этот параллелотоп обозначается через ). Условия и 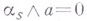эквивалентны.

Лит. см. при статье Внешняя алгебра. Л. П. Купцов.