Akademik

раздел геометрии, изучающий те свойства поверхности и фигур на ней, к-рые зависят лишь от длин кривых, лежащих на поверхности, и тем самым могут быть определены без обращения к объемлющему пространству. К В. г. регулярных поверхностей относятся такие понятия, как, напр., угол между кривыми, площадь области, полная (или гауссова) кривизна поверхности, геодезическая кривизна кривой, Леви-Чивита связность. Термин "В. г." употребляется и в более общей ситуации для обозначения структуры (обычно метрики или связности), индуцированной в топология, пространстве его отображением в другое пространство, априори наделенное аналогичной структурой.

Возможность рассматривать объекты В. г. как свойства самой поверхности, безотносительно к погружению ее в пространство, привела к исследованию абстрактных пространств с внутренней метрикой, свойства к-рых сходны с В. г. поверхностей (см. Риманово пространство, Выпуклая поверхность, Двумерное многообразие ограниченной кривизны). Наряду с внутренним подходом возможно выделение классов погруженных поверхностей и подмногообразий по их внешнегеометрич. свойствам. Сравнение этих двух подходов составляет проблему изометрических погружений и вложений. В ряде важных случаев оба подхода приводят к одним и тем же классам метрик. Напр., любая риманова метрика (класса 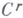, 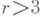) может рассматриваться как В. г. нек-рого подмногообразия евклидова пространства достаточно большой размерности, любая полная двумерная внутренняя метрика неотрицательной кривизны - как В. г. выпуклой поверхности в . Клас-сич. пример противоположной ситуации представляет Гильберта теорема о несуществовании регулярного изометрич. погружения плоскости Лобачевского в Термин "В. г.", отнесенный к подобного рода абстрактным пространствам, обретает смысл только в противопоставлении внешней геометрии в рамках к.-л. определенной теории. Выяснение связей между В. г. поверхностей и ее внешней геометрии составляет одну из наиболее трудных и содержательных задач геометрии. Сюда наряду с проблемой изометрич. погружений относятся, напр., следующие вопросы: изгибание поверхностей, бесконечно малые изгибания, однозначная определенность поверхности ее метрикой, влияние гладкости метрики на гладкость поверхности. Рассматривались также соотношения между внешней и В. г. при суперпозиции погружений (кривые на поверхности, минимальные подмногообразия сфер).

Основы В. г. созданы К. Гауссом (С. Gauss) (см. [1]). Они развиты в многомерном случае Б. Риманом (В. Hiemann) (см. [2]), а в нерегулярном случае А. Д. Александровым (см. [3]).

Лит.:[1] Гаусс К., Общие исследования о кривых поверхностях, пер. с лат., в сб.: Об основаниях геометрии, М. _г 1956; [2] Риман В., О гипотезах, лежащих в основании геометрии, пер. с нем., там же, с. 309-11: [3] Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М.-Л., 1948. Ю. Д. Бурого.