Akademik

на фоне помех - один из разделов статистической теории связи. Математически задачи В. с. суть статистич. задачи теории случайных процессов (см. также Информации теория). Ниже приведены нек-рые типичные задачи теории В. с.

Переданный сигнал s(t), случайная или неслучайная функция известной структуры, превращается в принятый сигнал , , где n(t).- случайный процесс (шум), а V(канал связи) - нек-рый оператор, преобразующий пару (s, n).в принятый сигнал х. Чаще всего предполагается, что шум действует на сигнал аддитивно: . В последней ситуации задачи В. с. следующие.

1) Обнаружение сигнала - проверка гипотезы (наличие сигнала) против альтернативы (отсутствие сигнала). Рассматриваются также более сложные варианты исходной гипотезы: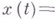 начиная с нек-рого момента - момента появления сигнала. При этом возникает задача оценки .

2) Различение сигналов - проверка гипотезы против гипотезы , где - два различных множества сигналов.

3) Фильтрация (восстановление сигнала) - отыскание статистических оценок для значений сигнала в точке tпо реализации

См. также Статистическая гипотеза, Случайных процессов фильтрация.

Лит.:[1] Давенпорт В., Рут В., Введение в теорию случайных сигналов и шумов, пер. с англ., М., 1960; [2] Харкевич А. А., Борьба с помехами, 2 изд., М., 1965.

И. А. Ибрагимов.