Akademik

В физике принято различать четыре типа фундам. вз-ствий: сильное, эл.-магн., слабое и гравитационное. Соотв. существуют четыре класса элем. ч-ц: адроны, к-рые участвуют во всех типах вз-ствий (они делятся на барионы и мезоны); лептоны, не участвующие только в сильном вз-ствии (из них нейтрино не участвуют и в эл.-магн. вз-ствии); фотон, участвующий только в эл.-магн. вз-ствии; гипотетич. гравитон — переносчик гравитац. вз-ствия. Каждая группа ч-ц характеризуется своими специфич. законами сохранения. Так, с большой точностью установлено сохранение барионного и электрич. зарядов, электронного и мюонного лептонных зарядов (по отдельности). Кроме того, в сильном вз-ствии имеются приближённые законы сохранения — изотопич. спина, странности, «очарования» и т. д., к-рые нарушаются эл.-магн. и (или) слабым вз-ствиями. Каждый из законов сохранения явл. проявлением определённой внутр. симметрии ур-ний поля (ур-ний движения). Если, напр., каким-то образом удалось бы «выключить» эл.-магн. и слабое вз-ствия, то оказалось бы, что протон и нейтрон неотличимы. А т. к. протон и нейтрон — квант. объекты, описываемые волн. ф-циями yp (r, t) и yn(r, t), то невозможно различить не только эти ч-цы, но и любую их суперпозицию, к-рую можно изобразить как поворот на нек-рый угол в т. н. изотопич. пр-ве (подобно тому как единичный вектор в плоскости можно задавать как его проекциями на оси х и у («р» и «n»), так и углом поворота j по отношению к оси х). Это и есть внутр. симметрия ур-ний, к-рая соответствует сохранению изотопич. спина (см. ИЗОТОПИЧЕСКАЯ ИНВАРИАНТНОСТЬ). Допустим, что в нек-рой лаборатории протоном называют ч-цу, состояние к-рой описывается одной суперпозицией волн, ф-ций yp и yn, а в др. лаборатории — иной, т. е., что угол поворота j в изотопич. пр-ве зависит от координат в пространстве-времени: j=j(r, t). Такой поворот на угол j(r, t) наз. калибровочным (или градиентным) преобразованием. Если законы природы не зависят от такого локального произвола в выборе суперпозиций, то в ур-ниях движения с необходимостью появляется слагаемое, учитывающее вз-ствие ч-ц. Действительно, ур-ние движения свободного нуклона, описывающее изменение волн. ф-ции со временем (см. ДИРАКА УРАВНЕНИЕ), содержит производные по времени, а следовательно (из требования релятивистской инвариантности), и по координате от волн. ф-ции (от поля). Поэтому при повороте на j(r, t) ур-ния приобретут добавку, пропорц. производной j по t и r. Эта добавка при преобразованиях Лоренца изменяется как четырёхмерный вектор (4-вектор), и, чтобы её компенсировать, в ур-ния движения следует добавить какие-то новые векторные поля, к-рые при подобных поворотах также приобретали бы добавку, пропорц. производной от j, но с обратным знаком. Таким образом, К. с. приводит к необходимости существования векторных калибровочных полей, обмен квантами к-рых обусловливает вз-ствия ч-ц.

Не обязательно, чтобы калибровочные преобразования «перепутывали» разные ч-цы (как протон и нейтрон). В квант. электродинамике ту же роль играют веществ. и мнимая части волн. ф-ции эл-на (yе), а роль изотопич. пр-ва — плоскость комплексного переменного, где по одной оси откладывается веществ. часть yе, а по другой — мнимая. Комплексную ф-цию yе можно представить в виде произведения модуля на фазовый множитель, тогда поворот в этом пр-ве на угол j сведётся к изменению фазового множителя, т. е. к умножению yе на новый фазовый множитель: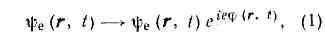

где е в показателе экспоненты — заряд эл-на. При подстановке преобразованной ф-ции в ур-ние Дирака

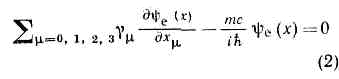(х — четырёхмерная координата с компонентами х0- ct, х1=х, х2=у, х3=z, gm— т. н. матрицы Дирака), описывающего движение свободного эл-на, появляется добавка

ieSmgm((дj(x)/дxm),

т. е. ур-ние не имеет К. с. Чтобы обеспечить К. с. и компенсировать эту добавку, необходимо изменить ур-ние (2), приписав к его правой части ieSmgmAm(x)ye(x), где поле Аm(x) при калибровочных преобразованиях переходит в Аm(x)+дj(x)/дxm. Т. о., для выполнения требования калибровочной инвариантности эл-н должен взаимодействовать с нек-рым векторным полем Аm . Если же записать ур-ния для этого поля так, чтобы они сами были калибровочно-инвариантиыми, то получаются Максвелла уравнения. Следовательно, компенсирующим (калибровочным) полем для калибровочного преобразования волн. ф-ции эл-на оказывается эл.-магн. поле, а калибровочной ч-цей — фотон, безмассовая ч-ца со спином 1. Эти два св-ва — отсутствие массы и спин 1 присущи любым калибровочным полям.

В квантовой хромодинамике, описывающей динамику кварков, вместо одного появляются три «цветных» фермиона, но все рассуждения остаются без изменения, за исключением того, что калибровочные преобразования, кроме изменения фазы, могут менять и «цвет» (т. к. при наличии полной симметрии «цвет» так же ненаблюдаем, как и фаза):

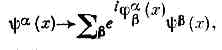где индексы a и b соответствуют трем возможным значениям «цвета» кварков. В результате вместо одной фазы появляются восемь изменяющих «цвет» фаз jab(х) (девятая соответствует общей фазе, Sajaa(x), и сохранению общего барионного заряда). Чтобы компенсировать изменение в ур-ниях движения в этом случае, приходится вводить восемь «цветных» т. н. глюонных полей (Янга — Миллса полей), квантами к-рых явл. «цветные» безмассовые глюоны. Обмен глюонами приводит к вз-ствию кварков. Поскольку в отличие от фотонов глюоны, как и кварки, оказываются «цветными» («заряженными»), они также должны взаимодействовать посредством испускания и поглощения глюонов, т. е. ур-ния для глюонного поля (в отличие от ур-ний Максвелла в вакууме) оказываются нелинейными. Калибровочные теории и калибровочные поля такого рода наз. н е а б е л е в ы м и.

Идея калибровочной инвариантности оказалась наиб. плодотворной в единой теории слабого и эл.-магн. вз-ствий (см. СЛАБОЕ ВЗАИМОДЕЙСТВИЕ). В этой теории, наряду с фотоном, осуществляющим эл.-магн. вз-ствие, появляются новые векторные бозоны— ч-цы, переносящие слабое вз-ствие. Такие промежуточные векторные бозоны должны быть массивными вследствие того, что слабое вз-ствие проявляется лишь на очень малых расстояниях, 10-15 см. Однако кванты калибровочных полей должны быть безмассовыми, появление у них массы нарушает калибровочную инвариантность ур-ний движения. Выход из этого затруднения был предложен П. Хиггсом (США, 1964) и состоит в том, что в дополнение к спинорным полям, без нарушения К. с., вводятся связанные друг с другом калибровочными преобразованиями самодействующие скалярные поля (поля X и г г с а). Самодействие этих полей выбирается так, чтобы калибровочно-инвариантное решение стало неустойчивым, т. е. не соответствующим минимуму потенц. энергии. Минимальной же энергии при этом соответствует непрерывная серия решений, каждое из к-рых не инвариантно относительно калибровочных преобразований, но серия в целом калибровочно инвариантна: при калибровочных преобразованиях одно решение переходит в другое. Нарушение симметрии состоит в том, что в природе реализуется только одно из этих решений. Это явление наз. спонтанным нарушением симметрии, или эффектом Хиггса. Оно позволяет сделать бозоны тяжёлыми без нарушения К. с. в самих ур-ниях движения. При этом оказывается, что в число промежуточных векторных бозонов входят как электрически заряженные (W+ и W-), так и нейтральный (Z°). Масса Z° должна быть =90 ГэВ, a W± =80 ГэВ; масса фотона остаётся равной нулю.

Интересной проблемой квант. теории поля явл. включение в единую калибровочную схему и сильного вз-ствия (т. н. «великое объединение»), Другим перспективным направлением объединения считается т. н. суперкалибровочная симметрия, или просто суперсимметрия. В отличие от обычных калибровочных преобразований, «перемешивающих» ч-цы с одним и тем же спином, суперкалибровочные преобразования «перемешивают» поля, кванты к-рых имеют разные спины, напр. бозоны со спином 1 и фермионы со спином 1/2, т. е. ч-цы, подчиняющиеся разным статистикам. Аналогично электродинамике такие преобразования также можно представить в виде «поворотов», но уже в нек-ром «суперкомплексном» пр-ве суперполей Ф=b+hf, где b, f — соотв. бозонное и фермионное поля, а h — нек-рая единица «фермионной части» этого пр-ва (аналог мнимой единицы i), удовлетворяющая условию hh=0. Подобные построения в принципе позволяют включить в единую схему не только сильное, но и гравитац. вз-ствие, однако известные попытки объединения всех полей на основе суперсимметрий пока не могут претендовать на описание реального мира (см. СУПЕРСИММЕТРИЯ).