Akademik

МАЯТНИК

МАЯТНИК: твёрдое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси. Обычно под М. понимают тело, совершающее колебания под действием силы тяжести; при этом ось М. не должна проходить через центр тяжести тела. Простейший М. состоит из небольшого массивного груза С, подвешенного на нити (или лёгком стержне) длиной l. Если считать нить нерастяжимой и пренебречь размерами груза по сравнению с длиной нити, а массой нити по сравнению с массой груза, то груз на нити можно рассматривать как материальную точку, находящуюся на неизменном расстоянии l от точки подвеса О (рис. 1, а). Такой М. наз. м а т е м а т и ч е с к и м. Если же колеблющееся тело нельзя рассматривать как материальную точку, то М. наз. ф и з и ч е с к и м.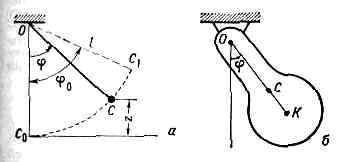

Рис. 1. Маятники: а — круговой математический; б — физический.

Математический маятник. Если М., отклонённый от равновесного положения C0, отпустить без нач. скорости или сообщить точке С скорость, направленную перпендикулярно ОС и лежащую в плоскости нач. отклонения, то М. будет совершать колебания в одной вертикальной плоскости и точка С будет двигаться по дуге окружности (плоский, или круговой математич. М.). В этом случае положение М. определяется одной координатой, напр, углом отклонения j от положения равновесия. В общем случае колебания М. не являются гармоническими; их период Т зависит от амплитуды. Если же отклонения М. малы, он совершает колебания, близкие к гармоническим, с периодом:

Т=2p?(l/g),

где g — ускорение свободного падения; в этом случае период Т не зависит от амплитуды, т. е. колебания изохронны.

Если отклонённому М. сообщить нач. скорость, не лежащую в плоскости начального отклонения, то точка С будет описывать на сфере радиуса l кривые, заключённые между двумя параллелями z=z1 и z=z2 (рис. 2, а), где значения z1 и z2 зависят от нач. условий (сферический М.). В частном случае, при z1=z2 (рис. 2, б) точка С будет описывать окружность в горизонтальной плоскости (конический М.). Интерес представляет ещё циклоидальный маятник, колебания к-рого изохронны при любой величине амплитуды.

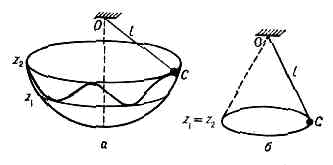Рис. 2. Маятники: а — сферический; б — конический.

Физический маятник. М. представляет собой тв. тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса (рис. 1, б). Движение такого М. вполне аналогично движению кругового математич. М. При малых углах отклонения j М. также совершает колебания, близкие к гармоническим, с периодом:

Т=2p?(I/Mgl),

где I — момент инерции М. относительно оси подвеса, l — расстояние от оси подвеса О до центра тяжести С, М — масса М. Следовательно, период колебаний физ. М. совпадает с периодом колебаний такого математич. М., к-рый имеет длину l0=I/Мl. Эта длина наз. приведённой длиной данного физ. М.

Точка К на продолжении прямой ОС, находящаяся на расстоянии l0 от оси подвеса, наз. центром качаний физ. М. При этом расстояние ОK=l0 всегда больше, чем ОС=l, Точка О оси подвеса М. и центр качания обладают св-вом взаимности; если ось подвеса сделать проходящей через центр качаний, то точка О прежней оси подвеса станет новым центром качаний и период колебаний М. не изменится. Это св-во взаимности используется в оборотном маятнике для определения приведённой длины l0; зная l0 и Т, можно найти значение g в данном месте.

Св-вами М. широко пользуются в разл. приборах: в часах, в приборах для определения ускорения силы тяжести, ускорений движущихся тел, колебаний земной коры, в гироскопич. устройствах, в приборах для эксперим. определения момента инерции тел и др. (см. ФУКО МАЯТНИК).

МАЯТНИК

- твёрдое тело, совершающее под действием приложенных сил колебания около неподвижной точки или оси. В физике под M. обычно понимают разл. колебат. систем с симметрией эллипса. Введены Э. Матьё (E. Mathieu) в 1868.

Единого определения и единых обозначений для M. ф. не существует. Обычно под M. ф. (1-го рода) понимают периодические (с периодом 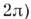решения ур-ния (1), удовлетворяющие граничным условиям

[нечётные M. ф., обозначаемы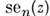е , где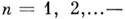

число нулей на интервале 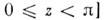или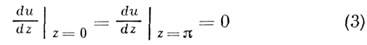

[чётные M. ф., обозначаемые 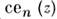, где n =0, 1, 2,...-

число нулей на интервале 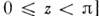. При 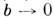эти ф-ции сводятся к тригонометрическим.

M. ф. существуют лишь в том случае, когда точка (а, b) в пространстве параметров ур-ния (1) лежит на границе зоны устойчивости, внутри к-рой решения ур-ния (1) ограничены. Граничные условия (2) и (3) определяют M. ф. с точностью до множителя, к-рый можно задать, выбрав надлежащие условия нормировки, напр.

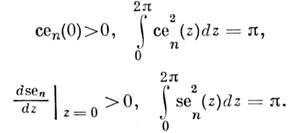
Менее распространены M. ф. 2-го рода - непериодические решения ур-ния (1), обозначаемые 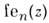и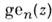

M. ф. можно получить и как решения интегрального ур-ния; они удовлетворяют соотношениям ортогональности, вытекающим из ур-ния (1) и граничных условий (2) и (3):

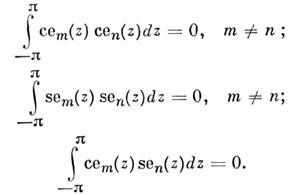
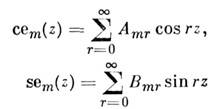
M. ф. допускают разложение в ряды Фурье (суммирование по чётным rдля чётных т и по нечётным rдля нечётных т), а также в ряды по ф-циям Бесселя и произведениям ф-ций Бесселя.

Модифицированные M. ф. (1-го рода) определены как

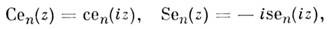
они удовлетворяют ур-нию, к-рое получается из ур-ния (1) при замене 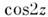на 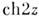(модифициров. ур-ние Матьё).

Лит.: Уиттекер Э. Т., Ватсон Д. H., Курс современного анализа, пер. с англ., ч. 2, 2 изд., M., 1963; Mак -Лахлан H. В., Теория и приложения функций Матьё, пер. с англ., M., 1953; Бейтмен Г., Эрдейи А., Высшие трансцендентные функции, пер. с англ., [т. 3], M., 1967.

Ю. А. Данилов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.