- КОЛЕБАНИЯ
-
движения или процессы, обладающие той или иной степенью повторяемости во времени. К. свойственны всем явлениям природы: пульсирует излучение звёзд, внутри к-рых происходят циклич. яд. реакции; с высокой степенью периодичности вращаются планеты Солн. системы; движение Луны вызывает приливы и отливы на Земле; в земной ионосфере и атмосфере циркулируют потоки заряж. и нейтр. ч-ц; ветры возбуждают К. и волны на поверхности водоёмов и т. д. Внутри любого живого организма непрерывно происходят разнообразные, ритмично повторяющиеся процессы, напр. с удивительной надёжностью бьётся человеческое сердце, даже психика людей подвержена К. В виде сложнейшей совокупности К. ч-ц и полей (эл-нов, фотонов, протонов и др.) можно представить «устройство» микромира.В технике К. либо выполняют определённые функцией, обязанности (маятник, колебат. контур, генератор К. и др.), либо возникают как неизбежное проявление физ. св-в (вибрации машин и сооружений, неустойчивости и вихревые потоки при движении тел в газах и т. д.).В физике выделяются К. механические, электромагнитные и их комбинации. Это обусловлено той исключит. ролью, к-рую играют гравитац. и эл.-магн. вз-ствия в масштабах, характерных для жизнедеятельности человека. С помощью распространяющихся механич. К. плотности и давления воздуха, воспринимаемых нами как звук, а также очень быстрых К. электрич. и магн. полей, воспринимаемых нами как свет, мы получаем б. ч. прямой информации об окружающем мире.К. любых физ. величин почти всегда связаны с попеременным превращением энергии одного вида в энергию другого вида. Так, при отклонении маятника (груза на нити, рис. 1) от положения равновесия увеличивается потенц. энергия груза, запасённая им в поле тяжести; если груз отпустить, он падает, вращаясь около точки подвеса как около центра; в крайнем нижнем положении потенц. энергия превращается в кинетическую, и груз проскакивает это равновесное положение, увеличивая снова потенц. энергию. Далее процесс перекачки энергии повторяется, пока рассеяние (диссипация) энергии, обусловленное, напр., трением, не приводит к полному прекращению К.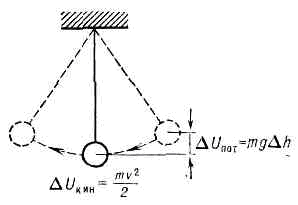 Рис. 1. Схема колебаний маятника: m — масса груза; g — ускорение силы тяжести; Dh — высота подъёма груза; v — его макс. скорость.В случае К. электрич. зарядов и токов в колебательном контуре или электрич. и магн. полей в эл.-магн. волнах роль потенциальной играет электрическая энергия, а кинетической — магнитная.По мере изучения К. разл. физ. природы возникло убеждение о возможности общего, «внепредметного», подхода к ним, основанного на св-вах и закономерностях колебат. процессов вообще. В результате появилась теория К. и волн. Осн. матем. аппаратом теории К. первоначально служили дифф. ур-ния в обыкновенных производных. Однако со временем изучаемые ею модели по существу распространились на все виды описаний динамич. систем: от интегродифференциально разностных до статистических (подробнее (см. КОЛЕБАНИЙ И ВОЛН ТЕОРИЯ)).Кинематика К. позволяет выделить несколько наиб. типичных примеров (рис. 2). Для простоты будем говорить о К., описываемых ф-цией времени u(t), хотя с кинематич. точки зрения пространств. и временные К. взаимно сводятся друг к другу путём перехода из одной системы отсчёта к другой.
Рис. 1. Схема колебаний маятника: m — масса груза; g — ускорение силы тяжести; Dh — высота подъёма груза; v — его макс. скорость.В случае К. электрич. зарядов и токов в колебательном контуре или электрич. и магн. полей в эл.-магн. волнах роль потенциальной играет электрическая энергия, а кинетической — магнитная.По мере изучения К. разл. физ. природы возникло убеждение о возможности общего, «внепредметного», подхода к ним, основанного на св-вах и закономерностях колебат. процессов вообще. В результате появилась теория К. и волн. Осн. матем. аппаратом теории К. первоначально служили дифф. ур-ния в обыкновенных производных. Однако со временем изучаемые ею модели по существу распространились на все виды описаний динамич. систем: от интегродифференциально разностных до статистических (подробнее (см. КОЛЕБАНИЙ И ВОЛН ТЕОРИЯ)).Кинематика К. позволяет выделить несколько наиб. типичных примеров (рис. 2). Для простоты будем говорить о К., описываемых ф-цией времени u(t), хотя с кинематич. точки зрения пространств. и временные К. взаимно сводятся друг к другу путём перехода из одной системы отсчёта к другой.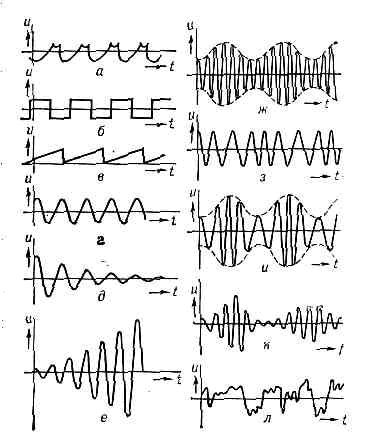 Рис. 2. Разл. виды колебаний: а — периодич. колебания сложной формы; б — прямоуг. колебания; в — пилообразные; г — синусоидальные; д — затухающие; е — нарастающие; ж — амплитудно-модулированные; в — частотно-модулированные; и — колебания, модулированные по амплитуде и по фазе; к — колебания, амплитуда и фаза к-рых — случайные ф-ции; л — случайные колебания; u — колеблющаяся величина; t — время.На рис. 2, а— г показаны периодич. К. разл. формы, в к-рых любое значение u(t) повторяется через одинаковые промежутки времени Т, наз. периодом К., т. е. u(t+T)=u(t). Величину, обратную периоду Т и равную числу К. в ед. времени, наз. частотой К. n=1/T; пользуются также круговой или циклич. частотой w=2pn. В случае пространств. К. вводят аналогичные понятия пространств. периода (или длины волны Я) и волн. числа k=2p/l.Разновидностями периодич. К. явл. прямоугольные (рис. 2, б), пилообразные (рис. 2, в) и наиб. важные синусоидальные, или гармонические колебания (рис. 2, г). Последние могут быть записаны в виде:u(t)=asinj=asin(wt+j0),где а — амплитуда, j — фаза, j0 — её нач. значение. В случае строго гармонич. К. величины а, w и j0 не зависят от времени. Часто употребляется также комплексная запись синусоидальных К.
Рис. 2. Разл. виды колебаний: а — периодич. колебания сложной формы; б — прямоуг. колебания; в — пилообразные; г — синусоидальные; д — затухающие; е — нарастающие; ж — амплитудно-модулированные; в — частотно-модулированные; и — колебания, модулированные по амплитуде и по фазе; к — колебания, амплитуда и фаза к-рых — случайные ф-ции; л — случайные колебания; u — колеблющаяся величина; t — время.На рис. 2, а— г показаны периодич. К. разл. формы, в к-рых любое значение u(t) повторяется через одинаковые промежутки времени Т, наз. периодом К., т. е. u(t+T)=u(t). Величину, обратную периоду Т и равную числу К. в ед. времени, наз. частотой К. n=1/T; пользуются также круговой или циклич. частотой w=2pn. В случае пространств. К. вводят аналогичные понятия пространств. периода (или длины волны Я) и волн. числа k=2p/l.Разновидностями периодич. К. явл. прямоугольные (рис. 2, б), пилообразные (рис. 2, в) и наиб. важные синусоидальные, или гармонические колебания (рис. 2, г). Последние могут быть записаны в виде:u(t)=asinj=asin(wt+j0),где а — амплитуда, j — фаза, j0 — её нач. значение. В случае строго гармонич. К. величины а, w и j0 не зависят от времени. Часто употребляется также комплексная запись синусоидальных К.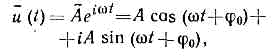 к-рая удобна при расчётах, однако физ. смысл имеют отдельно вещественная и мнимая части. При этом комплексная амплитуда А»Аеij0 объединяет в себе действит. значения амплитуды и фазы К. Для показанного на рис. 2, д затухающего К.
к-рая удобна при расчётах, однако физ. смысл имеют отдельно вещественная и мнимая части. При этом комплексная амплитуда А»Аеij0 объединяет в себе действит. значения амплитуды и фазы К. Для показанного на рис. 2, д затухающего К.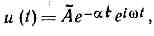 где коэфф. затухания а можно относить либо к мнимой части комплексной частоты w»w+ia, либо к экспоненциально убывающей амплитуде. Иногда вводят понятие декремента затухания d=aТ; при отрицательных б этот коэфф. наз. инкрементом, амплитуда соответствующего К. экспоненциально нарастает. У К. с перем. амплитудой периодичность нарушается; но при a-w их всё же можно считать почти (квази) периодическими, а при a->w — почти апериодическими, т. е. по существу уже не К., а монотонными процессами. Для передачи информации применяются модулиров. К. (рис. 2, ж—и), амплитуда, фаза или частота к-рых изменяются по определ. закону в соответствии с передаваемыми сигналами, напр. в радиовещании ВЧ К. модулируются К. звук. частот, передающими речь, музыку (см. МОДУЛЯЦИЯ КОЛЕБАНИЙ).При изучении стохастич. процессов приходится иметь дело с частично и полностью случайными К. На рис. 2, к показан пример синусоидального К., модулированного по амплитуде и фазе случайными ф-циями, а на рис. 2, л дана одна из реализаций совершенно неупорядоченного процесса («белого шума»), к-рый лишь условно можно отнести к К.Колебат. движения на плоскости и в пр-ве в принципе могут быть представлены как совокупность одномерных К. вдоль соответствующих осей координат. Так, два гармонич. К. (одномерные осцилляторы) с частотами nw (вдоль оси х) и mw (вдоль оси у^х) (при рациональном отношении п/т) явл. проекциями сложных периодических плоских К., наз. Лиссажу фигурами. Равномерное движение по окружности (ротатор) можно разложить на два одинаковых гармонич. К. (n=m), сдвинутых по фазе на p/2. В природе и во мн. техн. устройствах часто возникают движения, почти не отличающиеся (на протяжении больших промежутков времени) от чисто гармонических или равномерно вращательных. Мн. физ. приборы (спектр. анализаторы) выделяют из произвольных процессов наборы К., близких к гармоническим. Возможна и обратная процедура синтеза гармонич. К., математически соответствующая рядам и интегралам Фурье, в силу к-рой любой временной процесс можно воссоздать сложением или интегрированием гармонич. К. разл. частот и амплитуд.Динамика К. Свободные, или собственные, К. явл. движением системы, предоставленной самой себе, в отсутствии внеш. воздействий. При малых отклонениях от состояния равновесия движения системы удовлетворяют суперпозиции принципу, согласно к-рому сумма двух произвольных движений также составляет допустимое движение системы; такие движения описываются линейными ур-ниями (в частности, дифференциальными). Если система ещё и консервативна (т. е. в ней нет потерь или притока энергии извне), а её параметры не изменяются во времени (о переменных параметрах будет сказано ниже), то любое собств. К. может быть однозначно представлено как сумма нормальных колебаний, синусоидально изменяющихся во времени с определёнными собств. частотами. В колебат. системах с сосредоточенными параметрами, состоящих из N связанных осцилляторов (напр., цепочка из колебат. электрич. контуров или из соединённых упругими пружинками шариков), число норм. колебаний (мод) равно N. В системах с распределёнными параметрами (струна, мембрана, полый или открытый резонатор) таких К. существует бесконечное множество. Напр., для струны длиной L с закреплёнными концами моды отличаются числом полуволн, к-рые можно уложить на всей длине струны: L=nl/2(n=0, 1, 2, . . ., ?). Если скорость распространения волн вдоль струны равна v, то спектр собств. частот определяется ф-лой: wn=knv=2p/Tn=2pv/ln=npv/L (n=0, 1, 2, . . ., ?). Наличие дисперсии, когда v=v(w), искажает это простое эквидистантное распределение частот, спектр к-рых определяется уже из т. н. дисперсионного ур-ния: wn=w(kn)=(np/L)v(wn). В реальных системах собств. К. будут затухать из-за потерь, поэтому их можно считать приближённо гармоническими лишь в интервале времени, меньшем 1/a. Затухающее К. (рис. 2, д) можно представить в виде пакета гармонич. К., непрерывно заполняющих интервал частот (w0:±Dw), тем более узкого, чем меньше a, т. к. Dw=a. В этом случае говорят об уширении спектр. линии. Т. о., сгущение спектра из-за дисперсии и уширение линии из-за потерь может повлечь за собой превращение дискр. спектра в сплошной (ширина линий становится прибл. равной интервалу между ними, т. е Dw=a=(wn+1-wn).Наличие даже слабой нелинейности систем с дискр. спектром собств. частот приводит к «перекачке» энергии К. по спектр. компонентам; при этом возникают процессы «конкуренции мод» — выживание одних и подавление других. Дисперсия может стабилизировать эти процессы и привести к формированию устойчивых пространственно-временных образований, примерами к-рых в системах с непрерывным спектром явл. солитоны.Возбуждение К. происходит: либо путём непосредств. воздействия на колебат. систему (раскачка маятника периодич. толчками, включение периодической эдс в колебат. контур и т. д.) — в этом случае говорят о вынужденных колебаниях; либо путём периодич. изменения параметров колебат. системы (длины подвеса маятника, ёмкости или самоиндукции контура, коэфф. упругости струны и т. п.) — т. н. параметрич. возбуждение колебаний; либо благодаря развитию неустойчивостей и возникновению самосогласованных колебат. движений внутри самой системы — т. н. автоколебания.Особое значение при возбуждении К. имеет явление резонанса, состоящее в резком увеличении амплитуды К. при приближении частоты внеш. воздействия к нек-рой резонансной частоте, характеризующей систему. Если последняя линейна и параметры её не зависят от времени, то резонансные частоты совпадают с частотами её собств. К. и соответствующий отклик тем сильнее, чем выше добротность К. Раскачка происходит до тех пор, пока энергия, вносимая извне (напр., при каждом отклонении маятника), превышает потери за период осцилляции. Для линейных К. энергия, получаемая от источника, пропорц. первой степени амплитуды, а потери растут пропорц. её квадрату, поэтому баланс энергий всегда достижим.При больших амплитудах К. становятся нелинейными, происходит смещение собств. частот системы и обогащение их спектра гармониками и субгармониками. Ограничение амплитуды колебаний может быть обусловлено как нелинейной диссипацией энергии, так и уходом системы из резонанса. При возбуждении К. в системах с распределёнными параметрами макс. амплитуды достигаются в случае пространственно-временного резонанса, когда не только частота внеш. воздействия, но и его распределение по координатам хорошо «подогнаны» к структуре норм. моды или, на языке бегущих волн, когда наступает совмещение не только их частот (резонанс), но и волн. векторов (синхронизм) .Существует нек-рый выделенный класс вынужденных К., при к-ром внеш. воздействие, не являясь чисто колебательным (напр., мгновенный удар), имеет, однако, настолько богатый частотный спектр, что в нём всегда содержатся резонансные частоты системы. Напр., заряж. ч-ца, пролетающая между двумя металлич. плоскостями, возбуждает почти весь набор нормальных эл.-магн. К. и волн, свойственный этой системе. Сюда же следует отнести черенковское излучение (см. ЧЕРЕНКОВА — ВАВИЛОВА ИЗЛУЧЕНИЕ) или тормозное излучение ч-цы в однородных средах, когда и спектр внеш. воздействия и спектр собственных К.— оба сплошные, т. е. в них представлены все возможные частоты. Наконец, есть и совсем аномальный случай вынужденных К. в системах с непрерывным спектром собств. частот типа ротатора (маховик, колесо, эл-н в магн. поле и т. п.), где вращат. движение (а следовательно, и два ортогональных колебат. движения) может возбуждаться силами, неизменными во времени.Параметрич. возбуждение К. возникает при периодич. воздействии на те параметры системы, к-рые определяют величину запасённой колебат. энергии: в электрич. контуре — это индуктивность или ёмкость (но не сопротивление), у маятника — это длина нити или масса груза (но не коэфф. трения). (см. ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС, ПАРАМЕТРИЧЕСКАЯ ГЕНЕРАЦИЯ И УСИЛЕНИЕ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ).При определ. условиях в такой нелинейной колебат. системе могут возникать непрекращающиеся самоподдерживающиеся К., или автоколебания, при к-рых внеш. источнику отводится лишь ф-ция восполнения потерь энергии на диссипацию. Процесс формирования автоколебаний обычно состоит в последовательном самосогласовании движений. Пусть нач. состояние системы неустойчиво либо по отношению к ничтожно малым флуктуациям (мягкий режим возбуждения), либо по отношению к определ. конечным возмущениям (жёсткий режим возбуждения). В любом случае спонтанно (случайно) возникшее К. начнёт увеличиваться по амплитуде (процесс усиления К.), эти усиленные К. через элемент положительной обратной связи, обеспечивающий самосогласованность фаз, снова «подаются» в место своего возникновения и снова усиливаются и т. д. Получается очень быстрый (чаще всего экспоненциальный) рост К. Ограничение К. наступает из-за конечности энергетич. ресурсов, а также из-за рассогласованности фаз (подробнее (см. АВТОКОЛЕБАНИЯ)).К. могут быть самого широкого диапазона частот v и периодов Т. Так, приведём для примера значения Т или v для нек-рых важнейших К. и вращений: теор. модель пульсации Вселенной (T=1017—1018 с); обращение Солнца вокруг центра Галактики (T=1016 с); ледниковые периоды на Земле (7'=1011—1012 с); наибольший цикл солн. активности (T=7•108 с); обращение Земли вокруг Солнца — год (T=3•107 с); обращение Луны вокруг Земли — лунный месяц (Т=2,4•106 с); вращение Земли вокруг своей оси — сутки (T=9•104 с); оборот часовой стрелки (T=4,3•104 с); оборот минутной стрелки (T=36•103с); ветровые волны на море (Т=1 с или n=l Гц); опасные для человека инфразвуки (n=5—10 Гц); колесо автомобиля при скорости 60 км/ч (n=10 Гц); звук. волны, воспринимаемые человеком на слух (n=20—2•104 Гц); стандартная частота К. перем. тока (n=50 Гц); УЗ (n=2•104—109 Гц); эл.-магнитного К. радиодиапазона (n=105—3•108 Гц); эл.-магн. К. СВЧ диапазона (n=3•108—3•1011); гиперзвук (n=109—1013 Гц); типичные колебания атомов в молекуле (n=1011—1013 Гц); оптика (видимый свет) (n=0,4•1014—0,75•1014 Гц); УФ излучение (n=1015—1017 Гц); рентг. изяучение (n=1018—1019 Гц); гамма-лучи (n=1020 Гц); короткоживущие частицы — резонансы (T=10-22—10-24 с).
где коэфф. затухания а можно относить либо к мнимой части комплексной частоты w»w+ia, либо к экспоненциально убывающей амплитуде. Иногда вводят понятие декремента затухания d=aТ; при отрицательных б этот коэфф. наз. инкрементом, амплитуда соответствующего К. экспоненциально нарастает. У К. с перем. амплитудой периодичность нарушается; но при a-w их всё же можно считать почти (квази) периодическими, а при a->w — почти апериодическими, т. е. по существу уже не К., а монотонными процессами. Для передачи информации применяются модулиров. К. (рис. 2, ж—и), амплитуда, фаза или частота к-рых изменяются по определ. закону в соответствии с передаваемыми сигналами, напр. в радиовещании ВЧ К. модулируются К. звук. частот, передающими речь, музыку (см. МОДУЛЯЦИЯ КОЛЕБАНИЙ).При изучении стохастич. процессов приходится иметь дело с частично и полностью случайными К. На рис. 2, к показан пример синусоидального К., модулированного по амплитуде и фазе случайными ф-циями, а на рис. 2, л дана одна из реализаций совершенно неупорядоченного процесса («белого шума»), к-рый лишь условно можно отнести к К.Колебат. движения на плоскости и в пр-ве в принципе могут быть представлены как совокупность одномерных К. вдоль соответствующих осей координат. Так, два гармонич. К. (одномерные осцилляторы) с частотами nw (вдоль оси х) и mw (вдоль оси у^х) (при рациональном отношении п/т) явл. проекциями сложных периодических плоских К., наз. Лиссажу фигурами. Равномерное движение по окружности (ротатор) можно разложить на два одинаковых гармонич. К. (n=m), сдвинутых по фазе на p/2. В природе и во мн. техн. устройствах часто возникают движения, почти не отличающиеся (на протяжении больших промежутков времени) от чисто гармонических или равномерно вращательных. Мн. физ. приборы (спектр. анализаторы) выделяют из произвольных процессов наборы К., близких к гармоническим. Возможна и обратная процедура синтеза гармонич. К., математически соответствующая рядам и интегралам Фурье, в силу к-рой любой временной процесс можно воссоздать сложением или интегрированием гармонич. К. разл. частот и амплитуд.Динамика К. Свободные, или собственные, К. явл. движением системы, предоставленной самой себе, в отсутствии внеш. воздействий. При малых отклонениях от состояния равновесия движения системы удовлетворяют суперпозиции принципу, согласно к-рому сумма двух произвольных движений также составляет допустимое движение системы; такие движения описываются линейными ур-ниями (в частности, дифференциальными). Если система ещё и консервативна (т. е. в ней нет потерь или притока энергии извне), а её параметры не изменяются во времени (о переменных параметрах будет сказано ниже), то любое собств. К. может быть однозначно представлено как сумма нормальных колебаний, синусоидально изменяющихся во времени с определёнными собств. частотами. В колебат. системах с сосредоточенными параметрами, состоящих из N связанных осцилляторов (напр., цепочка из колебат. электрич. контуров или из соединённых упругими пружинками шариков), число норм. колебаний (мод) равно N. В системах с распределёнными параметрами (струна, мембрана, полый или открытый резонатор) таких К. существует бесконечное множество. Напр., для струны длиной L с закреплёнными концами моды отличаются числом полуволн, к-рые можно уложить на всей длине струны: L=nl/2(n=0, 1, 2, . . ., ?). Если скорость распространения волн вдоль струны равна v, то спектр собств. частот определяется ф-лой: wn=knv=2p/Tn=2pv/ln=npv/L (n=0, 1, 2, . . ., ?). Наличие дисперсии, когда v=v(w), искажает это простое эквидистантное распределение частот, спектр к-рых определяется уже из т. н. дисперсионного ур-ния: wn=w(kn)=(np/L)v(wn). В реальных системах собств. К. будут затухать из-за потерь, поэтому их можно считать приближённо гармоническими лишь в интервале времени, меньшем 1/a. Затухающее К. (рис. 2, д) можно представить в виде пакета гармонич. К., непрерывно заполняющих интервал частот (w0:±Dw), тем более узкого, чем меньше a, т. к. Dw=a. В этом случае говорят об уширении спектр. линии. Т. о., сгущение спектра из-за дисперсии и уширение линии из-за потерь может повлечь за собой превращение дискр. спектра в сплошной (ширина линий становится прибл. равной интервалу между ними, т. е Dw=a=(wn+1-wn).Наличие даже слабой нелинейности систем с дискр. спектром собств. частот приводит к «перекачке» энергии К. по спектр. компонентам; при этом возникают процессы «конкуренции мод» — выживание одних и подавление других. Дисперсия может стабилизировать эти процессы и привести к формированию устойчивых пространственно-временных образований, примерами к-рых в системах с непрерывным спектром явл. солитоны.Возбуждение К. происходит: либо путём непосредств. воздействия на колебат. систему (раскачка маятника периодич. толчками, включение периодической эдс в колебат. контур и т. д.) — в этом случае говорят о вынужденных колебаниях; либо путём периодич. изменения параметров колебат. системы (длины подвеса маятника, ёмкости или самоиндукции контура, коэфф. упругости струны и т. п.) — т. н. параметрич. возбуждение колебаний; либо благодаря развитию неустойчивостей и возникновению самосогласованных колебат. движений внутри самой системы — т. н. автоколебания.Особое значение при возбуждении К. имеет явление резонанса, состоящее в резком увеличении амплитуды К. при приближении частоты внеш. воздействия к нек-рой резонансной частоте, характеризующей систему. Если последняя линейна и параметры её не зависят от времени, то резонансные частоты совпадают с частотами её собств. К. и соответствующий отклик тем сильнее, чем выше добротность К. Раскачка происходит до тех пор, пока энергия, вносимая извне (напр., при каждом отклонении маятника), превышает потери за период осцилляции. Для линейных К. энергия, получаемая от источника, пропорц. первой степени амплитуды, а потери растут пропорц. её квадрату, поэтому баланс энергий всегда достижим.При больших амплитудах К. становятся нелинейными, происходит смещение собств. частот системы и обогащение их спектра гармониками и субгармониками. Ограничение амплитуды колебаний может быть обусловлено как нелинейной диссипацией энергии, так и уходом системы из резонанса. При возбуждении К. в системах с распределёнными параметрами макс. амплитуды достигаются в случае пространственно-временного резонанса, когда не только частота внеш. воздействия, но и его распределение по координатам хорошо «подогнаны» к структуре норм. моды или, на языке бегущих волн, когда наступает совмещение не только их частот (резонанс), но и волн. векторов (синхронизм) .Существует нек-рый выделенный класс вынужденных К., при к-ром внеш. воздействие, не являясь чисто колебательным (напр., мгновенный удар), имеет, однако, настолько богатый частотный спектр, что в нём всегда содержатся резонансные частоты системы. Напр., заряж. ч-ца, пролетающая между двумя металлич. плоскостями, возбуждает почти весь набор нормальных эл.-магн. К. и волн, свойственный этой системе. Сюда же следует отнести черенковское излучение (см. ЧЕРЕНКОВА — ВАВИЛОВА ИЗЛУЧЕНИЕ) или тормозное излучение ч-цы в однородных средах, когда и спектр внеш. воздействия и спектр собственных К.— оба сплошные, т. е. в них представлены все возможные частоты. Наконец, есть и совсем аномальный случай вынужденных К. в системах с непрерывным спектром собств. частот типа ротатора (маховик, колесо, эл-н в магн. поле и т. п.), где вращат. движение (а следовательно, и два ортогональных колебат. движения) может возбуждаться силами, неизменными во времени.Параметрич. возбуждение К. возникает при периодич. воздействии на те параметры системы, к-рые определяют величину запасённой колебат. энергии: в электрич. контуре — это индуктивность или ёмкость (но не сопротивление), у маятника — это длина нити или масса груза (но не коэфф. трения). (см. ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС, ПАРАМЕТРИЧЕСКАЯ ГЕНЕРАЦИЯ И УСИЛЕНИЕ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ).При определ. условиях в такой нелинейной колебат. системе могут возникать непрекращающиеся самоподдерживающиеся К., или автоколебания, при к-рых внеш. источнику отводится лишь ф-ция восполнения потерь энергии на диссипацию. Процесс формирования автоколебаний обычно состоит в последовательном самосогласовании движений. Пусть нач. состояние системы неустойчиво либо по отношению к ничтожно малым флуктуациям (мягкий режим возбуждения), либо по отношению к определ. конечным возмущениям (жёсткий режим возбуждения). В любом случае спонтанно (случайно) возникшее К. начнёт увеличиваться по амплитуде (процесс усиления К.), эти усиленные К. через элемент положительной обратной связи, обеспечивающий самосогласованность фаз, снова «подаются» в место своего возникновения и снова усиливаются и т. д. Получается очень быстрый (чаще всего экспоненциальный) рост К. Ограничение К. наступает из-за конечности энергетич. ресурсов, а также из-за рассогласованности фаз (подробнее (см. АВТОКОЛЕБАНИЯ)).К. могут быть самого широкого диапазона частот v и периодов Т. Так, приведём для примера значения Т или v для нек-рых важнейших К. и вращений: теор. модель пульсации Вселенной (T=1017—1018 с); обращение Солнца вокруг центра Галактики (T=1016 с); ледниковые периоды на Земле (7'=1011—1012 с); наибольший цикл солн. активности (T=7•108 с); обращение Земли вокруг Солнца — год (T=3•107 с); обращение Луны вокруг Земли — лунный месяц (Т=2,4•106 с); вращение Земли вокруг своей оси — сутки (T=9•104 с); оборот часовой стрелки (T=4,3•104 с); оборот минутной стрелки (T=36•103с); ветровые волны на море (Т=1 с или n=l Гц); опасные для человека инфразвуки (n=5—10 Гц); колесо автомобиля при скорости 60 км/ч (n=10 Гц); звук. волны, воспринимаемые человеком на слух (n=20—2•104 Гц); стандартная частота К. перем. тока (n=50 Гц); УЗ (n=2•104—109 Гц); эл.-магнитного К. радиодиапазона (n=105—3•108 Гц); эл.-магн. К. СВЧ диапазона (n=3•108—3•1011); гиперзвук (n=109—1013 Гц); типичные колебания атомов в молекуле (n=1011—1013 Гц); оптика (видимый свет) (n=0,4•1014—0,75•1014 Гц); УФ излучение (n=1015—1017 Гц); рентг. изяучение (n=1018—1019 Гц); гамма-лучи (n=1020 Гц); короткоживущие частицы — резонансы (T=10-22—10-24 с).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- КОЛЕБАНИЯ
-
- движения или состояния, обладающие той или иной степенью повторяемости во времени. К. свойственны всем явлениям природы: пульсирует излучение звёзд, внутри к-рых происходят циклич. ядерные реакции; с высокой степенью периодичности вращаются планеты Солнечной системы (а всякое вращение можно представить себе как два одновременных К. во взаимно перпендикулярных направлениях); движение Луны вызывает приливы и отливы на Земле; в земной ионосфере и атмосфере циркулируют потоки заряж. и нейтральных частиц; ветры возбуждают К. и волны на поверхностях водоёмов и т. д. Внутри любого живого организма - от одиночной клетки до высокоорганизованных их популяций - непрерывно происходят разнообразные, ритмично повторяющиеся процессы (биение сердца, колебания психич. состояний и др.). В виде сложнейшей совокупности К. частиц и полей (электронов, фотонов, протонов и др.) можно представить "устройство" микромира.
В технике К. выполняют либо определ. функциональные обязанности (колесо, маятник, колебат. кои-тур, генератор К. и т. д.), либо возникают как неизбежное проявление физ. свойств (вибрации машин и сооружений, неустойчивости и вихревые потоки при движении тел в газах и т. д.).
В физике особо выделяются колебания двух видов - механич. и электромагнитные и их эл.-механич. комбинации. Это обусловлено той исключит. ролью, к-рую играют гравитац. и эл.-магн. взаимодействия в масштабах, характерных для жизнедеятельности человека. С помощью распространяющихся механич. К. плотности и давления воздуха, воспринимаемых нами как звук, а также очень быстрых колебаний электрич. и магн. полей, воспринимаемых нами как свет, мы получаем большую часть прямой информации об окружающем мире.
К. любых физ. величин почти всегда сопровождаются попеременным превращением энергии одного вида в энергию другого вида. Так, оттягивая маятник (груз на нити) от положения равновесия, мы увеличиваем потенц. энергию груза, запасённую в поле тяжести; при отпускании он начинает падать, вращаясь около точки подвеса как около центра, и в крайнем ниж. положении вся потенц. энергия превращается в кинетическую, поэтому груз проскакивает это равновесное положение, и процесс перекачки энергии повторяется, пока рассеяние (диссипация) энергии, обусловленное, напр., трением, не приведёт к полному прекращению К. В случае К. электрич. зарядов и токов в колебательном контуре или электрич. и магн. полей в эл.-магн. волнах роль потенциальной обычно играет электрич. энергия, а кинетической - магнитная. Иногда, когда речь идёт о К. тепловых, хим. и особенно информац. величин, такой энергетич. подход несколько условен, но вполне плодотворен.
Теория колебаний и волн. Изучение К. на разных этапах играло стимулирующую роль в развитии науки. Так, исследования К. маятника дали возможность Г. Галилею (G. Galilei) более точно измерять промежутки времени (1636), изучение законов обращения планет вокруг Солнца привело И. Ньютона (I. Newton) к созданию начал классич. механики (1686). Дж. К. Максвелл (J. С. Maxwell), следуя М. Фарадею (М. Faraday) и связав свойства электрич. К. с волновыми характеристиками света, построил основы классич. электродинамики (1864). В результате корпускулярноволнового рассмотрения материи появилась квантовая механика,
По мере изучения К. разл. физ. природы возникло убеждение о возможности общего, "внепредметного", подхода к ним, основанного на свойствах и закономерностях колебат. процессов вообще. В результате появилась теория К. и волн, к-рая, основываясь на матем. и физ. моделях, устанавливает общие свойства колебат. и волновых процессов в реальных системах, не интересуясь деталями их поведения, обусловленного их природой (физической, химической и др.), и определяет связь между параметрами системы и её колебат. (волновыми) характеристиками. Благодаря общности закономерностей результаты, полученные при исследовании К. и волн, напр. в механике, могут быть перенесены в оптику или радиотехнику.
Так, при создании параметрич. генераторов света были использованы данные, накопленные при анализе параметрич. К. в радиотехнике. Изучение любого волнового или колебат. процесса в каждом конкретном случае начинается с идеализации реальной системы, т е. с построения модели и написания для неё соответствующих ур-ний (дифференциальных, в частных производных, дифференциально-разностных и др.). Идеализации одних и тех же систем могут быть различными в зависимости от того, какое явление исследуется. Справедливость принятых идеализации оценивается путём сравнения результатов теории, построенной на основании данной модели, с результатами анализа более общей модели или с поведением реальной системы - экспериментом. Напр., когда речь идёт только о нахождении условий раскачки качелей при периодич. изменении их длины, модель может быть совсем простой - линейный осциллятор с периодически меняющейся собственной частотой. Когда же необходимо ответить на вопрос об амплитуде установившихся К. таких качелей, нужно уже учитывать нелинейность (зависимость частоты К. качелей от амплитуды К.), в результате чего приходим к модели физ. маятника, т. е. нелинейного осциллятора с периодически изменяемым параметром.
Понятия и представления теории К. и волн относятся либо к явлениям (резонанс, автоколебания, синхронизация, самофокусировка и т. д.), либо к моделям (линейная и нелинейная системы, система с сосредоточенными параметрами или система с распределёнными параметрами, система с одной или неск. степенями свободы и др.). На основе сложившихся представлений теории К. можно связать те или иные явления в конкретной системе с её характеристиками, фактически не решая задачи всякий раз заново. Напр., преобразование энергии одних К. в другие в слабонелинейной системе (будь то волны на воде, эл.-магн. К. в ионосфере или К. маятника на пружинке) возможно только в случае, когда выполнены определ. резонансные условия между собств. частотами подсистемы.
Методы теории К. и волн - это методы анализа ур-ний, описывающих модели реальных систем. Поэтому большинство из них являются общими с методами качеств. теории дифференц. ур-ний (метод фазового пространства, метод отображений Пуанкаре и др.), асимптотич. методами решения дифференц. и иных ур-ний (метод Ван дер Поля, метод усреднения и т. д.). Специфика методов теории К. и волн состоит в том, что при изучении моделей колебат. или волновых явлений интересуются, как правило, общими свойствами решений соответствующих ур-ний.
Осн. разделы теории К. и волн - теория устойчивости линеаризованных систем, теория параметрич. систем и адиабатич. инвариантов, теория автоколебательных и автоволновых процессов, теория ударных волн и солитонов, кинетика К. и волн в системах с большим числом степеней свободы, теория стохастич. систем - систем со сложной динамикой. Если "классич." теория К. и волн имела дело в основном с детерминированными системами и поэтому изучала, как правило, лишь регулярные (периодич.) К. и волны, то в последнее время усилился интерес к статистич. задачам, связанным с анализом процессов "рождения" статистики в детерминированных системах. В этой части, а также в части исследования сложных колебательных и волновых структур в неравновесных средах современная теория К. и волн перекрывается с синергетикой.
Кинематика колебаний довольно произвольна, однако, если руководствоваться практической или принципиальной важностью тех или иных движений, можно выделить неск. наиболее типичных примеров (рис.). Для простоты будем говорить о К., описываемых ф-цией времени u(t), хотя с кинематич. точки зрения пространств. и временные К. взаимно сводятся друг к другу путём перехода из одной системы отсчёта к другой.
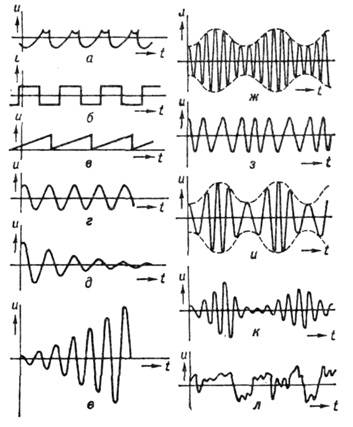
Различные виды колебаний: а - периодические сложной формы; б - прямоугольные; в - пилообразные; г - синусоидальные; д - затухающие; е - нарастающие; ж - амплитудно-модули-рованные; з - частотно-модулированные; и - модулированные по амплитуде и по фазе; к - колебания, амплитуда и фаза которых - случайные функции; л - случайные колебания.
На рис. а - г показаны периодич. К. разл. формы, в к-рых любое значение u(t )повторяется через одинаковые промежутки времени Т, называемые периодом К., т. е. u(t+T) = u (t). Величину, обратную периоду Т и равную числу К. в единицу времени, наз. частотой К.
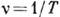 ; часто пользуются также круговой или цик-лич. частотой
; часто пользуются также круговой или цик-лич. частотой 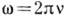 . Обычно частота измеряется в герцах (Гц), что соответствует числу К., совершаемых в 1 с. В случае пространств. К. вводят аналогичные понятия пространств. периода (или длины волны
. Обычно частота измеряется в герцах (Гц), что соответствует числу К., совершаемых в 1 с. В случае пространств. К. вводят аналогичные понятия пространств. периода (или длины волны 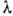 ) и волнового числа
) и волнового числа 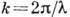
Разновидностями периодич. К. являются прямоугольные меандры (рис., б), пилообразные К. (рис., в )и наиболее важные синусоидальные, или гармонические колебания (рис., г). Последние могут быть записаны в виде
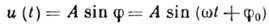
где А - амплитуда,
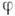 - фаза,
- фаза, 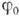 - её нач. значение. B случае строго гармонич. К. величины А,
- её нач. значение. B случае строго гармонич. К. величины А,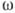 и
и 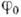 не зависят от времени. Очень употребительна также комплексная запись синусоидальных К.:
не зависят от времени. Очень употребительна также комплексная запись синусоидальных К.:
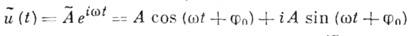
в к-рой комплексная амплитуда
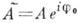 объединяет в себе действит. значения амплитуды и фазы К. В частности, для показанного на рис. д затухающего К.
объединяет в себе действит. значения амплитуды и фазы К. В частности, для показанного на рис. д затухающего К.
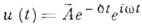
где декремент затухания о можно считать либо мнимой частью частоты
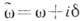 , либо относить к экспоненциально убывающей амплитуде. При отрицат.
, либо относить к экспоненциально убывающей амплитуде. При отрицат. 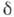 этот коэф. наз. инкрементом, а соответствующее К. превращается в экспоненциально растущее. У К. с убывающей амплитудой периодичность нарушается, но при
этот коэф. наз. инкрементом, а соответствующее К. превращается в экспоненциально растущее. У К. с убывающей амплитудой периодичность нарушается, но при 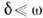 их всё же можно считать почти (квази) периодическими, а при
их всё же можно считать почти (квази) периодическими, а при 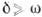 почти апериодическими, т. е. по существу уже не К., а монотонными движениями.
почти апериодическими, т. е. по существу уже не К., а монотонными движениями.
Для передачи информации применяются модулиров. К., амплитуда, фаза или частота к-рых изменяются по закону кодирования информации, напр. в радиовещании высокочастотные К. модулируются К. звуковых частот, передающими речь, музыку. Наиб. употребительными являются модулиров. К. вида u(t) =
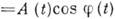 , где амплитуда A (t )медленно изменяется в масштабах периода К., а фаза
, где амплитуда A (t )медленно изменяется в масштабах периода К., а фаза 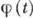 обладает медленно изменяющейся производной, равной мгновенной частоте К., т. е.
обладает медленно изменяющейся производной, равной мгновенной частоте К., т. е. 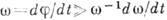 . К. наз. амплитудно-модулированным (рис., ж), если
. К. наз. амплитудно-модулированным (рис., ж), если 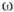 = const,
= const, 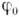 = const. В частности, при синусоидальной модуляции
= const. В частности, при синусоидальной модуляции 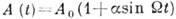 такое К. есть сумма трёх синусоидальных К. с частотами
такое К. есть сумма трёх синусоидальных К. с частотами 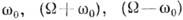 :
:
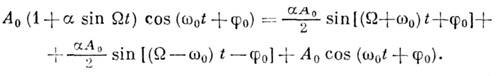
Когда модулирующий сигнал A (t )имеет сложный периодич. характер, то результирующее К. представляется сплошным набором К. всех частот (непрерывный спектр), симметрично сгруппированных около центральной (несущей) частоты
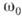 При А =const,
При А =const, 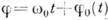 К. наз. модулированным по фазе, а при A=const,
К. наз. модулированным по фазе, а при A=const, 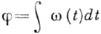 модуляция является частным случаем фазовой. На рис. з и и приведены К., модулированные по амплитуде, частоте и фазе одновременно. Подробнее см. Модулированные колебания.
модуляция является частным случаем фазовой. На рис. з и и приведены К., модулированные по амплитуде, частоте и фазе одновременно. Подробнее см. Модулированные колебания.
При изучении стохастич. процессов приходится иметь дело с частично и полностью случайными К. На рис. к дан пример синусоидального К., модулированного по амплитуде и фазе случайными ф-циями, а на рис. л дана одна из реализаций совершенно неупорядоч. процесса ("белого шума"), к-рый лишь условно можно отнести к К.
Колебат. движения на плоскости или в пространстве в принципе могут быть представлены как совокупность одномерных К. вдоль соответствующих осей координат. Так, два гармонич. колебания (одномерные осцилляторы) с частотами
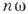 (вдоль оси х )и
(вдоль оси х )и 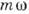 (вдоль оси
(вдоль оси 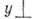 оси х )являются проекциями сложных перио-дич. (при рациональном отношении
оси х )являются проекциями сложных перио-дич. (при рациональном отношении 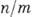 ) плоских К., называемых Лиссажу фигурами. К ним принадлежит и равномерное движение по окружности (ротатор), к-рое можно разложить на два одинаковых синусоидальных К. ( п=т), сдвинутых по фазе на
) плоских К., называемых Лиссажу фигурами. К ним принадлежит и равномерное движение по окружности (ротатор), к-рое можно разложить на два одинаковых синусоидальных К. ( п=т), сдвинутых по фазе на 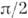 . Именно это обстоятельство составляет одну из причин, по к-рой гармонич. К. оказываются особо выделенными среди других движений в природе. В природе и во мн. техн. устройствах часто возникают движения, почти не отличающиеся (на протяжении больших промежутков времени) от чисто гармонич. или равномерно вращательных. Мн. физ. приборы ( анализаторы спектра) выделяют из произвольных процессов наборы К., близких к гармоническим. Возможна и обратная процедура синтеза гармонич. К., математически соответствующая рядам и интегралам Фурье, в силу к-рой любой временной процесс можно воссоздать сложением или интегрированием гармонич. К. разл. частот и амплитуд.
. Именно это обстоятельство составляет одну из причин, по к-рой гармонич. К. оказываются особо выделенными среди других движений в природе. В природе и во мн. техн. устройствах часто возникают движения, почти не отличающиеся (на протяжении больших промежутков времени) от чисто гармонич. или равномерно вращательных. Мн. физ. приборы ( анализаторы спектра) выделяют из произвольных процессов наборы К., близких к гармоническим. Возможна и обратная процедура синтеза гармонич. К., математически соответствующая рядам и интегралам Фурье, в силу к-рой любой временной процесс можно воссоздать сложением или интегрированием гармонич. К. разл. частот и амплитуд.
Динамика колебаний. Свободные, или собственные, К. являются движением системы, предоставленной самой себе, в отсутствие внеш. воздействий. При малых отклонениях от состояния равновесия движения системы удовлетворяют суперпозиции принципу, согласно к-рому сумма двух произвольных движений также составляет допустимое движение системы; такие движения описываются линейными (в частности, дифференц.) ур-ниями. Если система ещё и консервативна (т. е. в ней нет потерь или притока энергии извне), а её параметры не изменяются во времени (о переменных параметрах будет сказано ниже), то любое собств. К. может быть однозначно представлено как сумма нормальных колебаний, синусоидально изменяющихся во времени с определ. собств. частотами. В колебат. системах с сосредоточенными параметрами, состоящих из N связанных осцилляторов (напр., цепочка из колебат. электрич. контуров или из соединённых упругими пружинками шариков), число нормальных К. (мод) равно N. В системах с распределёнными параметрами (струна, мембрана, полый или открытый резонатор) таких К. существует бесконечное множество. Напр., для струны с закреплёнными концами длиной L моды отличаются числом "полуволн", к-рые можно уложить па всей длине струны:
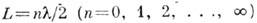 . Если скорость распространения волн вдоль струны равна
. Если скорость распространения волн вдоль струны равна  , то спектр собств. частот определится ф-лой
, то спектр собств. частот определится ф-лой
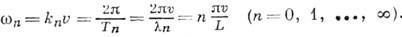
Наличие дисперсии волн [зависимости
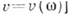 искажает это простое эквидистантное распределение частот, спектр к-рых определится уже из т. н. дисперсионного ур-ния:
искажает это простое эквидистантное распределение частот, спектр к-рых определится уже из т. н. дисперсионного ур-ния: 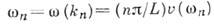 В реальных системах собственные К. оудут затухать из-за потерь, поэтому их можно считать приближённо гармоническими лишь в интервале времени, меньшем
В реальных системах собственные К. оудут затухать из-за потерь, поэтому их можно считать приближённо гармоническими лишь в интервале времени, меньшем 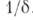 Затухающее К. (рис., д )может быть представлено в виде пакета гармонич. К., непрерывно заполняющих интервал частот
Затухающее К. (рис., д )может быть представлено в виде пакета гармонич. К., непрерывно заполняющих интервал частот 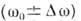 (интеграл Фурье), тем более узком, чем меньше
(интеграл Фурье), тем более узком, чем меньше 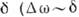 ). В этом случае говорят
). В этом случае говорят
Наличие дисперсии волн [зависимости
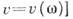 искажает это простое эквидистантное распределение частот, спектр к-рых определится уже из т. н. дисперсионного ур-ния:
искажает это простое эквидистантное распределение частот, спектр к-рых определится уже из т. н. дисперсионного ур-ния: 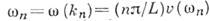 . В реальных системах собственные К. будут затухать из-за потерь, поэтому их можно считать приближённо гармоническими лишь в интервале времени, меньшем
. В реальных системах собственные К. будут затухать из-за потерь, поэтому их можно считать приближённо гармоническими лишь в интервале времени, меньшем 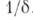 Затухающее К. (рис., д )может быть представлено в виде пакета гармонич. К., непрерывно заполняющих интервал частот
Затухающее К. (рис., д )может быть представлено в виде пакета гармонич. К., непрерывно заполняющих интервал частот 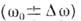 (интеграл Фурье), тем более узком, чем меньше
(интеграл Фурье), тем более узком, чем меньше 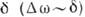 . В этом случае говорят об уширении спектральной линии, иногда характеризуя её добротностью
. В этом случае говорят об уширении спектральной линии, иногда характеризуя её добротностью 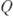 , равной отношению запасённой энергии W к потерям Р за период колебаний
, равной отношению запасённой энергии W к потерям Р за период колебаний 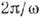 , т. е.
, т. е. 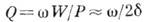 . Т. о., сгущение спектра из-за потерь влечёт за собой превращение дискретного спектра в сплошной, когда ширина линий становится прибл. равной интервалу между ними, т. е.
. Т. о., сгущение спектра из-за потерь влечёт за собой превращение дискретного спектра в сплошной, когда ширина линий становится прибл. равной интервалу между ними, т. е.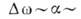
Собств.
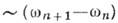 К. нелинейных систем менее доступны для классификации. Нелинейность систем с дискретным спектром собств. частот приводит к "перекачке" энергии К. по спектральным компонентам; при этом возникают процессы конкуренции мод - выживание одних п подавление других. Дисперсии могут стабилизировать эти процессы и привести к формированию устойчивых пространственно-временных образований, примерами к-рых в системах с непрерывным спектром являются солитоны.
К. нелинейных систем менее доступны для классификации. Нелинейность систем с дискретным спектром собств. частот приводит к "перекачке" энергии К. по спектральным компонентам; при этом возникают процессы конкуренции мод - выживание одних п подавление других. Дисперсии могут стабилизировать эти процессы и привести к формированию устойчивых пространственно-временных образований, примерами к-рых в системах с непрерывным спектром являются солитоны.
Возбуждение колебаний происходит либо путём непосредств. воздействия на состояние колебат. системы (раскачка маятника периодич. толчками, включение периодич. эдс в колебат. контур и т. д.), либо путём периодич. изменения параметров этой системы (длины подвеса маятника, ёмкости или самоиндукции контура, коэф. упругости струны и т. п.), либо благодаря "самовозбуждению" К., т. е. возникновению колебат. движений внутри самой системы. В первом случае говорят о вынужденных колебаниях, во втором - о параметрич. возбуждении колебаний, а в третьем - об автоколебаниях.
Особое значение при возбуждении К. имеет явление резонанса, состоящее в резком увеличении отклика системы (амплитуды К.) при приближении частоты внеш. воздействия к нек-рой резонансной частоте, характеризующей систему. Если последняя линейна и параметры её не зависят от времени, то резонансные частоты совпадают с частотами её собственных К. и соответствующий отклик тем сильнее, чем выше добротность колебат. системы. Раскачка происходит до тех пор, пока энергия, вносимая извне (напр., при каждом отклонении маятника), превышает потери за период осцилляции. Для линейных К. энергия, получаемая от источника, пропорциональна первой степени амплитуды, а потери растут пропорционально её квадрату, поэтому баланс энергий всегда достижим.
При больших амплитудах К. становятся нелинейными, происходит смещение собств. частот системы и обогащение их спектра гармониками и субгармониками. Ограничение амплитуды К. может быть обусловлено как нелинейной диссипацией энергии, так и уходом системы из резонанса. При возбуждении К. в системах с распределёнными параметрами макс. амплитуды достигаются в случае пространственновременного резонанса, когда не только частота внеш. воздействия, но его распределение по координатам хорошо "подогнаны" к структуре нормальной моды или, на языке бегущих волн, когда наступает не только совмещение их частот (резонанс), но и волновых векторов (синхронизм).
Существует нек-рый выделенный класс вынужденных К., при к-ром внеш. воздействие, не являясь чисто колебательным, имеет, однако, настолько богатый частотный спектр, что в нём всегда содержатся резонансные частоты. Напр., заряж. частица, пролетающая между двумя плоскостями, возбуждает почти весь набор нормальных волн и К., свойственный этой системе. Сюда же следует отнести черенковское излучение (см. Черенкоеа-Вавилова излучение )или тормозное излучение частицы в однородных средах, когда и спектр внеш. воздействия и спектр собств. К.- оба сплошные, т. е. в них представлены все возможные частоты. Наконец, есть и совсем аномальный случай вынужденных К. в системах с непрерывным спектром собств. частот типа ротатора (маховик, колесо, электрон в магн. поле и др.), где вращат. движение (а следовательно, и два ортогональных колебат. движения) может возбуждаться силами, неизменными во времени.
Параметрич. возбуждение К. происходит в результате развития т. н. параметрич. неустойчивости, возникающей при периодич. воздействии на те параметры системы, к-рые определяют величину запасённой колебат. энергии; в электрич. контуре - это самоиндукция или ёмкость (но не сопротивление), у маятника - это длина нити или масса груза (но не коэф. трения). Если в такой системе случайно (напр., из-за тепловых флуктуации) "зародились" К. с ничтожно малой амплитудой на собственной частоте
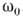 , то, как и любые свободные К., они сопровождаются пульсацией энергии с удвоенной частотой
, то, как и любые свободные К., они сопровождаются пульсацией энергии с удвоенной частотой 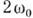 . Если при этом какими-то внеш. (не зависящими от движения в системе) средствами периодически изменять подходящий параметр системы (напр., ёмкость конденсатора или длину подвеса маятника), то начнёт изменяться и запасённая энергия: увеличиваться или уменьшаться в зависимости от знака работы, совершаемой внеш. силой над параметром, т. е. от того, в какой фазе по отношению к силе происходят К. энергии в системе. "Выживет" и будет расти только такое К., фаза к-рого благоприятствует накачке энергии в систему. Возникшие в иных фазах К. либо сохранят свою амплитуду, либо будут затухать (в последнем случае говорят о параметрич. успокоении К.).
. Если при этом какими-то внеш. (не зависящими от движения в системе) средствами периодически изменять подходящий параметр системы (напр., ёмкость конденсатора или длину подвеса маятника), то начнёт изменяться и запасённая энергия: увеличиваться или уменьшаться в зависимости от знака работы, совершаемой внеш. силой над параметром, т. е. от того, в какой фазе по отношению к силе происходят К. энергии в системе. "Выживет" и будет расти только такое К., фаза к-рого благоприятствует накачке энергии в систему. Возникшие в иных фазах К. либо сохранят свою амплитуду, либо будут затухать (в последнем случае говорят о параметрич. успокоении К.).
Параметрич. возбуждение К. происходит с наиб, эффективностью при равенстве частоты изменения параметра удвоенной собственной частоте
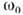 . Сама же система остаётся линейной: движения в пей хотя и не синусоидальны, но подчинены принципу суперпозиции. Параметрич. раскачка К. (т. н. параметрич. резонанс) возможна и на частотах, дробно-кратных собств. частоте
. Сама же система остаётся линейной: движения в пей хотя и не синусоидальны, но подчинены принципу суперпозиции. Параметрич. раскачка К. (т. н. параметрич. резонанс) возможна и на частотах, дробно-кратных собств. частоте 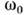 одиночного колебат. контура, а также на комбинац. частотах в системах с неск. степенями свободы
одиночного колебат. контура, а также на комбинац. частотах в системах с неск. степенями свободы 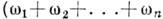 =0), в т. ч. и в системах с распредел. параметрами при выполнении условий синхронизма возбуждаемых волн с волной накачки. См. также Параметрические колебательные системы. Параметрический резонанс.
=0), в т. ч. и в системах с распредел. параметрами при выполнении условий синхронизма возбуждаемых волн с волной накачки. См. также Параметрические колебательные системы. Параметрический резонанс.
Любую нелинейную колебат. систему можно рассматривать как самосогласованную параметрич. систему, в к-рую введён "элемент" обратной связи, как бы осуществляющий "самоуправление" параметром. При определ. условиях в такой системе могут возникать непрекращающиеся самоподдерживающиеся К., или автоколебания, при к-рых внеш. источнику отводится лишь ф-ция восполнения потерь энергии на диссипацию. Процесс формирования автоколебаний обычно состоит в последовательном самосогласовании движений. Пусть нач. состояние системы неустойчиво - либо по отношению к ничтожно малым флуктуа-циям (мягкий режим возбуждения), либо по отношению к определ. конечным возмущениям (жёсткий режим возбуждения). В любом случае спонтанно (случайно) возникшее К. начнёт увеличиваться по амплитуде (процесс усиления К.). Эти усиленные К. через элемент положит. обратной связи, обеспечивающий самосогласованность фаз, снова "подаются" в место своего возникновения и снова усиливаются и т. д. Получается очень быстрый (чаще всего экспоненциальный) рост К. Ограничение наступает из-за конечности энергетич. ресурсов, а иногда и раньше - из-за рассогласованности фаз (подробнее см. Автоколебания). Методически удобное "расчленение" автоколебат. системы на элементы, осуществляющие усиление, обратную связь и ограничение К., в общем случае не может быть однозначно сопоставлено с определенными функционально автономными узлами. Так, в одном из самых старинных автоколебат. устройств - в маятниковых часах - ф-ции обратной связи, усилителя и ограничителя выполняет единый узел-балансир с анкером.
Автоколебат. системы обладают большим разнообразием поведения (периодические, многопериодические, стохастические) и широко представлены как в природе, так и в технике: радиотехн., акустич., оптич., квантовые (лазеры) генераторы, генераторы с сосре-доточ. и распредел. параметрами, механич. автоколебат. системы - часы, ветровые волны на воде, турбулентные процессы в аэро- и гидродинамике, флаттер крыльев самолётов и др. Часто встречаются более сложные автоколебат. системы, где происходит взаимная синхронизация колебаний или стохастизация К.: стимуляция (пейсмейкер, от англ, pacemaker) сердца, синхронизация мод в лазерах, индуцированные излучатели эл.-магн. волн, переход к турбулентности в гидродинамич. течениях вязкой жидкости, рождение шума в системах связанных генераторов и т. д.
К. могут быть самого широкого диапазона частот
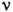 и периодов Т. Так, приведём, напр., значения Т или
и периодов Т. Так, приведём, напр., значения Т или 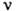 для нек-рых важнейших К. и вращений: обращение Солнца вокруг центра Галактики
для нек-рых важнейших К. и вращений: обращение Солнца вокруг центра Галактики 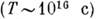 ; ледниковые периоды на Земле
; ледниковые периоды на Земле 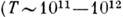 с): наибольший цикл солнечной активности
с): наибольший цикл солнечной активности 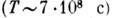 : обращение Земли вокруг Солнца - год
: обращение Земли вокруг Солнца - год 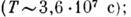 ~ обращение Луны вокруг Земли - лунный месяц
~ обращение Луны вокруг Земли - лунный месяц 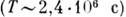 ; вращение Земли вокруг своей оси - сутки
; вращение Земли вокруг своей оси - сутки 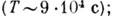 оборот часовой стрелки
оборот часовой стрелки 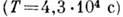 ; оборот минутной стрелки
; оборот минутной стрелки 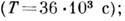 ветровые волны на море
ветровые волны на море 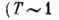 с или
с или 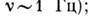 опасные для человека инфразвуки
опасные для человека инфразвуки 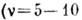 Гц); колесо автомобиля при скорости 60 км/ч
Гц); колесо автомобиля при скорости 60 км/ч 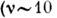 Гц); звуковые волны, воспринимаемые человеком на слух (
Гц); звуковые волны, воспринимаемые человеком на слух (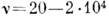 Гц); стандартная частота колебаний перем. тока (
Гц); стандартная частота колебаний перем. тока (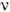 =50 Гц); УЗ (
=50 Гц); УЗ (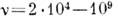 Гц); эл.-магн. колебания радиодиапазона (
Гц); эл.-магн. колебания радиодиапазона (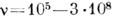 Гц); эл.-магн. колебания СВЧ-диапазона (
Гц); эл.-магн. колебания СВЧ-диапазона (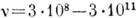 ); гиперзвук (
); гиперзвук (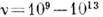 Гц); оптика (видимый свет) (
Гц); оптика (видимый свет) (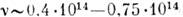 , Гц); УФ-излучение (
, Гц); УФ-излучение (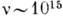 - 1017 Гц); рентг. излучение (
- 1017 Гц); рентг. излучение (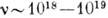 Гц); гамма-лучи (
Гц); гамма-лучи (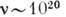 Гц); короткоживущие частицы-резо-нансы (
Гц); короткоживущие частицы-резо-нансы (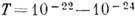 с).
с).
Лит.: Андронов А. А., В и т т А. А., X а й-кин С. Э., Теория колебаний, [3 изд.], М., 1981; Стретт Д ж. В. (лорд Рэлей), Теория звука, пер. с англ., 2 изд., т. 1 - 2, М., 1955; Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Бишоп Р., Колебания, пер. с англ., 3 изд., М., 1986. М. А. Миллер, М. И. Рабинович.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.