- ОБМЕННОЕ ВЗАИМОДЕЙСТВИЕ
-
специфич. взаимное влияние тождественных частиц, эффективно проявляющееся как результат нек-рого особого вз-ствия. О. в.— чисто квантовомеханич. эффект, не имеющий аналога в классич. физике (см. КВАНТОВАЯ МЕХАНИКА).Вследствие квантовомеханич. принципа неразличимости одинаковых ч-ц (тождественности принципа) волн. ф-ция системы должна обладать определ. симметрией относительно перестановки двух таких ч-ц, т. е. их координат и проекций спинов: для ч-ц с целым спином — бозонов — волн. ф-ция системы не меняется при такой перестановке (явл. симметричной), а для ч-ц с полуцелым спином — фермионов — меняет знак (явл. антисимметричной). Если силы вз-ствия между ч-цами не зависят от их спинов, волн. ф-цию системы можно представить в виде произведения двух ф-ций, одна из к-рых зависит только от координат ч-ц, а другая — только от их спинов. В этом случае из принципа тождественности следует, что координатная часть волн. ф-ции, описывающая движение ч-ц в пр-ве, должна обладать определ. симметрией относительно перестановки координат одинаковых ч-ц, зависящей от симметрии спиновой части волн. ф-ции. Наличие такой симметрии означает, что имеет место определ. согласованность, корреляция движения одинаковых ч-ц, к-рая сказывается на энергии системы (даже в отсутствие силовых вз-ствий между ч-цами). Поскольку обычно влияние ч-ц друг на друга явл. результатом действия между ними к.-л. сил, о взаимном влиянии одинаковых ч-ц, вытекающем из принципа тождественности, говорят как о проявлении специфич. вз-ствия — О. в.Возникновение О. в. можно проиллюстрировать на примере атома гелия (впервые это было сделано нем. физиком В. Гейзенбергом в 1926). Спиновые вз-ствия в лёгких атомах малы, поэтому волн. ф-ция y двух эл-нов в атоме гелия может быть представлена в виде:y=Ф(r1, r2)c(s1, s2), (1)где Ф (r1, r2) — ф-ция координат r1, r2 эл-нов, а c(s1, s2) — ф-ция проекций их спинов s1, s2 на нек-рое направление. Т. к. эл-ны явл.. фермионами, полная волн. ф-ция y должна быть антисимметричной. Если суммарный спин S обоих эл-нов равен нулю (спины антипараллельны — парагелий), то спиновая ф-ция c антисимметрична относительно перестановки спиновых переменных и, следовательно, координатная ф-ция Ф должна быть симметричной относительно перестановки координат эл-нов. Если же S=1 (спины параллельны — ортогелий), то c симметрична, а Ф — антисимметрична. Обозначая через yn(r1), ym(r2) волн ф-ции отд. эл-нов в атоме гелия (индексы га и т означают набор квант. чисел, определяющих состояние эл-на в атоме), можно, пренебрегая сначала вз-ствием между эл-нами, записать координатную часть волн. ф-ции в виде: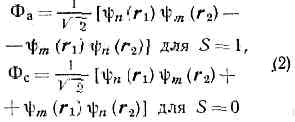 (множитель 1/?2 введён для нормировки волн. ф-ции). В состоянии с антисимметричной координатной ф-цией Фа ср. расстояние между эл-нами оказывается большим, чем в состоянии с симметричной ф-цией Фс; это видно из того, что вероятность |y|2=|Фа|2|cс|2 нахождения эл-нов в одной и той же точке r1=r2 для состояния Фа равна нулю. Поэтому ср. энергия кулоновского вз-ствия (отталкивания) двух эл-нов оказывается в состоянии Фа меньшей, чем в состоянии Фс. Поправка к энергии системы, связанная с вз-ствием эл-нов, определяется по теории возмущений и равна?вз =K±А, (3)где знаки ± относятся соответственно к симметричному и антисимметричному координатным состояниям
(множитель 1/?2 введён для нормировки волн. ф-ции). В состоянии с антисимметричной координатной ф-цией Фа ср. расстояние между эл-нами оказывается большим, чем в состоянии с симметричной ф-цией Фс; это видно из того, что вероятность |y|2=|Фа|2|cс|2 нахождения эл-нов в одной и той же точке r1=r2 для состояния Фа равна нулю. Поэтому ср. энергия кулоновского вз-ствия (отталкивания) двух эл-нов оказывается в состоянии Фа меньшей, чем в состоянии Фс. Поправка к энергии системы, связанная с вз-ствием эл-нов, определяется по теории возмущений и равна?вз =K±А, (3)где знаки ± относятся соответственно к симметричному и антисимметричному координатным состояниям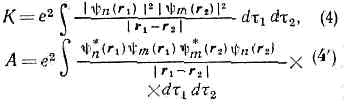 (е — заряд эл-на, dt=dxdydz — элемент объёма). Величина К имеет наглядный классич. смысл и соответствует электростатич. вз-ствию двух заряж. «облаков» с плотностями заряда e|yn(r1)|2 и e|ym(r2)|2. Величину А, называемую обменным интегралом, можно интерпретировать как электростатич. вз-ствие заряж. «облаков» с плотностями заряда ey*n(r1)ym(r1) и ey*m(r2)yn(r2) (звёздочка означает комплексное сопряжение), т. е. когда каждый из эл-нов находится одновременно в состояниях yn и ym (что бессмысленно с точки зрения классич. физики). Из (3) следует, что полная энергия пара- и ортогелия с эл-нами в аналогичных состояниях отличается на величину 2А. Т. о., хотя непосредственно спиновое вз-ствие мало и не учитывается, тождественность двух эл-нов в атоме гелия приводит к тому, что энергия системы оказывается зависящей от полного спина системы, как если бы между ч-цами существовало дополнит., обменное, вз-ствие. Очевидно, что О. в. в данном случае явл. частью кулоновского вз-ствия эл-нов и явным образом выступает при приближённом рассмотрении квантовомеханич. системы, когда волн. ф-ция всей системы выражается через волн. ф-ции отд. ч-ц (в частности, в приближении Хартри — Фока; (см. САМОСОГЛАСОВАННОЕ ПОЛЕ)).О. в. эффективно проявляется в тех случаях, когда «перекрываются» волн. ф-ции отд. ч-ц системы, т. е. когда существуют области пр-ва, в к-рых с заметной вероятностью может находиться ч-ца в разл. состояниях движения. Это видно из выражения для обменного интеграла А: если степень перекрытия состояний y*n (r) и ym(r) незначительна, то величина А очень мала.Из принципа тождественности следует, что О. в. возникает в системе одинаковых ч-ц даже в случае, если прямыми силовыми вз-ствиями ч-ц можно пренебречь, т. е. в идеальном газе тождеств. ч-ц. Эффективно оно начинает проявляться, когда ср. расстояние между ч-цами становится сравнимым (или меньшим) с длиной волны де Бройля, соответствующей ср. скорости ч-ц. При этом хар-р О. в. различен для фермионов и для бозонов. Для фермионов О. в. явл. следствием Паули принципа, препятствующего сближению тождеств. ч-ц с одинаковым направлением спинов, и эффективно проявляется как отталкивание их друг от друга на расстояниях порядка или меньше длины волны де Бройля; отличие от нуля энергии вырожденного газа фермионов (ферми-газа) целиком обусловлено таким О. в. В системе тождеств. бозонов О. в., напротив, имеет хар-р взаимного притяжения ч-ц. В этих случаях рассмотрение систем, состоящих из большего числа одинаковых ч-ц, производится на основе Ферми — Дирака статистики для фермнонов и Бозе — Эйнштейна статистики для бозонов.Если взаимодействующие тождеств. ч-цы находятся во внеш. поле, напр. в кулоновском поле ядра, то существование определённой симметрии волн. ф-ции и соответственно определ. корреляции движения ч-ц влияет на их энергию в этом поле, что также явл. обменным эффектом. Обычно (в атоме, молекуле, кристалле) это О. в. вносит вклад обратного знака по сравнению с вкладом О. в. ч-ц друг с другом. Поэтому суммарный обменный эффект может как понижать, так и повышать полную энергию вз-ствия в системе. Энергетич. выгодность или невыгодность состояния с параллельными спинами фермионов, в частности эл-нов, зависит от относит. величин этих вкладов. Так, в ферромагнетике (аналогично рассмотренному атому гелия) более низкой энергией обладает состояние, в к-ром спины (а следовательно, и магн. моменты) эл-нов в незаполненных оболочках соседних атомов параллельны; в этом случае благодаря О. в. возникает спонтанная намагниченность (см. ФЕРРОМАГНЕТИЗМ). Напротив, в молекулах с ковалентной хим. связью, напр. в молекуле Н2, энергетически выгодно состояние, в к-ром спины валентных эл-нов соединяющихся атомов антипараллельны.О. в. объясняет, т. о., закономерности ат. и мол. спектроскопии, хим. связь в молекулах, ферромагнетизм (и антиферромагнетизм), а также др. специфич. явления в системах одинаковых ч-ц.
(е — заряд эл-на, dt=dxdydz — элемент объёма). Величина К имеет наглядный классич. смысл и соответствует электростатич. вз-ствию двух заряж. «облаков» с плотностями заряда e|yn(r1)|2 и e|ym(r2)|2. Величину А, называемую обменным интегралом, можно интерпретировать как электростатич. вз-ствие заряж. «облаков» с плотностями заряда ey*n(r1)ym(r1) и ey*m(r2)yn(r2) (звёздочка означает комплексное сопряжение), т. е. когда каждый из эл-нов находится одновременно в состояниях yn и ym (что бессмысленно с точки зрения классич. физики). Из (3) следует, что полная энергия пара- и ортогелия с эл-нами в аналогичных состояниях отличается на величину 2А. Т. о., хотя непосредственно спиновое вз-ствие мало и не учитывается, тождественность двух эл-нов в атоме гелия приводит к тому, что энергия системы оказывается зависящей от полного спина системы, как если бы между ч-цами существовало дополнит., обменное, вз-ствие. Очевидно, что О. в. в данном случае явл. частью кулоновского вз-ствия эл-нов и явным образом выступает при приближённом рассмотрении квантовомеханич. системы, когда волн. ф-ция всей системы выражается через волн. ф-ции отд. ч-ц (в частности, в приближении Хартри — Фока; (см. САМОСОГЛАСОВАННОЕ ПОЛЕ)).О. в. эффективно проявляется в тех случаях, когда «перекрываются» волн. ф-ции отд. ч-ц системы, т. е. когда существуют области пр-ва, в к-рых с заметной вероятностью может находиться ч-ца в разл. состояниях движения. Это видно из выражения для обменного интеграла А: если степень перекрытия состояний y*n (r) и ym(r) незначительна, то величина А очень мала.Из принципа тождественности следует, что О. в. возникает в системе одинаковых ч-ц даже в случае, если прямыми силовыми вз-ствиями ч-ц можно пренебречь, т. е. в идеальном газе тождеств. ч-ц. Эффективно оно начинает проявляться, когда ср. расстояние между ч-цами становится сравнимым (или меньшим) с длиной волны де Бройля, соответствующей ср. скорости ч-ц. При этом хар-р О. в. различен для фермионов и для бозонов. Для фермионов О. в. явл. следствием Паули принципа, препятствующего сближению тождеств. ч-ц с одинаковым направлением спинов, и эффективно проявляется как отталкивание их друг от друга на расстояниях порядка или меньше длины волны де Бройля; отличие от нуля энергии вырожденного газа фермионов (ферми-газа) целиком обусловлено таким О. в. В системе тождеств. бозонов О. в., напротив, имеет хар-р взаимного притяжения ч-ц. В этих случаях рассмотрение систем, состоящих из большего числа одинаковых ч-ц, производится на основе Ферми — Дирака статистики для фермнонов и Бозе — Эйнштейна статистики для бозонов.Если взаимодействующие тождеств. ч-цы находятся во внеш. поле, напр. в кулоновском поле ядра, то существование определённой симметрии волн. ф-ции и соответственно определ. корреляции движения ч-ц влияет на их энергию в этом поле, что также явл. обменным эффектом. Обычно (в атоме, молекуле, кристалле) это О. в. вносит вклад обратного знака по сравнению с вкладом О. в. ч-ц друг с другом. Поэтому суммарный обменный эффект может как понижать, так и повышать полную энергию вз-ствия в системе. Энергетич. выгодность или невыгодность состояния с параллельными спинами фермионов, в частности эл-нов, зависит от относит. величин этих вкладов. Так, в ферромагнетике (аналогично рассмотренному атому гелия) более низкой энергией обладает состояние, в к-ром спины (а следовательно, и магн. моменты) эл-нов в незаполненных оболочках соседних атомов параллельны; в этом случае благодаря О. в. возникает спонтанная намагниченность (см. ФЕРРОМАГНЕТИЗМ). Напротив, в молекулах с ковалентной хим. связью, напр. в молекуле Н2, энергетически выгодно состояние, в к-ром спины валентных эл-нов соединяющихся атомов антипараллельны.О. в. объясняет, т. о., закономерности ат. и мол. спектроскопии, хим. связь в молекулах, ферромагнетизм (и антиферромагнетизм), а также др. специфич. явления в системах одинаковых ч-ц.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ОБМЕННОЕ ВЗАИМОДЕЙСТВИЕ
-
- специфич. взаимное влияние одинаковых (тождественных) частиц, эффективно проявляющеесякак результат нек-рого особого взаимодействия. О. в. - чисто квантовомеханич. эффект, не имеющий аналога в классич. физике (см. Квантовая механика).
Вследствие квантовомеханич. принципа неразличимостиодинаковых частиц ( тождественности принципа )волновая ф-ция системыдолжна обладать определённой симметрией относительно перестановки двухтаких частиц, т. е. их координат и проекций спинов: для частиц с целымспином - бозонов - волновая ф-ция системы не меняется при такой перестановке(является симметричной), а для частиц с полуцелым спином - фермионов -меняет знак (является антисимметричной). Если силы взаимодействия междучастицами не зависят от их спинов, волновую ф-цию системы можно представитьв виде произведения двух ф-ций, одна из к-рых зависит только от координатчастиц, а другая - только от их спинов. В этом случае из принципа тождественностиследует, что координатная часть волновой ф-цип, описывающая движение частицв пространстве, должна обладать определённой симметрией относительно перестановкикоординат одинаковых частиц, зависящей от симметрии спиновой части волновойф-ции. Наличие такой симметрии означает, что имеет место определённая согласованность, корреляция движения одинаковых частиц, к-рая сказывается на энергии системы(даже в отсутствие силовых взаимодействий между частицами). Поскольку обычновлияние частиц друг на друга является результатом действия между ними к.-л. сил, о взаимном влиянии одинаковых частиц, вытекающем из принципа тождественности, говорят как о проявлении специфич. взаимодействия - О. в.
Возникновение О. в. можно проиллюстрироватьна примере атома гелия [впервые это было сделано В. Гейзенбергом (W. Heisenberg)в 1920]. Спиновые взаимодействия в лёгких атомах малы, поэтому волноваяф-ция двух электронов в атоме гелия может быть представлена в виде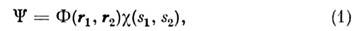
где Ф(r1,r2)- ф-ция координат электронов,
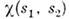 - ф-ция проекций их спинов на нек-рое направление. Т. к. электроны являютсяфермионамн, полная волновая ф-ция должна быть антисимметричной. Если суммарныйспин S обоих электронов равен нулю (спины антипараллельны - парагелий),то спиновая ф-ция
- ф-ция проекций их спинов на нек-рое направление. Т. к. электроны являютсяфермионамн, полная волновая ф-ция должна быть антисимметричной. Если суммарныйспин S обоих электронов равен нулю (спины антипараллельны - парагелий),то спиновая ф-ция 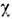 антисимметрична относительно перестановки спиновых переменных и, следовательно, координатная ф-ция Ф должна быть симметрична относительно перестановкикоординат электронов. Если же S =1 (спины параллельны - ортогелий),то
антисимметрична относительно перестановки спиновых переменных и, следовательно, координатная ф-ция Ф должна быть симметрична относительно перестановкикоординат электронов. Если же S =1 (спины параллельны - ортогелий),то 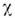 симметрична, а Ф антисимметрична. Обозначая через
симметрична, а Ф антисимметрична. Обозначая через 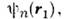
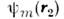 волновые ф-ции отд. электронов в атоме гелия (индексы n, т означаютнабор квантовых чисел, определяющих состояние электрона в атоме), можно, пренебрегая сначала взаимодействием между электронами, записать координатнуючасть волновой ф-ции в виде
волновые ф-ции отд. электронов в атоме гелия (индексы n, т означаютнабор квантовых чисел, определяющих состояние электрона в атоме), можно, пренебрегая сначала взаимодействием между электронами, записать координатнуючасть волновой ф-ции в виде 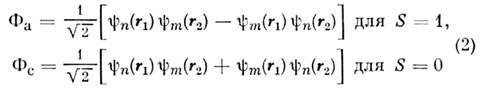
(множитель
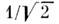 введён для нормировки волновой ф-ции). В состоянии с антисимметричной координатнойф-цией Ф а ср. расстояние между электронами оказывается большим, чем в состоянии с симметричной ф-цией Ф с; это видно из того, что вероятность
введён для нормировки волновой ф-ции). В состоянии с антисимметричной координатнойф-цией Ф а ср. расстояние между электронами оказывается большим, чем в состоянии с симметричной ф-цией Ф с; это видно из того, что вероятность 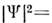 =
=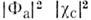 нахожденияэлектронов в одной и той же точке (r1 = r2) для состоянияФ а равна нулю. Поэтому ср. энергия кулоновского взаимодействия(отталкивания) двух электронов оказывается в состоянии Ф а меньшей, чем в состоянии Ф с. Поправка к энергии системы, связанная свзаимодействием электронов, определяется по теории возмущений:
нахожденияэлектронов в одной и той же точке (r1 = r2) для состоянияФ а равна нулю. Поэтому ср. энергия кулоновского взаимодействия(отталкивания) двух электронов оказывается в состоянии Ф а меньшей, чем в состоянии Ф с. Поправка к энергии системы, связанная свзаимодействием электронов, определяется по теории возмущений: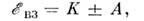 (3)
(3)где знаки
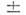 относятсясоответственно к симметричному и антисимметричному координатным состояниям,
относятсясоответственно к симметричному и антисимметричному координатным состояниям,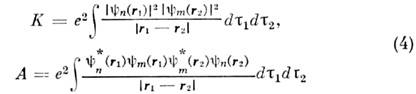
( е - заряд электрона,
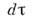 - dxdydz - элемент объёма). Величина К имеет наглядный классич. смысл и соответствует электростатич. взаимодействию двух заряж. "облаков"с плотностями заряда
- dxdydz - элемент объёма). Величина К имеет наглядный классич. смысл и соответствует электростатич. взаимодействию двух заряж. "облаков"с плотностями заряда 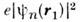 и
и 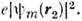 Величину А, называемуюобменным интегралом, можно интерпретировать как электростатич. взаимодействиезаряж. "облаков" с плотностями заряда
Величину А, называемуюобменным интегралом, можно интерпретировать как электростатич. взаимодействиезаряж. "облаков" с плотностями заряда 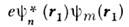 и
и 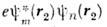 (звёздочкаозначает комплексное сопряжение), т. е. когда каждый из электронов находитсяодновременно в состояниях
(звёздочкаозначает комплексное сопряжение), т. е. когда каждый из электронов находитсяодновременно в состояниях 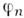 и
и 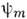 (чтобессмысленно с точки зрения классич. физики). Из (3) следует, что полнаяэнергия пара- и ортогелия с электронами в аналогичных состояниях отличаетсяна величину 2 А. Т. о., хотя непосредственно спиновое взаимодействиемало и не учитывается, тождественность двух электронов в атоме гелия приводитк тому, что энергия системы оказывается зависящей от полного спина системы, как если бы между частицами существовало дополнительное, обменное взаимодействие. Очевидно, что О. в. в данном случае является частью кулоновского взаимодействияэлектронов и явным образом выступает при приближённом рассмотрении квантовомеханич. системы, когда волновая ф-ция всей системы выражается через волновые ф-цииотд. частиц (в частности, в приближении Хартри - Фока; см. Хартри -Фока метод). О. в. эффективно проявляется в тех случаях, когда "перекрываются"волновые ф-ции отд. частиц системы, т. е. когда существуют области пространства, в к-рых с заметной вероятностью может находиться частица в разл. состоянияхдвижения. Это видно из выражения для обменного интеграла А: еслистепень перекрытия состояний
(чтобессмысленно с точки зрения классич. физики). Из (3) следует, что полнаяэнергия пара- и ортогелия с электронами в аналогичных состояниях отличаетсяна величину 2 А. Т. о., хотя непосредственно спиновое взаимодействиемало и не учитывается, тождественность двух электронов в атоме гелия приводитк тому, что энергия системы оказывается зависящей от полного спина системы, как если бы между частицами существовало дополнительное, обменное взаимодействие. Очевидно, что О. в. в данном случае является частью кулоновского взаимодействияэлектронов и явным образом выступает при приближённом рассмотрении квантовомеханич. системы, когда волновая ф-ция всей системы выражается через волновые ф-цииотд. частиц (в частности, в приближении Хартри - Фока; см. Хартри -Фока метод). О. в. эффективно проявляется в тех случаях, когда "перекрываются"волновые ф-ции отд. частиц системы, т. е. когда существуют области пространства, в к-рых с заметной вероятностью может находиться частица в разл. состоянияхдвижения. Это видно из выражения для обменного интеграла А: еслистепень перекрытия состояний 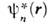 и
и 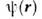 незначительна, то величина А очень мала.
незначительна, то величина А очень мала.
Из принципа тождественности следует, чтоО. в. возникает в системе одинаковых частиц даже в случае, если прямымисиловыми взаимодействиями частиц можно пренебречь, т. е. в идеальном газетождеств. частиц. Эффективно оно начинает проявляться, когда ср. расстояние . междучастицами становится сравнимым (или меньшим) с длиной волны де Бройля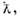 соответствующейср. скорости частиц. Поскольку
соответствующейср. скорости частиц. Поскольку 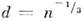 (где п - концентрация частиц), а
(где п - концентрация частиц), а 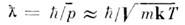 (где
(где 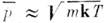 - ср. импульс, т - масса частиц, Т- абс. темп-pa), условие
- ср. импульс, т - масса частиц, Т- абс. темп-pa), условие 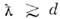 даёт простой критерий "включения" О. в. в идеальном газе:
даёт простой критерий "включения" О. в. в идеальном газе: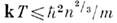 (условие вырождения).
(условие вырождения).
Характер О. в. различен для фермионови для бозонов. Для фермионов О. в. является следствием Паули принципа, препятствующегосближению тождеств. частиц с одинаковым направлением спинов, и эффективнопроявляется как отталкивание их друг от друга на расстояниях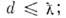 отличие от нуля энергии вырожденного газа фермионов (ферми-газа)целиком обусловлено таким О. в. Для сильно сжатого вещества, когда . значительноменьше размеров атомов (но больше ядерных), О. в. электронов (отталкивание)обусловливает оси. вклад в давление при "низких" темн-рах, удовлетворяющихусловию вырождения. Такие условия осуществляются в звёздах типа белыхкарликов.
отличие от нуля энергии вырожденного газа фермионов (ферми-газа)целиком обусловлено таким О. в. Для сильно сжатого вещества, когда . значительноменьше размеров атомов (но больше ядерных), О. в. электронов (отталкивание)обусловливает оси. вклад в давление при "низких" темн-рах, удовлетворяющихусловию вырождения. Такие условия осуществляются в звёздах типа белыхкарликов.
В системе тождеств. бозонов О. в., напротив, имеет характер взаимного притяжения частиц. Рассмотрение систем из большегочисла одинаковых частиц производится на основе Ферми - Дирака статистики дляфермионов и Бозе - Эйнштейна статистики для бозонов.
Если взаимодействующие тождеств. частицынаходятся во внеш. поле, напр. в кулоновском поле ядра, то существованиеопределённой симметрии волновой ф-ции и соответственно определённой корреляциидвижения частиц влияет на их энергию в этом поле, что также является обменнымэффектом. Обычно (в атоме, молекуле, кристалле) это О. в. вносит вкладобратного знака по сравнению с вкладом О. в. частиц друг с другом. Поэтомусуммарный обменный эффект может как понижать, так и повышать полную энергиювзаимодействия в системе. Энергетич. выгодность или невыгодность состоянияс параллельными спинами фермионов, в частности электронов, зависит от относит. величин этих вкладов. Так, в ферромагнетике (аналогично рассмотренномуатому гелия) более низкой энергией обладает состояние, в к-ром спины (имагн. моменты) электронов в незаполненных оболочках соседних атомов параллельны;в этом случае благодаря О. в. возникает спонтанная намагниченность (см. Ферромагнетизм). Напротив, в молекулах с ковалентной хим. связью, напр. в молекуле Н 2,энергетически выгодно состояние, в к-ром спины валентных электронов соединяющихсяатомов антипараллельны.
О. в. объясняет, т. о., закономерностиатомной и молекулярной спектроскопии, хим. связь в молекулах, ферромагнетизм(и антиферромагнетизм), а также др. специфич. явления в системах одинаковыхчастиц.Лит. см. при ст. Квантовая механики.
Д. А. Киржниц, С. С. Герштейн.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.