Akademik

ПЛАСТИНКИ

ПЛАСТИНКИ: тела, имеющие форму прямой призмы или прямого цилиндра, высота к-рого (толщина) мала по сравнению с размерами основания. По очертанию основания П. делятся на прямоугольные, круглые, эллиптические и т. д. Плоскость, к-рая делит толщину П. пополам, наз. срединной плоскостью.

П. широко применяются в технике как элементы многих конструкций и сооружений; в акустике П. используются в качестве элементов излучателей и приёмников звука, преград в звуковом поле и др.

В зависимости от характера действующих на П. нагрузок различают П., работающие на изгиб при поперечной нагрузке и на растяжение — сжатие при нагрузке, действующей в срединной плоскости.

При деформации изгиба точки П. получают перемещения (прогибы), перпендикулярные к срединной плоскости. Поверхность, к-рую образуют точки срединной плоскости после деформации, наз. срединной поверхностью. В зависимости от характера деформации срединной поверхности при изгибе П. подразделяют на жёсткие, или малого прогиба (не более 1/5 толщины), гибкие (прогиб от 115 до 5 толщин) и абсолютно гибкие, или мембраны (при прогибе св. 5 толщин).

В жёсткой П. без заметной погрешности можно считать её срединный слой при поперечной нагрузке нейтральным, т. е. свободным от напряжений растяжения — сжатия. При расчёте жёстких П. пользуются, как правило, гипотезой прямых нормалей, согласно к-рой любая прямая, нормальная к срединной плоскости до деформации, остаётся и после деформации прямой, нормальной к срединной поверхности, а длина волокна вдоль толщины П. считается неизменной.

В гибкой П. (при расчётах в пределах упругости) наряду с чисто изгибными напряжениями необходимо учитывать напряжения, равномерно распределённые по толщине пластинки. Последние наз. цепными (или мембранными) напряжениями или напряжениями в срединной поверхности. В абсолютно гибкой П., или мембране, при исследовании упругих деформаций можно пренебречь собственно изгибными напряжениями по сравнению с напряжениями в срединной поверхности.

При работе П. под нагрузкой, действующей в срединной плоскости, напряжения распределяются равномерно по толщине, т. е. П. работает в условиях более выгодных, чем в случае поперечной нагрузки. Однако при атом возможна потеря устойчивости П. (см. УСТОЙЧИВОСТЬ УПРУГИХ СИСТЕМ), и её обычно приходится подкреплять сетью рёбер жёсткости.

Важное значение имеет расчёт свободных и вынужденных колебаний П, (т. н. динамич. задачи).

ПЛАСТИНКИ

в акустике - элементыизлучателей и приёмников звука, элементы устройств акустоэлектроники, атакже звуковых преград и перегородок.
П. конечной толщины 2h могут рассматриватьсякак упругий волновод, поле в к-ром является совокупностью волн, наз. нормальнымиволнами. В общем случае произвольной частоты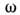 нормальная волна содержит продольную и поперечную компоненты колебат. смещения, распространяющиеся в толще П. и отражающиеся на её границах. Нормальныеволны в П. подразделяются на два класса: Лэмба волны, у к-рых имеютсякак продольные, так и поперечные компоненты колебат. смещения, причём последниенаправлены перпендикулярно плоскости П., и поперечные нормальные волны, обладающие только одной компонентой смещения (отсутствующей в волнах Лэмба),лежащей в плоскости П. и перпендикулярной направлению распространения волны. В П. может распространяться определённое конечное число нормальных волн, отличающихся одна от другой фазовыми и групповыми скоростями, а также распределениямисмещений и напряжений по толщине П. Эти распределения должны удовлетворятьграничным условиям равенства нулю напряжений на обеих плоскостях П.
Число п узловых точек в распределениинапряжений по толщине П. наз. порядком волны. Нормальная волна частоты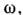 порядка п может распространяться в П. при условии 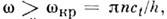где c_t - фазовая скорость поперечной волны в изотропномтвёрдом теле, 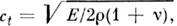Е- модуль Юнга, v - коэф. Пуассона,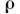- плотность материала П.,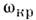- т. н. критич. частота. Число распространяющихся волн тем больше, чембольше значение 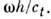Волна заданного порядка п с частотой 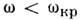не распространяется: в такой волне нет потока энергии, она представляетсобой синфазное движение, экспоненциально спадающее в направлении, параллельномплоскости П.
В тонких П.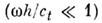возможно распространение только поперечной волны нулевого порядка, смещенияв к-рой по толщине П. одинаковы, а также двух волн Лэмба нулевого порядка, первая из к-рых очень похожа на продольную волну в изотропном твёрдом теле(в ней преобладает продольная компонента смещения), а вторая представляетсобой изгибную волну. При распространении изгибной волны каждыйэлемент тонкой П. смещается перпендикулярно её плоскости. Примерами изгибныхволн в П. являются стоячие волны в деках музыкальных инструментов, в диффузорахгромкоговорителей. Распространяющаяся в тонкой П. изгибная волна малойамплитуды описывается ур-нием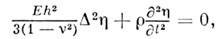

где 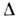- оператор Лапласа,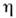- смещение элемента П. от положения равновесия в направлении, перпендикулярномеё плоскости.
Для изгибных волн тонкая П. является системойс дисперсией: волны разл. частот распространяются в ней с разл. фазовымискоростями с _п,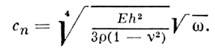

Эта скорость много меньше фазовой скоростипродольных волн в П.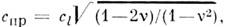где С _l - скорость продольной волны в изотропной сплошнойсреде.
Тонкая П. огранпченного размера обладаетдискретным набором собств. частот, каждой из к-рых соответствует своя формаколебаний, представляющая систему стоячих волн с той или иной картинойузловых линий, разделяющих части П., колеблющиеся с противоположными фазами(см. Хладни фигуры). Собств. частоты и формы колебаний зависят отизгибной жёсткости пластины, равной D = 2Eh³/3(1 - v²),её уд. массы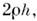 от размеров и формы П., а также от условий закрепления её краёв. Типичнымиусловиями закрепления краёв являются свободный край, шарнирно опёртый край, заделанный край.

Определение спектра собств. частот в общемслучае представляет сложную задачу. Осн. частота может быть определенас помощью метода Рэлея - Ритца. Она составляет, напр., для прямоугольнойшарнирно опёртой П. размером а х b величину

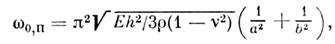
а для круглой П. радиуса а, заделаннойпо краям, величину

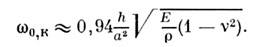
Обертоны осн. частоты круглой П. не являютсягармониками.
Вынужденные колебания П. происходят счастотой внеш. воздействия. При её совпадении с одной из собств. частотимеет место резонанс.
В процессе колебаний П. излучает звукв прилегающую среду при условии, что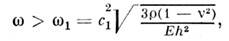

где с₁ - скорость звукав прилегающей среде. При 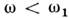в среде возбуждается лишь ближнее поле, экспоненциально спадающее в направлении, перпендикулярном к плоскости П. Излучение звука демпфирует колебания П. и смещает её собств. частоты.
Волновые явления в П. учитываются приопределении звукоизоляции и звуковой прозрачности упругих перегородок. Для описания падения звуковой волны на П. вводят коэф. прохождения плоскойволны через П., равный отношению амплитуды прошедшей и падающей волн. Длянормально падающей волны полностью прозрачна П. толщиной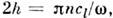 где п= 1,2,3. П. толщиной 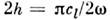является согласующим элементом между средами с волновыми сопротивлениями z₁ и z₂ при условии 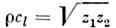(случай"просветления" граппцы раздела сред).

Лит.: Стретт Д ж. В. (лорд Рэлей),Теория звука, пер. с англ., 2 изд., т. 1, М., 1955; Тимошенко С. П., Пластинкии оболочки, пер. с англ., М. - Л., 1948; Морз Ф., Колебания и звук, пер. с англ., М. - Л., 1949; Бреховских Л. М., Волны в слоистых средах, 2 изд.,М., 1973; Викторов И. А., Звуковые поверхностные волны в твёрдых телах, М., 1981; Тимошенко С. П., Янг Д. X., Уивер У., Колебания в инженерномделе, пер. с англ., М., 1985.

С. В. Егерев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.