Akademik

(ее-рассеяние) - процесс, при к-ром два электрона проводимости в металле и полупроводнике переходят из состояний с импульсами (в единицах 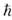)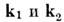в состояние с импульсами 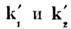в результате кулоновского взаимодействия. При M. р. происходит передача энергии 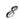и импульса k от одного электрона к другому, но полная энергия и импульс сохраняются: и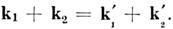

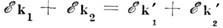
Исключение составляет так называемое M. р. с перебросом, когда

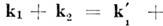
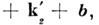где 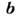- вектор обратной решётки (см. Переброса процессы). В отличие от них процессы с b = 0 наз. нормальными. В полупроводниках и полуметаллах, где 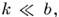M. р. с перебросом обычно запрещено, однако в металлах, где 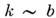, перебросы существенны. Нормальные процессы M. р. устанавливают равновесие внутри электронного газа. Это означает, что любое неравновесное распределение электронов по импульсам 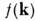, созданное внеш. воздействием, под влиянием M. р. трансформируется в т. н. смещённое фермиевское распределение: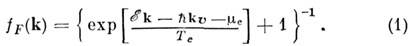

Здесь Т _е и 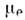- электронная темп-pa и электронный химический потенциал, v- скорость, с к-рой распределение как целое движется относительно кристалла (в системе координат, движущейся со скоростью v,

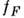- обычное распределение Ферми с 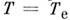). Если

процессы переброса несущественны, то параметры T _е, m_e, v определяются из законов сохранения числа частиц, энергии и импульса.

Распределение (1) устанавливается за время 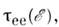в к-рое энергия и импульс перераспределяются между всеми электронами (время релаксации). Для невырожденного электронного газа 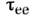определяется соотношением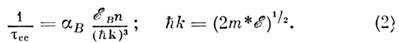

Здесь 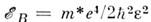- боровская энергия, 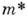- эффективная масса электрона, 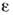- диэлектрич. проницаемость, n- плотность электронов. Для вырожденного электронного газа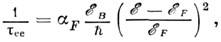

где 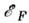- ферми-энергия. Численные множители a_B , 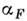засисят от того, какое время релаксации (импульса или энергии), вычисляется.

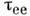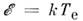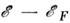
Оценивая время при или = 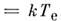, можно найти время установления распределения 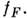Такое распределение устанавливается, только ес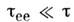ли или 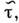где 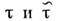- времена релаксации электронов по импульсу и по энергии при рассеянии (на дефектах решётки и фононах).

Роль M. р. в кинетич. явлениях иная, чем у рассеяния на дефектах и фононах. Так как M. р. не изменяет полные импульс и энергию, а только перераспределяет их между электронами, то оно по может быть причиной релаксации импульса и избыточной энергии, к-рые электронный газ получает извне. Поэтому, в частности, M. р. не может обеспечить конечного электросопротивления 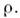Однако оно может изменить сопротивление, обусловленное рассеянием на решётке, напр, "перенося" импульс из области импульсного пространства, где он слабо рслаксирует на дефектах решётки и фононах, в область, где релаксация сильнее. Именно так обстоит дело в случае рассеяния на оптич. фононах с энергией 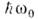при низких темп-pax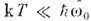, когда рассеяние на решётке является слабым в области 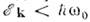и сильным при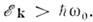

Если узким местом процесса релаксации является именно перенос импульса по -пространству за счёт M. р., то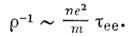

Из этой ф-лы рассеяние на решётке выпадает, но она справедлива, только если 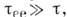и теряет смысл, если рассеяние па решётке полностью "выключить".

M. р. с перебросом не сохраняет полный импульс и тем напоминает рассеяние на решётке. Поэтому оно может быть причиной электросопротивления металла. Оценивая 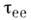при, 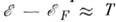получаем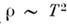

К M. р. относят и столкновения носителей заряда разных типов, напр, электронов проводимости и дырок. Такие процессы приводят к выравниванию их темп-р и хим. потенциалов. M. р. проявляется также в процессах ударной ионизации и рекомбинации (см. Оже-эффект).

Лит.: Гантмахер В. Ф., Левинсон И. Б., Рассеяние носителей тока в металлах и полупроводниках, M., 1084.

И. Б. Левинсон.