Akademik

(от лат. separabu) - траектория динамической системы с двумерным фазовым пространством, стремящаяся к седловому состояниюравновесия при времени 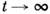(устойчивая С.) или при 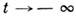(неустойчивая С.). Если С. стремится к седлу при 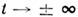,го её (вместе с седлом) называют петлей С. [1, 2]. В диссипативных динамич. системах из петли С. может рождаться предельный цикл[2]. В консервативныхдинамич. системах петли С. могут разделять фазовое пространство наобласти с разл. поведением траекторий. Напр., на фазовом цилиндре (рис.)динамич. системы, описываемой ур-нием маятника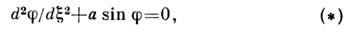

две петли С. отделяют область колебат. движений от области вращат. движениймаятника (см., напр., [3]).Для динамич. систем с размерностью фазовогопространства, большей двух, устойчивые и неустойчивые многообразия седловыхсостояний равновесия и (или) седловых предельных циклов наз. многомернымиС. или сепаратрисными многообразиями. Многомерные С. могут разделять фазовоепространство на области притяжения разл. аттракторов. Связанные с сепаратриснымимногообразиями бифуркации могут приводить к возникновению странныхаттракторов; напр., аттрактор Лоренца рождается в момент, когда неустойчивыеС. седла пересекаются устойчивыми сепаратрисными многообразиями седловыхпредельных циклов.

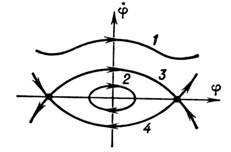
Развёртка фазового цилиндра уравнения (*): траектория, отвечающаяколебательному (1) и вращательному (г) движениям; 3, 4 - сепаратрисы.

Решения, отвечающие С., часто встречаются в разл. физ. приложениях. Они, в частности, описывают класс уединённых волн ( солитонов )внелинейных средах с дисперсией, а также разл. рода доменные стенки, дислокации, дисклинации и др. дефекты в таких средах. Лит.:1) Качественнаятеория динамических систем второго порядка, М., 1966; 2) Теория бифуркацийдинамических систем на плоскости, М., 1967; 3) Рабинович М. И., Т р у бе ц к о в Д. И., Введение в теорию колебаний и волн, М., 1984; 4) БаронеА., Патерно Д., Эффект Джозефсона: физика и применения, пер. с англ., М.,1984. В. С. Афраймович.