- ТРАЕКТОРИЯ
-
(от позднелат. trajectorius — относящийся к перемещению), непрерывная линия, к-рую описывает точка при своём движении. Если Т.— прямая линия, движение точки наз. прямолинейным, в противном случае — криволинейным. Вид Т. свободной материальной точки зависит от действующих на точку сил, нач. условий движения и от того, по отношению к какой системе отсчёта движение рассматривается; для несвободной точки вид Т. зависит ещё от наложенных связей (см. СВЯЗИ МЕХАНИЧЕСКИЕ). Рис. 1. Параболич. траектория.Напр., по отношению к Земле (если пренебречь её суточным вращением) Т. свободной материальной точки, отпущенной без нач. скорости и движущейся под действием силы тяжести, будет прямая линия (вертикаль), а если точке сообщить нач. скорость v0, не направленную вдоль вертикали, то при отсутствии сопротивления воздуха её Т. будет парабола (рис. 1).
Рис. 1. Параболич. траектория.Напр., по отношению к Земле (если пренебречь её суточным вращением) Т. свободной материальной точки, отпущенной без нач. скорости и движущейся под действием силы тяжести, будет прямая линия (вертикаль), а если точке сообщить нач. скорость v0, не направленную вдоль вертикали, то при отсутствии сопротивления воздуха её Т. будет парабола (рис. 1).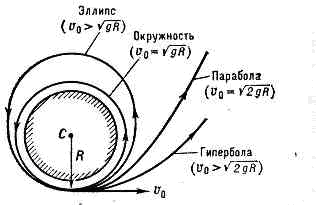 Рис. 2. Виды траекторий в поле тяготения Земли.Т. точки, движущейся в центр. поле тяготения, в зависимости от величины нач. скорости может быть эллипс, парабола или гипербола (в частных случаях — прямая линия или окружность). Так, в поле тяготения Земли, если считать его центральным и пренебречь сопротивлением среды, Т. точки, получившей вблизи поверхности Земли нач. скорость v0, направленную горизонтально (рис._2), будет: окружность, когда v0=?(gR)»7,9 км/с (первая косм. скорость); эллипс, когда ?(2gR) >v0>?(gR); парабола, когда v0=?(2gR)»11,2 км/с (вторая косм. скорость); гипербола, когда v0>?(2gR). Здесь R — радиус Земли, g — ускорение силы тяготения вблизи земной поверхности, а движение рассматривается по отношению к осям, перемещающимся вместе с центром Земли поступательно относительно звёзд; для тела (напр., спутника) всё сказанное относится к Т. его центра тяжести. Если же направление v0 не будет ни горизонтальным, ни вертикальным, то при v0поверхность Земли; таковы Т. центра тяжести баллистич. ракет.Пример несвободной точки — небольшой груз, подвешенный на нити (см. МАЯТНИК). Если нить отклонить от вертикали и отпустить без нач. скорости, то Т. груза будет дугой окружности, а если при этом грузу сообщить нач. скорость, не лежащую в плоскости отклонения нити, то Т. груза могут быть кривые довольно сложного вида, лежащие на поверхности сферы (сферич. маятник), но в частном случае это может быть окружность, лежащая в горизонтальной плоскости (конич. маятник).Т. точек тв. тела зависят от закона движения тела. При поступат. движении тела Т. всех его точек одинаковы, а во всех других случаях движения эти Т. будут вообще разными для разных точек тела. Напр., у колеса автомобиля на прямолинейном участке пути Т. точки обода колеса по отношению к шоссе будет циклоида, а Т. центра колеса — прямая линия. По отношению же к кузову автомобиля Т. точки обода будет окружность, а центр колеса — неподвижен. Определение Т. имеет важное значение как при теор. исследованиях, так и при решении многих практич. задач.
Рис. 2. Виды траекторий в поле тяготения Земли.Т. точки, движущейся в центр. поле тяготения, в зависимости от величины нач. скорости может быть эллипс, парабола или гипербола (в частных случаях — прямая линия или окружность). Так, в поле тяготения Земли, если считать его центральным и пренебречь сопротивлением среды, Т. точки, получившей вблизи поверхности Земли нач. скорость v0, направленную горизонтально (рис._2), будет: окружность, когда v0=?(gR)»7,9 км/с (первая косм. скорость); эллипс, когда ?(2gR) >v0>?(gR); парабола, когда v0=?(2gR)»11,2 км/с (вторая косм. скорость); гипербола, когда v0>?(2gR). Здесь R — радиус Земли, g — ускорение силы тяготения вблизи земной поверхности, а движение рассматривается по отношению к осям, перемещающимся вместе с центром Земли поступательно относительно звёзд; для тела (напр., спутника) всё сказанное относится к Т. его центра тяжести. Если же направление v0 не будет ни горизонтальным, ни вертикальным, то при v0поверхность Земли; таковы Т. центра тяжести баллистич. ракет.Пример несвободной точки — небольшой груз, подвешенный на нити (см. МАЯТНИК). Если нить отклонить от вертикали и отпустить без нач. скорости, то Т. груза будет дугой окружности, а если при этом грузу сообщить нач. скорость, не лежащую в плоскости отклонения нити, то Т. груза могут быть кривые довольно сложного вида, лежащие на поверхности сферы (сферич. маятник), но в частном случае это может быть окружность, лежащая в горизонтальной плоскости (конич. маятник).Т. точек тв. тела зависят от закона движения тела. При поступат. движении тела Т. всех его точек одинаковы, а во всех других случаях движения эти Т. будут вообще разными для разных точек тела. Напр., у колеса автомобиля на прямолинейном участке пути Т. точки обода колеса по отношению к шоссе будет циклоида, а Т. центра колеса — прямая линия. По отношению же к кузову автомобиля Т. точки обода будет окружность, а центр колеса — неподвижен. Определение Т. имеет важное значение как при теор. исследованиях, так и при решении многих практич. задач.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ТРАЕКТОРИЯ
-
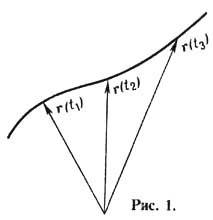
- кривая, к-рую описывает радиус-вектор r(t )координат тела с течением времени (рис. 1). Понятие "Т." тесно связано с понятиями "материальная точка" и "уравнения движения". Говорить о траектории имеет смысл лишь в том случае, когда размеры тела малы по сравнению с расстоянием, к-рое оно проходит.
Для определения ф-ции r(t) (а следовательно, и Т.) необходимо решить дифференц. ур-ние 2-го порядка, вытекающее из 2-го закона Ньютона:
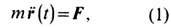
где т - масса тела, F- действующая на него сила.
Ур-ние (1) при заданной F определяет целое семейство траекторий. Выбор к.-л. одной из них осуществляется фиксацией нач. условий, роль к-рых обычно выполняют нач. координаты и скорость тела,
 Напр., подставляя в качестве силы F в ф-лу (1) силу всемирного тяготения,
Напр., подставляя в качестве силы F в ф-лу (1) силу всемирного тяготения,

где G - гравитационная постоянная,
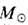 -масса Солнца, т - масса его спутника, n - единичный вектор, направленный от спутника к Солнцу, r- расстояние между ними, и, решая ур-ние (1), можно доказать [И. Ньютон (I. Newton, 1684)], что Т. движения спутника в зависимости от нач. условий является эллипсом, параболой или гиперболой.
-масса Солнца, т - масса его спутника, n - единичный вектор, направленный от спутника к Солнцу, r- расстояние между ними, и, решая ур-ние (1), можно доказать [И. Ньютон (I. Newton, 1684)], что Т. движения спутника в зависимости от нач. условий является эллипсом, параболой или гиперболой.
В классич. механике, если известны координаты и скорость тела в к.-л. момент времени, то Т. движения [ф-ция r(t)]однозначно определяется законом движения (1).
Представление о Т. движения тела как о нек-рой гладкой кривой, к-рую можно найти, решив ур-ние (1), является чисто макроскопическим. Для микроскопич. тел это не так. Из основных постулатов термодинамики следует, что независимо от природы действующих на тело сил среднеквадратичная флуктуация скорости тела, находящегося в термодинамическом равновесии с внеш. средой, описывается ф-лой
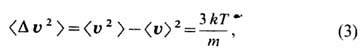
где k- постоянная Больцмана, т - масса тела, Т- абс. темп-pa среды, в к-рую тело помещено.
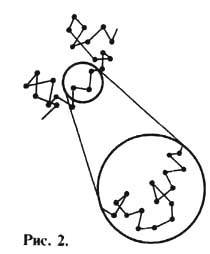
Величина
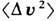 при комнатной темп-ре пренебрежимо мала для макроскопич. тел, но для отд. молекул она составляет уже неск. сотен м в секунду. Поэтому Т. движения микроскопич. тела будет представлять собой хаотическую ломаную линию, подобную изображённой на рис. 2. Это почти везде непрерывная и почти нигде недифференцируемая кривая. Она называется б р о у н о вс к о й т р а е к т о р и е й (см. Броуновское движение )и обладает тем свойством, что если увеличить любой её фрагмент, то мы увидим такую же кривую. Т., изображённая на рис. 2, является случайной, и имеет смысл говорить лишь о статистич. ансамбле таких Т. Полностью определёнными являются только средние по ансамблю величины. Напр., квадрат ср. смещения частицы <x2> как ф-ция времени t есть [А. Эйнштейн (A. Einstein), 1905]:
при комнатной темп-ре пренебрежимо мала для макроскопич. тел, но для отд. молекул она составляет уже неск. сотен м в секунду. Поэтому Т. движения микроскопич. тела будет представлять собой хаотическую ломаную линию, подобную изображённой на рис. 2. Это почти везде непрерывная и почти нигде недифференцируемая кривая. Она называется б р о у н о вс к о й т р а е к т о р и е й (см. Броуновское движение )и обладает тем свойством, что если увеличить любой её фрагмент, то мы увидим такую же кривую. Т., изображённая на рис. 2, является случайной, и имеет смысл говорить лишь о статистич. ансамбле таких Т. Полностью определёнными являются только средние по ансамблю величины. Напр., квадрат ср. смещения частицы <x2> как ф-ция времени t есть [А. Эйнштейн (A. Einstein), 1905]:

где D - коэф. диффузии.
Броуновское движение является заданным, если известна ф-ция

к-рая имеет смысл вероятности того, что частица, находящаяся в точке r1 в момент времени t1 в момент t2 окажется в точке r2.
В простейшем случае одномерного броуновского движения ф-ция (5) имеет вид
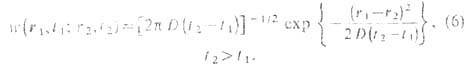
Т. о., для микроскопии, тел Т. является статистич. понятием.
Для квантовых частиц понятие "Т." утрачивает смысл. Количеств. критерием квантового движения является условие

здесь 2p/h - постоянная Планка, т - масса частицы (напр., электрона), u-характерная скорость, L - характерный размер области движения частицы.
"Увидеть" Т. движения квантовой частицы (напр., электрона в атоме) непосредственно при помощи микроскопа или попытаться "поймать" Т. к.-л. способом невозможно. С формальной точки зрения причина состоит в том, что в квантовой частице неприменимо понятие материальной точки, можно говорить лишь об амплитуде вероятности обнаружить частицу в том или ином состоянии. Как показал-Кйзенберг (1927), физ. причина такого положения вещей заключается в том, что, пытаясь измерить положение частицы, мы неизбежно воздействуем на неё, причём это воздействие не может быть меньше постоянной Планка. Следовательно, в квантовом случае [когда выполнено условие (7)] представление о Т. как о геом. месте точек, в каждой из к-рых частицы имеют определ. скорость, физически бессмысленно.
Несмотря на это, в 1947 Т. "вернулась" в квантовую механику благодаря остроумному формализму интегрирования по траекториям, разработанному Р. Фейнманом (R. P. Feynman), и, т. о., легла в основу его интерпретации квантовой механики (см. Фейнмана представление в квантовой механике).
Оказывается, амплитуда перехода квантовой частицы из точки r1,t1 в точку r2,t2 можно записать в виде
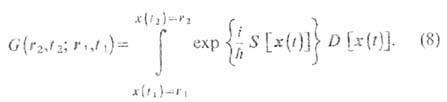
Здесь S[x(t)] -действие классической частицы, движущейся по Т. х(t), символ означает, что необходимо просуммировать величину по всем Т., соединяющим точки r1,t1 и r2,t2. При этом величина
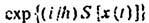 имеет смысл амплитуды вероятности того, что частица попадёт из точки r1,t1 в точку r2,t2, двигаясь по Т. x(t). Т. о., суммируя амплитуды вероятности переходов по всевозможным Т., мы получим амплитуду пере хода G квантовой частицы (рис. 3).
имеет смысл амплитуды вероятности того, что частица попадёт из точки r1,t1 в точку r2,t2, двигаясь по Т. x(t). Т. о., суммируя амплитуды вероятности переходов по всевозможным Т., мы получим амплитуду пере хода G квантовой частицы (рис. 3).
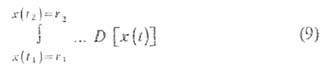
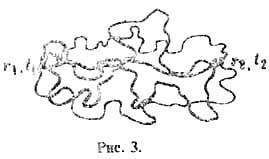
Ур-ние (1) определяет экстремальную Т. в интеграле (8), к-рую называют классич. Т.
В классич. механике, к-рая описывает поведение мак-роскопич. тел, Т. движения является непосредственно измеряемой величиной. Для микроскопич. тел имеет смысл говорить лишь о статистическом ансамбле траекторий, поскольку для таких тел существенную роль играют термодинамич. флуктуации. И, наконец, в квантовой области представление о Т. как .о наблюдаемой физ. величине не имеет смысла. И всё же Т., уже как матсм. абстракция, образует основу очень красивого и плодотворного описания природы на квантовом уровне.
Лит.: Винер Н., Нелинейные задачи в теории случайных процессов, пер. с англ., М., 1961; Фейнман Р. Ф., Хибс А. Р., Квантовая механика и интегралы по траекториям, пер. с англ., М., 1968; Сивухин Д. В., Общий курс физики, 3 изд., т. 1. Механика, М., 1989. М. А. Савров.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.