Akademik

К энергетически изолированным от окружающей среды системам с энергией 8 при пост. объёме V и с заданным числом ч-ц N (микроканонический ансамбль Гиббса) применимо микроканонич. распределение Гиббса

f(p,q)=Ad{H(p,q)-?},

где d — дельта-функция Дирака, А — постоянная, позволяющая определить энтропию системы как ф-цию ?, V, N.

Системы в контакте с термостатом, т. е. с перем. энергией, имеющие пост. объём и заданное число ч-ц (канонический ансамбль Гиббса), описываются канонич. распределением Гиббса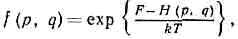

где F — свободная энергия (Гельмгольца энергия) как ф-ция V, Т, N.

Системы, имеющие пост. объём, при термич. и матер. контакте с термостатом (т. н. Гиббса большой канонический ансамбль) обладают перем. энергией и перем. числом ч-ц (за счёт обмена с термостатом энергией и в-вом) и описываются большим канонич. распределением Гиббса

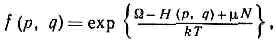где m, — химический потенциал, W — термодинамич. потенциал в переменных V, Т, m.

Системы в термич. и механич. контакте с окружающей средой, т. е. с переменными энергией и объёмом, но пост. давлением р (изобарически-изотермич. ансамбль Гиббса), описываются изобарич. Г. р.

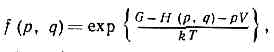где G — Гиббса энергия.

Для квант. систем Г. р. имеют такую же форму, но вместо Н(р, q) в них стоит энергия квант. уровня системы ?i. Из условия, что полная вероятность пребывания системы в к.-л. из состояний равна единице (условие нормировки), определяются константы A, F, W, G в Г. р., т. е. все потенциалы термодинамические (см. СТАТИСТИЧЕСКАЯ ФИЗИКА). Для вычисления термодинамич. ф-ций можно пользоваться любым Г. р., они в этом случае эквивалентны, несмотря на то что каждое Г. р. соответствует определ. физ. условиям.