Akademik

PHONON

Les phonons, ou vibrations collectives d’un ensemble d’atomes en interactions, représentent un des aspects les plus importants de la physique des solides. Ils interviennent dans des propriétés aussi diverses que la propagation d’ondes sonores, la chaleur spécifique, la conductivité thermique et électrique, la supraconductivité, la ferro-électricité. On peut comprendre l’existence de telles vibrations à partir des interactions de chaque atome avec ses voisins: si on impose localement, à la surface par exemple, un mouvement perturbateur qui déplace un certain nombre d’atomes de leur position d’équilibre, ceux-ci agissent sur leurs voisins, et la perturbation locale de départ s’étend de proche en proche au solide tout entier sous forme d’un mouvement collectif. Dans l’approximation classique où l’on assimile le solide à un continuum élastique, on peut montrer que le mouvement le plus général est la superposition d’ondes progressives de la forme:

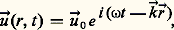
où ゎ⁰ est l’amplitude de la déformation, 益 = 諸/2 神 la fréquence de vibration, = 2 神/k la longueur d’onde et v = 諸/k la vitesse de phase de l’onde. Celle-ci est indépendante de la fréquence; en revanche, elle dépend de l’orientation de ゎ⁰ par rapport au vecteur d’onde や. Mais on sait que, à l’échelle des atomes, il faut remplacer la mécanique classique par la mécanique quantique; celle-ci implique une quantification de l’énergie 﨎^k de l’onde, c’està-dire 﨎^k = (n^k + 1/2) 寮 諸^k , où n^k est un nombre entier et 寮 la constante de Planck. On peut aussi définir une impulsion ら du cristal, quantifiée en unités de 寮 k. Tout cela permet d’introduire le langage corpusculaire, qui assimile une onde à un ensemble de n^k quasiparticules, ou phonons d’énergie 寮 諸^k et d’impulsion 寮 や.

Nature des phonons

Modes de vibrations acoustiques et optiques

Il est instructif d’analyser d’abord les modes de vibration de chaînes unidimensionnelles d’atomes. Nous allons considérer deux cas: d’une part, une chaîne d’atomes de masse M positionnés en xⁿ = na ; d’autre part, une chaîne moléculaire avec des molécules M² formées de deux atomes identiques positionnés en xⁿ = na et na + d (avec d 麗 a /2) [fig. 1]. On admettra, dans ce second cas, qu’il y a à la fois des forces intramoléculaires et intermoléculaires.

Chaque atome vibre autour de sa position d’équilibre dans le puits de potentiel créé par ses voisins: ce potentiel est parabolique pour les mouvements de faible amplitude, c’est-à-dire que les forces interatomiques sont assimilées à des ressorts de constante 見¹ (dans le premier cas), et 見¹ et 見² (dans le second cas). On dit que l’on est dans l’«approximation harmonique». Si on cherche des solutions de la forme uⁿ (t ) 黎 e^{i (} size=1^諸t size=1^{漣kna )} (avec r = na ), on peut montrer qu’elles peuvent être représentées par des courbes de dispersion 諸(k ) qui donnent les fréquences de vibration permises pour un vecteur d’onde k donné. Dans le premier cas, on obtient ainsi une seule courbe de dispersion (fig. 1 a), qui est linéaire ( 諸 = vk ) au voisinage de k = 0; cela justifie le nom de «branche acoustique» donné à cette courbe. Remarquons également qu’il existe une fréquence de vibration maximale pour k = 梁 神/a .

Pour le second cas (fig. 1 b), on obtient deux branches: une branche acoustique et une branche optique ; 諸 dépend peu de k pour cette dernière branche et sa valeur est, en première approximation, égale à la fréquence de vibration de la molécule M²; cette dernière valeur est un peu élargie par les couplages intermoléculaires. Signalons qu’une différence de masse entre les deux atomes de la molécule conduit également à un élargissement de la branche optique. La figure 1 montre également les amplitudes de vibration lorsque k est voisin de 0: on remarque surtout que les vibrations sont en opposition de phase pour les deux atomes d’une même molécule. C’est de là que vient l’appellation «optique» pour cette branche: de telles vibrations sont facilement excitées par le champ électrique de la lumière si les deux masses portent des charges opposées, comme c’est le cas dans les cristaux ioniques.

Dans le cas général à trois dimensions et avec r atomes par maille élémentaire, on peut montrer qu’il y a 3r branches de phonons: 3 branches acoustiques, dont deux sont essentiellement transverses ( ゎ⁰ 旅 や) et une longitudinale ( ゎ⁰// や), et 3(r 漣 1) branches optiques. Les valeurs physiquement significatives sont contenues dans la première zone, dite de «Brillouin» (entre 梁 神/a pour la fig. 1) [cf. physique des SOLIDES], et le nombre de vibrations indépendantes est égal à 3r N, où N est le nombre de mailles élémentaires dans le solide.

L’existence d’un nombre fini, quoique considérable, de modes de vibration est liée aux limites imposées aux mouvements des atomes à la surface du solide.

Détermination des courbes de dispersion size=4諸(k)

Pour déterminer les courbes de dispersion, on fait interagir le cristal avec un rayonnement externe (rayons X, lumière, neutrons). Les neutrons, par exemple, voient le cristal et ses mouvements, par l’intermédiaire de leurs interactions avec le noyau; au cours de l’interaction, le neutron ou le photon peut absorber (ou émettre) un phonon: on dit que la particule incidente est diffusée inélastiquement. Le vecteur d’onde de la particule incidente change de ら en ら et son énergie de E en E , de telle manière que:

Remarquons que la quantité de mouvement n’est conservée qu’à un vecteur て du réseau réciproque près (cf. physique des SOLIDES): cela résulte de la symétrie de translation du cristal. On peut remonter aux courbes de dispersion en mesurant les angles de diffusion (fig. 2 a) et l’énergie des particules diffusées. Cette méthode est particulièrement puissante dans le cas des neutrons, qui peuvent avoir à la fois des vecteurs d’onde et des énergies adaptés à ceux des phonons, sur toute la gamme des valeurs de 諸 et k . En revanche, la résolution est moindre dans le cas des rayons X et de la lumière.

Pour la lumière, on parle de «diffusion Raman» quand les phonons sont optiques, et de «diffusion Brillouin» quand ils sont acoustiques.

Aspects thermodynamiques

Vibrations thermiques

Les vibrations internes à un solide peuvent également être excitées par la température T. L’agitation thermique qui en résulte est la superposition plus ou moins chaotique d’un grand nombre de vibrations, couvrant pratiquement tout le spectre des fréquences. Toutes ces vibrations sont indépendantes les unes des autres dans l’approximation harmonique, et on peut les assimiler à un gaz de phonons libres. La contribution d’un mode particulier à l’énergie thermique est alors égale à 讀^k 練 寮 諸^k , où 讀^k est le nombre de phonons de vecteur d’onde や. Ce nombre fluctue, mais sa valeur à l’équilibre thermique correspond à une statistique de Bose-Einstein avec:

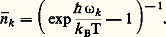
Capacité thermique

La chaleur spécifique C^v est alors donnée par:

On distingue deux domaines de température, suivant que celle-ci est plus grande ou plus petite que ^D, la température de Debye. ^D caractérise la valeur maximale 諸^m des énergies des vibrations, c’est-à-dire k ^{B D} 力 寮 諸^m . Si T 礪 ^D, on a:

(loi de Dulong et Petit, si r = 1).

Si T 麗 ^D, on trouve:

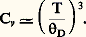
Le fait que C^v tende progressivement vers zéro aux basses températures résulte de l’impossibilité, pour l’énergie thermique, d’exciter les modes pour lesquels k ^BT 麗 寮 諸; ces modes ne participent plus à l’énergie thermique. On peut remarquer aussi que U(T) 黎 ⁴, si T 麗麗 ^D. Ce résultat est tout à fait analogue à l’énergie thermique d’un gaz de photons (rayonnement de corps noir).

Propriétés de transport et phonons

Anharmonicité, dilatation et conductivité thermique

L’approximation d’oscillations harmoniques utilisée jusque-là ne permet pas d’expliquer un certain nombre de phénomènes aussi généraux que la variation des fréquences de vibration avec la pression, l’existence d’une dilatation thermique, la valeur finie de la conductibilité thermique d’un cristal isolant électrique. L’inclusion de termes non quadratiques dans le potentiel interatomique conduit non seulement à une valeur finie de la dilatation variant avec la température, comme C^v , mais aussi à des interactions phonon-phonon. Deux phonons や¹ et や² peuvent par exemple interagir pour former un troisième phonon や³ (fig. 2 b): ces collisions entre phonons définissent un libre parcours moyen l (T) entre collisions successives qui intervient dans le coefficient de

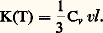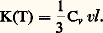conductivité thermique Ces

chocs seraient cependant sans effet sur un courant de chaleur si la quantité de mouvement était strictement conservée lors de l’interaction: mais nous savons que cette conservation n’est effective qu’à un vecteur て du réseau réciproque près (processus umklapp, fig. 2 b). À haute température, l (T) varie comme 1/T en relation avec la densité croissante de phonons; à basse température, l (T) tend en principe vers l’infini, mais la présence de défauts limite généralement sa valeur à une constante indépendante de T.

Couplage électron-phonon dans les métaux

Les électrons de conduction d’un métal interagissent avec le potentiel électrostatique des ions, mais il est bien connu que le mouvement des électrons reste libre tant que ce potentiel est périodique. La présence de vibrations détruit cette périodicité et conduit à une diffusion des électrons par les phonons (fig. 2 a): la conductivité électrique 靖 varie de ce fait en 1/T à suffisamment haute température, tout comme la conductivité thermique et, comme cette dernière, elle est limitée par la présence d’impuretés à basse température. Plus spectaculaire encore est le phénomène de supraconductivité, avec la brusque disparition de toute résistivité électrique 福 = 1/ 靖 en dessous d’une température critique T^c : on sait maintenant que cette transition est due à des interactions attractives entre paires d’électrons de conduction liées à l’émission de phonons par l’un des électrons et à leur absorption par l’autre (fig. 2 c).

Instabilités liées aux phonons

Instabilités structurales

De nombreux composés métalliques ou ioniques présentent des transitions structurales; en général, il s’agit d’un abaissement de la symétrie cristalline en dessous d’une température critique T^c . Il peut provenir soit d’un déplacement d’atomes à l’intérieur de la maille élémentaire (cas des perovskites Ba Ti³, Sr Ti³, etc.), soit d’une déformation élastique de la maille qui affecte la géométrie de celle-ci (cas de Nb³Sn, de TmV⁴), soit d’une modulation sinusoïdale du paramètre de la maille (métaux organiques quasiunidimensionnels, NbSe²), soit d’une transition ordre-désordre quand certains groupements atomiques possèdent deux positions d’équilibre (phosphate KH²P⁴, NH⁴Br, etc.). Toutes ces transitions sont accompagnées d’une diminution des fréquences de vibration de certains modes qui peuvent même s’annuler à T^c si la transition est du deuxième ordre (fig. 3). L’origine de ces instabilités, ou modes mous , est diverse; dans les métaux, elle est liée à l’écrantage des forces ions-ions par les électrons de conduction: cet effet est particulièrement prononcé dans les métaux de basse dimensionnalité et pour des vecteurs d’ondes や qui joignent des régions à grande densité d’états de la surface de Fermi (cf. physique des SOLIDES); dans les cristaux ioniques, elle est liée à la compensation entre forces répulsives à courte portée et forces attractives à longue portée, induites par la polarisation diélectrique: le degré de compensation peut dépendre de la température par l’intermédiaire d’effets anharmoniques; l’effet Jahn-Teller coopératif est une autre possibilité: le changement de symétrie lève la dégénérescence de certains niveaux électroniques et abaisse l’énergie du système. Toutes ces transitions de phase sont très étudiées car elles sont fondamentales pour la compréhension de phénomènes aussi divers que la ferro-électricité, la transition métal-isolant, l’optimisation des propriétés supraconductrices...

Fusion

Le rôle des phonons dans le phénomène de fusion est attesté par l’étroite corrélation qu’il y a entre les températures de fusion T^f et l’amplitude des vibrations atomiques. Qualitativement, on constate qu’un solide fond quand le carré moyen des amplitudes de vibration dépasse une fraction empirique de la distance interatomique (critère de Lindemann). Il existe de même des corrélations entre les valeurs de T^f et le coefficient de dilatation thermique. La transition solide-liquide reste cependant mal comprise à ce jour, du fait de notre mauvaise connaissance de l’état liquide. On peut montrer, cependant, qu’il n’existe plus de phonons transverses dans un solide au-dessus d’une température critique, si on admet que la force qui agit sur un atome résulte d’une moyenne thermodynamique sur l’ensemble des configurations atomiques. Cette instabilité annonce peut-être l’état liquide, qui est précisément caractérisé par l’absence de modes acoustiques transverses.

• v. 1965; de phon(o)-, d'apr. photon

n. m. PHYS Quantum d'énergie du champ d'agitation thermique des noyaux. (Il transporte l'énergie hf, h étant la constante de Planck et f la fréquence d'oscillation.)

⇒PHONON, subst. masc.

PHYS. ,,Particule fictive correspondant en mécanique quantique à l'excitation d'un mode de vibration dans un cristal, ou d'une onde de compression dans un liquide`` (Nucl. 1975). La quantification des ondes d'agitation thermique a donné naissance au concept de «phonon» (Hist. gén. sc., t.3, vol. 2, 1964, p.247).

Prononc.:[]. Étymol. et Hist. 1964 (Hist. gén. sc., loc. cit.). Formé de l'élém. phon(o)- et du suff. -on².

phonon [fɔnɔ̃] n. m.

ÉTYM. V. 1965; de phon-, et suff. -on, sur le modèle de photon.

❖

♦ Phys. Quantum d'oscillation d'une particule dans un réseau cristallin. || « Cette énergie (des électrons de valence interagissant avec un réseau cristallin) contribue à exciter les vibrations de noyaux ou phonons qui se propagent suivant la périodicité du réseau » (la Recherche, juin 1980, p. 716).