Akademik

PROGRAMMATION

Un ordinateur est une machine universelle pour le traitement de l’information. Il doit pouvoir être utilisé aussi bien pour des calculs numériques que pour la gestion d’un stock de pièces détachées ou des travaux de secrétariat. Il est donc construit pour exécuter les fonctions primitives de ces traitements: additionner, soustraire, multiplier, diviser, comparer des nombres, mais aussi mettre bout à bout des caractères alphabétiques, les comparer, couper en morceaux des suites de lettres, etc. On obtient un traitement complexe en combinant ces opérations entre elles dans un ordre convenable. Mais, la vitesse de l’ordinateur étant très grande, il n’est pas possible de lui donner des ordres à mesure de l’avancement du travail, comme on le fait avec une calculette: il faut dresser d’abord la liste des instructions auxquelles la machine devra obéir, dans l’ordre de leur exécution, ce qu’on appelle un programme d’ordinateur . On le charge dans la mémoire de la machine, où elle puisera les instructions à mesure de leur exécution, à sa propre vitesse.

Si l’on veut faire exécuter une tâche à la machine ou si on veut lui faire résoudre un problème, il faut donc rédiger le programme correspondant, c’est-à-dire avoir trouvé quelle suite d’opérations élémentaires assure l’exécution de la tâche ou la résolution du problème dans tous les cas à envisager. En un mot, il faut trouver une méthode d’exécution de la tâche ou de résolution du problème, aussi appelée algorithme . Ce n’est pas toujours facile: il ne suffit pas d’être capable d’exécuter une tâche pour pouvoir décrire la méthode par laquelle on l’exécute, car nos actions sont rarement méthodiques. Nous pouvons tous mettre un paquet de fiches en ordre alphabétique: rares sont ceux qui utilisent pour cela une méthode systématique et qui sont capables de l’expliciter. Il y a une grande distance entre savoir faire et pouvoir faire faire par une machine. Il faut bien définir quelles sont les données du travail, quelles circonstances variées peuvent se produire, quelles actions sont à prendre dans chaque cas pour parvenir au résultat recherché.

Certains disent que ce travail proprement algorithmique n’est pas l’affaire du programmeur, dont la seule tâche est de rédiger le résultat de cette analyse dans un langage acceptable par un ordinateur. La programmation est alors pure affaire de codage, ne demandant que peu de compétence. Cette division du travail n’a plus de sens aujourd’hui: les langages de programmation sont suffisamment évolués pour que leur apprentissage soit simple. En rédigeant lui-même son programme, l’analyste évite beaucoup d’erreurs de communication avec le programmeur: imprécision et ambiguïté des consignes, oubli de cas particuliers dans l’analyse que la programmation fait apparaître, etc. Connaissant bien son programme, il est à même de le modifier si quelque particularité apparaît qu’il n’avait pas envisagée.

La programmation s’est d’abord faite de façon empirique: on rédige un programme approximatif, on le met en œuvre sur ordinateur pour en faire apparaître les déficiences, que l’on corrige ou pallie de façon plus ou moins fiable. On ne connaissait pas à l’époque d’autre méthode de travail. Il est apparu, vers la fin des années 1960, que cette façon de faire était très mauvaise, produisant des programmes dont on n’est jamais certain qu’ils soient corrects, et qui peuvent se révéler très dangereux aussi bien pour des applications industrielles (pilotage de processus chimiques...) que de gestion (comptabilité dans une banque...). Un programme doit être juste par construction, et non pas parce que pour le moment on a pu corriger toutes les erreurs qui se sont manifestées. La preuve de la validité d’un programme est de la responsabilité de son concepteur, et la théorie a fourni les moyens de telles preuves.

La programmation est ainsi devenue une œuvre intellectuelle exigeante et, partant, longue et onéreuse. On a donc imaginé d’en contourner la nécessité par des logiciels spécialisés, qui permettent de faire exécuter par l’ordinateur des fonctions propres à certains domaines d’activité: gestion de fichiers, travaux sur des tableaux de nombres, création et mise en forme de textes, gestion d’images, travaux de facturation, rédaction d’actes, etc. Ces fonctions étant très complexes et d’exécution relativement lente, il n’est pas alors absurde de les commander une par une, suivant l’évolution d’une tâche. Il n’est plus nécessaire de prévoir ce qui peut se passer; il suffit de constater ce qui s’est réellement produit. N’importe qui peut utiliser, sans savoir programmer, un ordinateur transformé en calculette pour tableaux ou fichiers. D’où la prédiction de certains que la programmation deviendra une activité réservée à un petit nombre de spécialistes, et qu’il est donc inutile de la connaître.

Il s’agit d’un grave contresens. Si l’on ne sait pas sur quoi reposent les outils que l’on utilise, on perd tout esprit critique à leur égard. On utilise mal des outils dont on ne comprend pas pourquoi ils sont ainsi, ne sachant pas si leurs limitations viennent de la nature même des traitements qu’ils effectuent ou de la faiblesse des réalisateurs. Au lieu d’avoir des machines à son service, on en devient les servants. Programmer, c’est vraiment prendre une tâche en charge, de sa première formulation jusqu’à son exécution par la machine. C’est le cœur même de l’informatique. On ne peut comprendre ce qu’est cette science si l’on n’a aucune idée de l’activité de programmation: aucune tâche ne peut être faite par une machine qu’on n’en ait d’abord trouvé une méthode d’exécution, et qu’on ne l’ait exprimée dans un langage qui lui soit accessible.

La programmation demande de la créativité, pour imaginer la méthode infaillible qui conduira dans tous les cas des données au résultat. Elle demande de la rigueur: dans l’analyse, pour être certain d’avoir mis en évidence toutes les éventualités; dans la liste des actions à prendre, pour être sûr d’avance qu’elles produiront les bons résultats. Elle exige la clarté de l’expression, enfin, parce qu’un programme est d’abord écrit pour être lu par un homme: il évolue dans le temps, à mesure des besoins des utilisateurs et des possibilités des ordinateurs. Par là, la programmation s’inscrit dans le cadre des grandes activités intellectuelles de l’homme. Elle fait partie du patrimoine culturel de la fin du XX^e siècle.

Les langages de programmation

Tel qu’il est enregistré dans la mémoire d’un ordinateur, un programme est une suite de 0 et de 1, rédigée suivant des règles précises que l’on peut assimiler à des règles de grammaire, définissant un certain langage appelé langage de la machine . Il est impraticable par l’homme, parce que trop difficile à déchiffrer. On a donc imaginé de créer des langages dits évolués, écrits avec l’alphabet usuel, comportant des sigles ayant une valeur mnémotechnique pour l’utilisateur. Pour chaque langage et chaque type de machine, on a rédigé un programme (baptisé compilateur) qui assure la traduction de tout texte écrit avec le langage évolué en un texte en langage de la machine, en garantissant la fidélité de la traduction: les actions exécutées par la machine sont effectivement celles qui sont décrites par le langage évolué.

Un langage de programmation n’est pas n’importe quelle variante d’un langage ordinaire. Il ne peut souffrir l’ambiguïté; il ne doit offrir aucune latitude d’interprétation. Le premier langage évolué fut Fortran, inventé par John Backhus en 1955. On a du mal à se représenter aujourd’hui la complexité de cette invention: il fallut reconnaître le champ sémantique que devait couvrir le langage, inventer une grammaire qui élimine toute ambiguïté, toute polysémie. Il fallut trouver des algorithmes de traduction qui garantissent la conservation des opérations désignées dans le langage évolué. Il fallut, à l’époque, que le premier compilateur soit performant, pour ne pas freiner l’usage de Fortran.

Ce premier pas franchi, les voies de la compilation étant ouvertes, créer un nouveau langage était beaucoup plus simple. Il en parut plus de quatre mille! Les linguistes s’interrogent sur les raisons qui ont pu pousser l’humanité à la dispersion des langues. Nous avons vu se répéter sous nos yeux, en quelques décennies, une nouvelle Babel. Il serait sans doute instructif d’en étudier la genèse. Les effets en ont été pervers: pendant qu’on dépensait une énergie fantastique à inventer des langages et à en écrire des compilateurs, on n’avait guère le temps de réfléchir à l’essentiel. «Ce que l’on conçoit bien s’énonce clairement, et les mots pour le dire arrivent aisément.» Le problème de la programmation n’était pas le langage, mais la pensée algorithmique. Il a fallu un ralentissement dans la création des langages, vers la fin des années 1960, pour qu’enfin s’élabore une théorie de la programmation.

La production de nouveaux langages s’est considérablement ralentie. On peut classer les langages en quatre grandes familles, qui correspondent à quatre formes de pensée différentes. À l’intérieur d’une famille, les langages diffèrent par leur plus ou moins grande sévérité syntaxique, par la richesse des constructions qu’ils permettent ou des fonctions qu’ils offrent, par la variété des objets qu’ils permettent de manipuler. Mais on passe assez facilement d’un langage à l’autre.

La programmation impérative

Les langages impératifs ne s’éloignent des langages machines que par leur richesse d’expression; ils en gardent la structure de calcul. À la base, il y a le fait qu’un ordinateur est construit autour d’une mémoire divisée en cases dans lesquelles on peut ranger des informations. On peut consulter le contenu d’une case, ce qui ne le modifie pas, on peut placer un contenu dans une case en détruisant automatiquement le précédent. Le concept de case se retrouve dans celui de variable d’un langage de programmation impératif, désignée par un nom, X par exemple, dont on peut connaître la valeur:

fera afficher la valeur de X sur l’écran de l’ordinateur. On peut affecter une valeur à une variable:

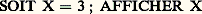
donne à la variable X la valeur 3, puis l’affiche sur l’écran.

L’instruction

(où IS doit être considéré comme une parenthèse fermante associée à la parenthèse ouvrante qu’est le mot SI) est dite conditionnelle et fait afficher X s’il est plus grand que 0; sinon, 0. L’instruction d’affectation permet de donner une valeur à une variable, mais aussi de la changer:

consulte la valeur de X (ici 3), lui ajoute 1 et donne le résultat comme nouvelle valeur à X. X prend ainsi la valeur 4. Tout cela paraît fort simple. Malheureusement, ces écritures décrivent un processus évolutif par lequel il devient difficile de suivre l’effet d’une suite d’instructions: il y a la valeur de X avant l’exécution d’une instruction, et sa valeur après, qui peut ne pas être la même. Une simple lecture ne permet pas de dire ce que fait le morceau de programme que voici:

Un programme décrit une suite d’actions, qui fait passer de la situation initiale (celle des données) à la situation finale (celle des résultats). Pour en connaître l’effet, il faut détailler la suite de situations qui est engendrée par la suite d’actions. Supposons qu’au début X ait la valeur a et Y la valeur b :

Nous voyons que les valeurs de X et Y ont été échangées. La programmation impérative repose sur le couple situation-action. Le programme décrit la suite d’actions qui fait passer de la situation initiale à la situation finale. Pour établir la validité d’un programme, on détermine (comme nous venons de le faire dans un exemple simple) la suite de situations qu’il engendre. Si, pour toutes les données possibles, la situation finale est celle que l’on attend, le programme est juste.

Mais il est maladroit d’écrire d’abord un programme, puis de faire un travail de preuve, qui devient très complexe dès que se multiplient les instructions conditionnelles. Il faut fonder la construction du programme sur la connaissance que l’on a des situations initiale et finale. Si elles sont suffisamment proches l’une de l’autre, les actions à prendre pour passer de l’une à l’autre sont évidentes, et le programme vite écrit. Si ce n’est pas le cas, il faut imaginer des situations intermédiaires, de façon que le passage de l’une à l’autre soit évident.

Supposons, par exemple, qu’il faille justifier un texte à droite, c’est-à-dire obtenir une marge rectiligne à droite. Pour simplifier, supposons encore que l’on ne cherche pas à modifier le contenu de chaque ligne, mais que l’on joue seulement sur les caractères «espace». Il faut mettre autant de ces caractères qu’il est nécessaire entre les mots pour que toutes les lignes aient la même longueur sans «espace» à droite. Dans la situation initiale, la ligne est une suite de mots, sans «espace» au début ni à la fin, les mots étant séparés par des espaces. Dans la situation finale, le nombre d’espaces entre les mots a changé, il n’y en a toujours pas au début ni à la fin, et la longueur de la ligne est égale à une valeur donnée d’avance. Ce qui change entre la situation initiale et la situation finale, c’est que le nombre total de caractères «espace» a augmenté (si la ligne initiale est trop courte), et qu’ils sont répartis aussi régulièrement que possible entre les mots.

Pour y parvenir, il faut connaître le nombre p d’espaces dans la ligne initiale, le nombre k d’espaces à ajouter pour atteindre la bonne longueur et, enfin, le nombre i d’intervalles dans lesquels répartir ces signes. La division du nombre d’espaces p + k par le nombre d’intervalles i donnera un quotient q et un reste r . On mettra q + 1 espaces dans les r premiers intervalles, q dans les autres. On a ainsi décomposé le problème en problèmes plus petits: compter le nombre d’espaces dans la ligne donnée, le nombre d’espaces à ajouter, le nombre d’intervalles, faire une division, réécrire la ligne en mettant le nombre d’espaces ainsi trouvé entre les mots. Cette façon de programmer a été appelée programmation descendante , simple application à l’informatique de la méthode de Descartes.

Il arrive qu’un problème ne se laisse pas décomposer en problèmes plus petits. Supposons que l’on veuille mettre en ordre croissant une suite de nombres. On ne voit aucune façon de décomposer ce problème en sous-problèmes. On va alors essayer de le résoudre de proche en proche. Supposons que l’on ait pu trouver les derniers nombres de la suite (les plus grands) et les mettre en bon ordre au bout de la suite. On est parti de la suite:

et on a mis les trois plus grands au bout:

Ils sont ordonnés, à leur place définitive. Comment avancer? Caractérisons d’abord la situation atteinte. Il y a au bout une partie triée, en place. Le début est en désordre. Il faut réduire la longueur de la partie en désordre et étendre la partie triée en place. Quel élément lui ajouter? Le plus grand élément de la première partie. Il faut donc chercher le plus grand élément de la première partie de la liste et l’amener au bout de cette partie. La partie en désordre perd un élément, la partie triée au bout en gagne un. Quand il n’y aura plus qu’un élément dans la partie en désordre, il n’y aura plus de désordre; ce sera fini.

Pour préciser un peu, appelons n le nombre d’éléments de la liste à trier, m le nombre d’éléments de la partie en désordre (rang de son dernier élément à droite). Au début, tout est en désordre: m = n . Quand on a réussi à mettre en place un élément de la partie en désordre, sa longueur diminue de une unité, ce qui s’écrit:

On obtient le programme suivant:

Les actions entre FAIRE et BOUCLER sont répétées tant que la condition m 礪 1 est vraie. Les deux actions décrites en français courant devront être mises sous la forme de programme, mais elles sont plus simples. Pour trouver la place du plus grand élément entre 1 et m , on supposera qu’on a trouvé la place k du plus grand entre 1 et p . Si p = m , c’est fini. Sinon, si l’élément en p est plus grand que celui en k , c’est lui le plus grand. On augmente p de une unité. L’échange des éléments en k et m peut être fait comme on l’a vu plus haut, ou par d’autres méthodes.

Il faut bien comprendre l’esprit de cette méthode. Le point de départ est la proposition d’une situation intermédiaire: «Supposons que j’ai pu faire une partie du travail, donnant la situation que voici.» C’est ce qu’en mathématique on appelle une hypothèse de récurrence. On cherche alors comment passer d’un cas au suivant, puis comment démarrer, c’est-à-dire atteindre une première fois, sans trop de travail, la situation de récurrence. La récurrence est le fondement de la programmation impérative. La créativité s’exerce dans le choix d’une hypothèse, choix que l’on peut modifier ou retoucher s’il s’avère qu’il était mal venu. Le programme étant construit à partir des situations qu’il engendre, on sait qu’il fournira le bon résultat.

La programmation par objets

La programmation impérative donne la liste d’actions à faire sur les objets usuels: nombres, caractères, etc. Les applications nombreuses de l’informatique ont élargi les domaines d’application. Un progiciel utilise des moyens de communication variés (une «souris» par exemple), gère des fenêtres sur l’écran. Si des ordinateurs sont connectés en réseau, certains objets peuvent être accessibles par plusieurs utilisateurs qui les consultent ou les modifient, ce qui pose de délicats problèmes de gestion des ressources. Une nouvelle approche de la programmation a donc été créée, qui met au premier plan les objets du traitement. Un utilisateur définit des classes d’objets, caractérisés par leur structure et par les actions que l’on peut faire sur eux. On peut alors créer une instance d’un objet de la classe, et exécuter sur lui les traitements qui ont été définis pour cette classe. Une sous-classe peut être définie dans une classe; elle hérite alors des propriétés de cette classe. Les objets peuvent être propres à un utilisateur, ou partagés entre plusieurs.

Imaginons qu’un dispositif périphérique onéreux soit connecté à un réseau d’ordinateurs (par exemple une table à dessin en couleurs). Pour en faciliter l’utilisation, il est demandé à chaque utilisateur de s’inscrire dans un planning. L’objet «planning» est constitué de tranches de temps réparties dans la semaine. On peut consulter une case pour savoir si elle est libre; on peut retenir une case libre. Les cases disparaissent du planning avec l’avancement du temps. Certaines opérations sont délicates: un utilisateur peut consulter une case au moment même où un autre est en train de la retenir; il faut que l’occupation soit visible immédiatement.

La programmation par objets fournit des outils pour réaliser de telles applications. Dans les cas les plus simples, elle ne diffère de la programmation impérative que par le changement de perspective qui fait passer les objets avant les actions. C’est une affaire de forme de pensée du programmeur; nombre d’entre eux restent attachés à la programmation impérative, qu’ils ont apprise en premier et dans laquelle ils s’expriment aisément. Pour les applications complexes, notamment sur réseaux, la programmation par objets est devenue le mode d’expression privilégié.

La programmation récursive

La programmation impérative se situe dans la perspective constructiviste des mathématiques, qui définit une fonction par la suite des opérations à effectuer pour la calculer. Elle s’opposait à la perspective intuitionniste, pour laquelle une définition implicite suffit à prouver l’existence d’une fonction. C’est la voie qu’inaugura John Mac Carthy, vers 1960, en créant le langage Lisp (List Processing Language). Elle se fonde elle aussi sur la récurrence, mais en l’exploitant d’une autre façon.

Reprenons l’ensemble du tri présenté plus haut. Nous sommes parti de l’idée qu’on mettait au bout, dans le bon ordre, les plus grands éléments, en sorte que l’on obtenait une partie triée, en place, au bout, et une partie en désordre, mais globalement en place, au début. Partant de:

on arrivait à:

Nous aurions pu dire qu’il ne restait plus qu’à trier la première partie. Il est inutile d’imaginer que la partie en place comporte plusieurs éléments. Il suffit d’en mettre un seul en place, le plus grand, et de trier le reste. Au XIX^e siècle, on a vivement reproché aux méthodes implicites de constituer des cercles vicieux: si on définit le tri à partir du tri, on met le mot à définir dans la définition, et on ne s’en sortira pas. Ce n’est pas exact, parce que l’on ramène le tri d’une suite à celui d’une suite plus courte, et qu’ainsi, de proche en proche, on finira par arriver à une suite d’un seul élément, toujours triée. D’où le programme:

Fondamentalement, ce programme dit que si l’on sait trier une suite de n – 1 éléments, on sait trier une suite de n éléments (on met le plus grand au bout, et on est ramené au cas de n – 1 éléments); or, on sait trier une suite de un élément, car elle est toujours triée, il n’y a rien à faire. Donc, on sait trier toutes les suites. C’est le type même du raisonnement par récurrence. Mais il y a économie de moyens: on ne dit pas comment se fait le tri, on dit seulement comment passer du tri de n – 1 éléments au tri de n .

En informatique, cette façon d’opérer est dite récursive plutôt qu’implicite: c’est le même concept qui est en jeu. Appliqué au cas du calcul d’une fonction, on aboutit à un résultat dont la véritable portée n’a pas été comprise tout de suite. Soit à obtenir la suite de caractères inverse d’une suite donnée, c’est-à-dire formée des mêmes caractères dans l’ordre inverse: l’inverse de NOEL est LEON. Le premier caractère de la suite donnée se retrouve en queue du résultat:

le reste de la donnée se trouve inversé en tête du résultat. Notons x :: y la mise bout à bout des suites x et y ; premier(s ), le premier caractère de la donnée s ; reste(s ), la suite s privée de son premier caractère. Notons inv(s ) l’inverse de s . Avec ces notations, dans le cas général, inv(s ) = inv(reste(s )):: premier(s ). Le processus s’arrête parce que reste(s ) est une chaîne plus courte que s , et qu’une suite vide (que nous notons nil) est son propre inverse. Notons longueur(s ) le nombre de caractères de s :

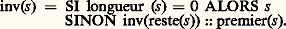
Ce programme ne comporte pas d’instruction d’affectation. Nous ne sommes plus dans un univers dynamique où les variables changent de valeur au cours du temps; nous sommes dans l’univers mathématique des fonctions implicites. Regardons comment cette définition fournit l’inverse de NOEL, chaîne de longueur 4:

On est ramené à l’inverse de OEL, de longueur 3:

Reportons ce résultat dans les lignes précédentes:

Le résultat est obtenu par un mécanisme complexe: on est renvoyé d’inverse en inverse sur des chaînes de plus en plus courtes, jusqu’à une chaîne vide dont on connaît l’inverse. On revient alors en arrière en construisant progressivement l’inverse.

La définition récursive nous dit que, dans le cas général, inv(reste(s )):: premier(s ). C’est une expression qui comporte une fonction inv mise bout à bout avec une autre chaîne, disons:

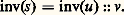
Prenons cela comme hypothèse de récurrence pour la construction d’un programme impératif. Si u est de longueur 0, alors inv(u ) = nil et inv(s ) = nil:: v = v . Sinon, inv(u ) = inv(reste(u )):: premier(u ), et donc:

Pour se ramener à la forme de récurrence, il faut changer premier(u ):: v en v , et reste(u ) en u . Pour démarrer, il faut mettre inv(s ) sous la forme inv(u ):: v , donc prendre u = s et trouver un v qui mis au bout de inv(s ) ne le modifie pas, donc prendre pour v une chaîne vide:

Nous constatons d’abord que nous avons pu construire un programme itératif en utilisant uniquement les informations fournies par la forme récursive. C’est un phénomène général: il y a des façons canoniques pour transformer un programme récursif en programme itératif. Interprétons le programme itératif obtenu: pour inverser la chaîne u en chaîne v , on enlève le caractère en tête de u , et on le met en tête de v . Le programme récursif dit qu’on peut inverser une chaîne. Le programme itératif dit comment le faire.

On peut dire que, en général, un programme récursif est plus simple à construire qu’un programme itératif pour qui maîtrise bien le raisonnement par récurrence ; que le programme itératif décrit la méthode de calcul, ce que ne fait pas le programme récursif; que le programme itératif est plus performant à l’exécution. Mais ce ne sont que des tendances générales; il arrive que le programme itératif soit plus simple que le récursif, que le récursif soit plus rapide. Le choix entre les deux modes de programmation est d’abord affaire de personne.

La programmation logique

Pour faire résoudre un problème par un ordinateur, il faut en fournir une méthode explicite de calcul si on utilise la programmation impérative, une méthode implicite par la programmation récursive. Dans les deux cas, il faut trouver une relation de récurrence exploitable. La programmation logique, inventée par le Français Alain Colmerauer, fait sortir de cet univers. Elle vise à donner à l’ordinateur non un algorithme de résolution, mais des informations sur les données et les relations qui les lient aux résultats. Un exemple donnera une idée de ce mode de programmation. Nous prendrons des libertés avec la syntaxe d’un quelconque langage logique, comme nous l’avons déjà fait pour les autres modes.

Je me propose d’étudier la généalogie d’une famille. Je vais considérer des relations comme «Jacques est père de Marie». Il faut généraliser: j’écrirai «X est-père Y», le trait d’union manifestant qu’il ne s’agit pas de mots de la langue française, mais du nom d’une relation entre X et Y. Cette relation est vraie si X est le père de Y, fausse sinon. On peut définir de nouvelles relations par composition:

à lire comme le fait que X est parent de Y si X est père de Y ou si X est mère de Y. La composition peut passer par une tierce personne:

Certaines relations peuvent n’avoir qu’une variable:

On peut alors définir est-frère:

(pour que X ne soit pas son propre frère). Voici une famille:

Demandons au système qui est grand-père de Jean:

Le système n’a qu’une seule règle concernant le grand-père: existence d’un Z tel que X soit père de Z, et Z parent de Jean. Le système cherche les parents de Jean et trouve Émile et Françoise. Il cherche le père d’Émile et trouve André, le père de Françoise et trouve Claude. Il répondra donc André et Claude. À la question Claude est-grand-père X, il va répondre en cherchant Z tel que: Claude est-père Z et Z est-parent X. Le seul Z tel que Claude est-père Z est Z = Françoise. Il n’y a pas de X tel que Françoise est-père X, mais il y a deux X tels que Françoise est-mère X: Jean et Lucie. Ainsi le système répond aussi bien à la question «qui est le grand-père de Jean?» qu’à la question «de qui Claude est-il grand-père?».

Nous sommes sortis du domaine où programmer veut dire trouver une méthode de résolution. Il n’y a plus création d’algorithme. On fixe les relations entre des éléments. On donne certains éléments, le système trouve tous ceux qui leur sont liés par ces relations. Pour y parvenir, l’ordinateur doit être muni d’un programme complexe qui cherche quelles règles appliquer et, au besoin, quelles variables supplémentaires mettre en jeu (Z dans l’exemple ci-dessus). Ce programme, appelé moteur d’inférence , relève des théories de la démonstration automatique.

Relation entre ces modes de programmation

Nous avons présenté les divers modes de programmation. En théorie, ils ont tous la même puissance d’expression. Mais ils ne relèvent pas de la même forme de pensée. La programmation impérative demande que l’on explicite la suite d’actions que devra faire l’ordinateur; c’est une œuvre de stratégie. Elle se fonde sur le couple situation-action, et sur la récurrence pour la création de boucles. La programmation récursive se fonde sur le concept de fonction et sur la récurrence pour la définition implicite de fonction. Elle est peut-être plus proche de la pensée mathématique. La programmation par objets met l’accent sur l’objet du traitement, les actions qu’il peut subir étant décrites impérativement ou récursivement. C’est la perspective qui est modifiée, pas la façon d’agir ou de définir. La programmation logique demande seulement une description formelle des relations entre données et résultats, mais ne peut éviter un recours aux définitions implicites.

Chaque mode a ses langages propres dont les plus connus sont Fortran, Cobol, Basic, C, Pascal, Ada pour la programmation impérative; Lisp, Logo pour la programmation récursive; Smalltalk, C++ pour la programmation objet; Prolog pour la programmation logique. Dans chaque famille, les langages sont construits sur les mêmes concepts. Ils diffèrent par la clarté de leurs structures, la richesse des constructions qu’ils permettent, la variété des objets qu’ils traitent. Mais ce sont des différences de surface, de sorte que, quand on connaît et maîtrise bien l’un d’eux, on passe assez facilement aux autres.

Un problème étant donné, il se peut qu’un des modes de programmation soit particulièrement adapté à sa résolution par un ordinateur. Seul celui qui connaît bien chacun des quatre modes brièvement présentés ci-dessus peut faire le bon choix. Le mode étant choisi, un certain langage peut être préférable parce qu’il a été spécialement conçu pour ce type de problème. On pourrait en déduire que le programmeur doit avoir une connaissance encyclopédique des modes et langages. Ce n’est fort heureusement pas indispensable. En théorie, tout peut être dit en n’importe quel mode avec un quelconque de ses langages. Le choix porte sur la facilité de construction du programme, sur la sécurité de son fonctionnement. Certains langages sont très largement diffusés, disponibles sur de nombreux types d’ordinateurs: ils permettront le transport facile d’une application d’un ordinateur à un autre. Le bon programmeur est à l’aise dans plusieurs modes et plusieurs langages: son travail en est facilité par le choix du plus approprié. Faute du bon choix, son travail sera plus long et plus pénible. L’important reste qu’il aboutisse.

• 1924; h. 1845; de programmer

1 ♦ Établissement, organisation des programmes (de cinéma, radio, télévision).

2 ♦ Élaboration et codification de la suite d'opérations formant un programme (4^o). ⇒aussi microprogrammation. Programmation de calculs. Programmation d'une machine électronique, d'une calculatrice (⇒ programmeur) . — Langage de programmation. Programmation structurée.

3 ♦ Fam. Action de prévoir et d'organiser (qqch.). Programmation des vacances. Programmation des naissances. ⇒ planification.

n. f.

d1./d Action de programmer (des films, des émissions).

d2./d INFORM établissement d'un programme.

|| Langage de programmation, utilisé pour programmer un traitement de l'information. (V. informatique.)

⇒PROGRAMMATION, subst. fém.

A. —SPECTACLES, CIN., RADIO, TÉLÉV. Établissement, organisation des programmes (de cinéma, radio, télévision); annonce de la présentation officielle d'un film. Un important circuit de salles constitue un groupement de programmation dont les membres s'engagent à passer des films d'une origine déterminée à des dates données (M. DE CARMOY, L'Industr. cin. (rapp. au Conseil nat. écon.), 1936, p.4):

• 1. Cette semaine appartient encore à Elizabeth II avec les reportages plus «travaillés» (...). À tort ou à raison, tout le reste de la programmation, dans la tradition policière ou réaliste se trouve effacé à l'arrière-plan.

Combat, 10 juin 1953, p.2, col. 4-5.

B. —ADMIN. Mode d'élaboration, définition d'un programme (économique, industriel, etc.). Programmation de logements dans les zones d'urbanisation. Recourir aux programmes (à la «programmation» comme dit le vrai «technicien») (PERROUX, Écon. XX^es., 1964, p.4). La programmation de l'enseignement supérieur et de la recherche (Loi orient. Enseign. sup., 1968, p.7).

— ÉCON., MATH. (appliquées à la gestion). Programmation linéaire. ,,Méthode de détermination de la valeur que doivent prendre différentes variables pour aboutir à une situation optimum, compte tenu de contraintes exprimées par des équations ou des inéquations`` (CIDA 1973). Quelque complexe que soit le traitement qu'on lui fasse subir, qu'il s'agisse de différenciation ou de programmation linéaire, ce traitement se ramène toujours à compter les unités ou à identifier les combinaisons qu'elles forment (JOLLEY, Trait. inform., 1968, p.227). La programmation est dite linéaire dans la mesure où toutes les variables sont du premier degré (BERN.-COLLI 1981). V. linéaire B 1 ex. de Hist. gén. sc.

C. —INFORMATIQUE

1. Ensemble des opérations permettant la conception, la réalisation, le test, la maintenance de programmes (d'apr. MORVAN Informat. 1981). Programmation en langage machine, en langage assembleur, en langage évolué. La programmation inclut les travaux d'écriture et de mise au point des programmes (LE GARFF 1975):

• 2. Le software se divise en deux branches: la première (...) recouvre les problèmes liés aux langages de programmation, la seconde (...) correspond aux systèmes d'exploitation.

J.-P. MEINADIER, Struct. et fonctionnement des ordinateurs, Paris, Larousse, 1971, p.14.

♦Langages de programmation. V. langage I B 2.

2. [Dans la lang. des journalistes] Synon. de software. La réalisation d'un gros calculateur est considérée par le groupe spécialisé comme un «projet» locomotive ayant un effet d'entraînement important (...) des composants, (...) des télécommunications et du software (programmation) (Le Monde, 4 juin 1969, p.11, col. 5).

Prononc.:[]. Étymol. et Hist. 1. 1921 «établissement d'un programme (de spectacle), inscription de quelque chose à un programme» (Cinémagazine, 25 nov., p.27a ds QUEM. DDL t.18); 2. 1959 informat. (P. DEMARNE, M. ROUQUEROL, Les Ordinateurs électron., Paris, P.U.F., p.111, note 1). Dér. de programme; suff. -ation, v. -tion. Corresp. à l'angl. programming «établissement d'un programme (en général)» (1889) et plus spéc. en informat. (1945) v. NED Suppl.². Bbg. DUB. Dér. 1962, p.32. —MÉNARD-LÉPINE (L.). Planning, programming et scheduling. Meta. 1980, t.25, pp.354-355. —QUEM. DDL t.6, 25.

programmation [pʀɔgʀamɑsjɔ̃] n. f.

ÉTYM. 1924, in D. D. L.; attestation isolée, 1845; de programmer.

❖

1 Établissement, organisation des programmes (cinéma, radio, télévision…). Distribution des copies d'un film aux salles de projection. — REM. Le mot ne se justifie qu'en langage de métier et lorsque programme(s) ne peut convenir. || Être chargé de la programmation. ⇒ Programmateur. || Service de programmation d'une entreprise de spectacles.