Akademik

CONIQUES

L’étude des coniques a été pendant deux millénaires le terrain de prédilection des géomètres qui ont accumulé sur ce sujet d’innombrables théorèmes. Dès la fin du III^e siècle avant J.-C., les mathématiciens avaient obtenu par des méthodes purement géométriques des résultats très complets: le Traité des sections coniques d’Apollonius (né vers 245 avant J.-C.) est un des sommets de la mathématique grecque (cf. école mathématique d’ALEXANDRIE).

Le XVII^e siècle allait voir à nouveau se développer la théorie des coniques dans deux directions très différentes. Descartes met en évidence les équations des coniques et reconnaît qu’elles constituent les courbes du second degré, tandis que Pascal et Desargues donnent une impulsion considérable à la géométrie pure en inaugurant l’étude projective des coniques ^{[cf. GÉOMÉTRIE]}.

De nos jours, les mathématiciens ne se préoccupent plus guère d’enrichir l’herbier un peu vieillot des théorèmes sur les coniques, qui ont été réduites à un chapitre de la théorie des formes quadratiques. Une conique apparaît aujourd’hui comme une courbe non vide du plan projectif, définie par une équation Q(x, y, t ) = 0, où Q est une forme quadratique en les coordonnées homogènes x, y, t ; cette définition est la seule qui contienne tous les cas particuliers et elle s’étend immédiatement en dimension supérieure aux quadriques et aux hyperquadriques.

On se limite dans ce qui suit à des résultats purement classiques, en renvoyant à l’article formes QUADRATIQUES pour un exposé plus moderne.

1. Les sections coniques

Le cône circulaire

Le cercle est la figure conique la plus simple et la plus ancienne; il a été considéré comme une figure bien avant le couple de droites, pourtant plus simple a priori (de tels couples existent dans toute géométrie, alors que le cercle n’apparaît que dans quelques-unes). On peut alors définir le cône circulaire, ensemble des droites s’appuyant sur un point fixe (le sommet O) et sur un cercle (la base C). Le plus simple de ces cônes est le cône de révolution, où la droite qui joint O au centre de C est perpendiculaire au plan du cercle.

Les sections d’un cône circulaire par un plan sont appelées sections coniques. On peut ainsi obtenir, outre le cercle, des ellipses, des paraboles, des hyperboles et des figures particulières (droites sécantes si le plan passe par le sommet, droites confondues s’il contient de plus une tangente au cercle). Seul échappe à cette définition (conforme à l’étymologie) le cas de deux droites parallèles distinctes. Celui-ci pourra néanmoins venir compléter la famille en application du théorème: Toute section plane d’un cône dont une base est une conique est elle-même une conique ou le plan tout entier.

Ce théorème capital, qui va beaucoup plus loin que la définition grecque (qui ne considérait que certains types de cônes), affirme en quelque sorte que la notion de conique est la notion projective fondamentale, c’est-à-dire la notion invariante dans toute perspective par excellence, si l’on consent naturellement à étudier, dans le plan ou l’espace projectifs, autre chose que des configurations exclusivement formées de droites.

Dans le plan projectif où la notion de droites parallèles ne se différencie pas de celle de droites sécantes (en un point à l’infini), les ellipses, hyperboles et paraboles sont de même nature: ce sont des coniques propres. Deux droites distinctes, deux droites confondues forment les deux sous-familles de coniques décomposées.

Un théorème de Pascal

Citons maintenant un important résultat projectif, le célèbre théorème de Pascal: si A, B, C, D, E, F sont six points d’une conique (décomposée ou non), les points d’intersection de BF et CE, AF et CD, AE et BD sont alignés. Cela permet une construction point par point à partir de cinq points d’une conique. Elle provient de ce que le point d’intersection de deux droites passant par des points fixes dont les pentes sont liées homographiquement décrit une conique; cette définition, très élémentaire, est peut-être la meilleure de toutes et ramène très simplement à la définition analytique par une forme quadratique. Elle explique, par sa simplicité, pourquoi des coniques interviennent si souvent dans les problèmes élémentaires de géométrie pure ou de mécanique.

Coniques décomposées

Historiquement, c’est pourtant par des considérations affines et surtout métriques que les coniques ont été reconnues et étudiées. Dans un plan métrique tel que le plan euclidien traditionnel, les cas particuliers de coniques décomposées sont triviaux et on ne les considérera plus dans le cadre de cet article. Il suffira de dire que deux droites sécantes forment le cas de décomposition d’une hyperbole, deux droites parallèles (ou même confondues) celui d’une parabole ; nous en tenant ici aux coniques réelles, il est clair qu’une ellipse ne peut se décomposer en droites dans notre système volontairement limité.

Restent les trois grands types: ellipse (dont le cercle est un cas particulier capital), hyperbole (pour laquelle l’hyperbole équilatère joue un rôle analogue), parabole.

2. La parabole

Définitions

La parabole est la plus simple des trois coniques traditionnelles (cercle mis à part, naturellement: on ne le considérera ici que comme un cas particulier d’ellipse). La notion de parabole est affine, non métrique; c’est-à-dire qu’il suffit de choisir, parmi les droites d’un plan projectif, une tangente à une conique pour en faire la droite de l’infini: la conique en question devient alors une parabole. Par contre, les concepts d’axe, de sommet, de foyer surtout, étant métriques, nous donnerons de la parabole des définitions équivalentes plus élémentaires que celle qui la décrit comme une «conique tangente à la droite de l’infini», utilisant les longueurs (ou, ce qui est équivalent, la notion de cercle).

Étant donné une droite D, appelée directrice, et un point F (le foyer) non situé sur elle, la parabole est:

– l’ensemble des points M qui sont centre d’un cercle passant par F et tangent à la droite D (définition 1);

– l’ensemble des points M tels que la distance MF soit égale à la distance MH de M à la droite D (définition 2).

La perpendiculaire à D issue de F est l’axe de la parabole. Si elle coupe la directrice en un point K, la distance FK = p est le paramètre de la parabole. Le sommet S, situé sur la courbe, est le milieu de KF; la médiatrice de KF est d’ailleurs la tangente au sommet. Toute la courbe est connexe, convexe et symétrique par rapport à l’axe (fig. 1).

Tangentes

En chaque point M de la parabole, il existe une tangente. Celle-ci est bissectrice de l’angle formé par MF et la parallèle à l’axe; cette bissectrice rencontre l’axe en un point T tel que S soit milieu de la projection sur l’axe du segment MT: cela détermine entièrement la tangente en M (fig. 1). La formule coupe l’axe en un point N tel que les vecteurs KFet MNaient des projections de même valeur sur l’axe: l’invariance de la projection de MN est une propriété caractéristique de la parabole.

Tout point d’une parabole pouvant être pris comme sommet si l’on modifie convenablement la condition d’orthogonalité dans le plan, certaines des propriétés précédentes sont en fait affines et non réellement métriques. Prenons par exemple une parallèle quelconque (H) à l’axe. Elle coupe la parabole en un point unique Z où la tangente sera notée (V): on constate alors que la parabole est invariante dans la symétrie par rapport à (H) parallèlement à (V), et que Z est le milieu de la projection de la partie de tangente à la parabole comprise entre son point de contact et (H) [fig. 2]. (H) est appelé diamètre de la direction de (V), c’est-à-dire ensemble des milieux des segments PQ parallèles à (V) dont les extrémités sont sur la parabole; les tangentes en P et Q se coupent d’ailleurs sur (H). La démonstration de ces propositions peut se ramener à une simple projection d’une parabole sur un autre plan, Z étant alors l’image du sommet, (H) celle de l’axe, etc.

Le dénombrement des points d’intersection d’une droite avec une parabole, la partition du plan en «extérieur» et «intérieur» sont naturellement des notions affines. On se bornera pourtant, pour la commodité, à considérer une parabole métrique, la projection signalée ci-dessus permettant l’extension de ces notions à une parabole affine.

Intersection avec une droite

Une droite coupe une parabole en un ou deux points. Si le point d’intersection est unique et la droite non parallèle à l’axe, la droite est tangente. Pour qu’il en soit ainsi, il faut et il suffit que la projection du foyer F sur elle appartienne à la tangente au sommet, ce qui donne une définition traditionnelle de la parabole comme enveloppe de droites (dont la projection sur elles d’un point fixe décrit une droite fixe). Le point de contact est alors aisément déterminé par sa projection sur l’axe, symétrique de T par rapport à S. Il existe une tangente unique ayant une direction donnée, sauf si celle-ci est celle de l’axe. Si une tangente variable coupe deux tangentes fixes distinctes en U et U , les abscisses de ces points sont liées par une relation affine (x = ax + b ), ce qui est une propriété affine, et le triangle UFU reste semblable à lui-même (ses angles sont constants), ce qui est une propriété métrique; toutes deux sont caractéristiques de la parabole. Si les tangentes fixes se coupent en V, F appartient au cercle (UVU ) et l’orthocentre du triangle UVU est sur la directrice.

Donnons-nous une droite quelconque D. Si la projection de F sur D est sur la tangente au sommet, on vient de voir que D est une tangente à la parabole. Si cette projection est du même côté de cette tangente au sommet que F, D coupe effectivement la parabole en deux points distincts (un seul si D est parallèle à l’axe) que l’on peut construire à la règle et au compas (suivant les vieilles règles grecques). Si cette projection est située dans l’autre demi-plan, il n’existe aucun point d’intersection.

Prenant le problème d’un point de vue différent, on peut chercher les tangentes à la parabole issues d’un point donné M. Il en existe une seule si M est sur la courbe. Sinon MF 礪 MH définit l’extérieur de la parabole, d’où l’on peut mener deux tangentes à la courbe (perpendiculaires si M appartient à la directrice); de l’intérieur, caractérisé par MF 麗 MH, on ne peut mener de tangentes. Le foyer est à l’intérieur.

Propriétés différentielles et intégrales

Par un point donné, il peut exister jusqu’à trois normales à la parabole, coupant celle-ci en trois points définissant un cercle passant par le sommet, et un triangle dont le centre de gravité appartient à l’axe.

Le centre de courbure C en M, point où la normale en M est tangente à son enveloppe, se projette en P sur MF de façon que FM = FP = FN (N étant l’intersection de la normale et de l’axe); CM = R est le rayon de courbure, lié à MF par l’égalité p R² = 8M³. La normale CNM coupe la directrice en D tel que CM= 2MD 轢.

L’aire comprise entre un arc de parabole SM, l’axe et la projetante de M sur l’axe est égale aux deux tiers de l’aire du rectangle de diagonale SM, de côtés parallèles et perpendiculaires à l’axe (une telle propriété se conserve, mutatis mutandis , par projection). Cette quadrature, la première du genre, était déjà connue d’Archimède qui utilisait là sa méthode d’exhaustion. Des géomètres tels que Roberval retrouvèrent ce résultat par des raisonnements inspirés de la mécanique et du fait que la portion de tangente comprise entre M et l’axe était coupée en son milieu par sa tangente au sommet: ils obtenaient ainsi deux arcs symétriques de paraboles découpant trois aires égales dans un rectangle (fig. 3).

La plupart des propriétés de la parabole sont évidemment généralisables aux autres coniques, dites coniques à centre; pour certaines d’entre elles, la parabole apparaît en quelque sorte comme un moyen terme entre l’ellipse et l’hyperbole. Mais la parabole garde son originalité: par exemple, ce qui est rare pour une conique autre qu’un cercle, la parabole est rectifiable, ce qui veut dire que l’on peut donner une formule explicite pour la longueur d’un arc de parabole SM. Dans un système d’axes orthogonaux d’origine S dont l’axe des abscisses est l’axe de la parabole, si t est un nombre tel qu’abscisse et ordonnée de M soient égales respectivement à:

alors la longueur de l’arc SM est:

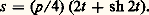
Les longueurs des arcs des autres coniques ne peuvent s’exprimer en général qu’à l’aide de fonctions elliptiques.

3. Les coniques à centre

Foyers

Pour les coniques à centre, les deux définitions métriques courantes sont les suivantes:

– l’ensemble des points M qui sont centre d’un cercle passant par un point donné F et tangent à un cercle donné C de centre F : définition bifocale (fig. 4);

– l’ensemble des points M tels que la distance MF soit proportionnelle à la distance MH de M à la droite D (directrice associée à F): définition monofocale.

La première met en jeu deux foyers, F et F , et le cercle directeur C de centre F et de rayon (2a ). Par hypothèse, FF = 2c est distinct de 2a (F n’appartient pas à C ). Si l’on peut écrire c 麗 a , alors F est intérieur à C et la courbe obtenue, lieu de M tel que:

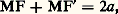
est une ellipse, convexe, connexe et bornée (fig. 5). Si c 礪 a , F est extérieur à C : l’hyperbole obtenue est composée de deux parties convexes et connexes respectivement définies par MF 漣 MF = 2a et MF 漣 MF = 2a . Pour un cercle, c = 0.

Ces coniques admettent deux axes de symétrie perpendiculaires (dont FF , appelé axe focal) et un centre de symétrie O, milieu de FF . L’axe focal coupe la courbe aux sommets A et A , tels que:

Une ellipse a deux autres sommets B et B sur l’axe secondaire de symétrie, définis par OB = OB = b avec

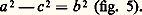
Pour une hyperbole, on pose au contraire: c ² 漣 a ² = b ², si l’on veut n’utiliser que des nombres réels.

Tangentes

En chaque point d’une conique à centre il existe une tangente. Celle-ci est la bissectrice de l’angle géométrique FMF (extérieure pour l’ellipse, fig. 6, intérieure pour l’hyperbole). On ne peut mener deux tangentes MT et MT distinctes à la conique que par un point M extérieur à celle-ci, défini par exemple par la relation MF 礪 e MH, où e = c /a est l’excentricité de la conique (inférieure à 1 pour l’ellipse, égale à 1 pour la parabole par définition, et supérieure à 1 pour l’hyperbole). Sur la conique même (MF = e MH), ce qui est la seconde définition, il y a une tangente unique (double). D’un point intérieur (MF 麗 e MH) on ne peut pas mener de tangentes; c’est notamment le cas en F ou en F . Si les tangentes existent, MT et MT ont mêmes bissectrices que MF et MF ; de plus FM est bissectrice de l’angle TFT (cf. fig. 7, pour l’ellipse). MT est perpendiculaire à MT si M appartient au cercle de Monge, de centre O et de rayon 連2a ² 漣 c ² (pour e 諒 連2).

La projection de F sur une tangente décrit le cercle de diamètre AA ; si la projection de F sur une droite est dans la même région que F par rapport à ce cercle, la droite donnée coupe la conique en deux points distincts que l’on peut construire; si la projection est dans l’autre région, la droite ne coupe pas la conique. On peut déduire de cela des définitions de l’ellipse et de l’hyperbole comme enveloppes de droites, comme pour la parabole.

Parmi les tangentes à une hyperbole, deux sont particulières. Issues de O, elles n’ont aucun point de contact à distance finie avec la courbe dont elles sont des asymptotes; elles déterminent deux angles contenant chacun une branche connexe de l’hyperbole.

Correspondances linéaires

Si une tangente variable coupe deux tangentes fixes à une conique à centre, les abscisses x et x des deux points d’intersection sont reliées par une relation homographique du type:

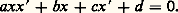
Il existe une réciproque importante à cette propriété affine: une droite joignant deux points de deux droites fixes dont les abscisses sont reliées par une telle relation (où a 0) enveloppe une conique à centre (a = 0 correspond à une parabole). Le produit des distances des deux foyers à une tangente variable est égale à b ²; les foyers sont de part et d’autre pour une hyperbole, du même côté pour une ellipse. Certaines des propriétés précédentes s’étendent naturellement à une parabole, en supposant par exemple que la direction de F est celle de l’axe.

Pour que quatre points d’une conique soient sur un même cercle, il faut et il suffit que deux des cordes les joignant soient symétriques par rapport aux axes de la conique. D’un point du plan, on peut mener jusqu’à quatre normales à une conique à centre. Les pieds de trois d’entre elles et le point diamétralement opposé au quatrième sont sur un même cercle.

Si l’on se donne deux directions perpendiculaires, les points d’où les tangentes issues ont des directions symétriques par rapport à ces directions privilégiées appartiennent à une hyperbole (équilatère) de même centre que la conique, passant par les deux foyers; il en serait de même si l’on remplaçait les deux directions choisies par celles de leurs bissectrices, d’où la position des foyers à l’intersection des deux hyperboles.

Propriétés différentielles et intégrales

La normale en M coupe l’axe focal en N tel que NF = e MF. La perpendiculaire en N à MN coupe MF en P, projection du centre de courbure C en M sur MF, et coupe MO en Q, point tel que QC soit perpendiculaire à l’axe focal (fig. 8): cela fournit deux constructions du centre de courbure, sauf aux sommets de l’axe focal où le rayon de courbure R = MC est égal à p = b ²/a , paramètre de la conique (et longueur de la demi-corde issue de F et perpendiculaire à FF ). En un point quelconque, on a:

On retrouve aussi le paramètre comme longueur de la projection orthogonale de MN sur MF ou MF . Si N est sur la médiatrice de FF et sur MN, MN se projette suivant une longueur égale à a sur MF ou MF , et les trois vecteurs N N 轢, N Met NMsont proportionnels aux nombres c ², a ² et a ² 漣 c ² (b ² pour une ellipse, 漣 b ² pour une hyperbole).

Les centres de courbure en les sommets A et B d’une ellipse sont alignés avec le point d’intersection des tangentes en A et B; cette droite est perpendiculaire à AB; la construction des cercles de courbure en A et B permet une construction graphique très soignée de l’arc AB.

Pôles et polaires

Si une corde MM coupe la directrice D en

P, FP est une bissectrice de l’angle MFM . Si MM passe par F, les tangentes en M et en M se coupent en T sur la directrice, et P est conjugé harmonique de F par rapport

à M et M ; de plus l’angle MFT est droit. Cette directrice D est située à une distance a ²/c de O, est perpendiculaire à l’axe focal et située du même côté de O que F. Elle n’existe pas pour un cercle pour lequel F, F et O sont confondus, d’où c = e = 0; cela fait que la définition monofocale, qui masque déjà le caractère de double symétrie de la conique, n’est pas aussi générale qu’elle paraît. Il existe naturellement une directrice analogue D pour l’autre foyer F .

Pour une conique propre quelconque, à centre ou parabole, les conjugués harmoniques d’un point fixe M par rapport aux extrémités P et Q d’une corde passant par M sont situés sur une droite, appelée polaire de M (fig. 9). Ainsi une directrice est la polaire du foyer correspondant. Seul le centre n’a pas de polaire. Un point de la conique a sa tangente comme polaire. Toute droite ne passant pas par le centre éventuel est la polaire d’un certain point qui est appelé son pôle.

Si la polaire de M passe par M , celle de M passe par M. Si M, P, Q sont alignés, leurs polaires sont concourantes et réciproquement. Si MT et MT sont des tangentes issues de M, la corde TT qui joint leurs points de contact est la polaire de M (cf. fig. 9 pour l’ellipse). Ces propriétés peuvent être obtenues très simplement par perspective (conique éventuellement) à partir des propriétés analogues pour le cercle, où elles sont bien connues; elles sont projectives en dépit des apparences.

Diamètres

Donnons-nous une direction D; les milieux des cordes parallèles à D sont situés sur un

diamètre, c’est-à-dire une droite passant par le centre (ellipse ou hyperbole) ou parallèle à l’axe (parabole). La conique est invariante dans la symétrie par rapport à ce diamètre parallèlement à la direction D. Fixons un point M; à tout diamètre de direction D, associons son point d’intersection avec la perpendiculaire issue de M au diamètre conjugué de D défini ci-dessus. Ces points engendrent une hyperbole (équilatère), coupant la conique aux points où la normale passe par M, ce qui permet de les construire.

Pour une ellipse, à tout diamètre D, on peut associer le diamètre conjugué D dont D est à nouveau le conjugué. D et D coupent l’ellipse en P et Q, par exemple, tels que la tangente en P soit parallèle à D , et forme avec D, D et la tangente en Q, un parallélogramme d’aire constante, égale à ab , comme on le voit en prenant les axes de l’ellipse pour D et D (fig. 10). De plus OP² + OQ² = a ² + b ² est constant. De tels diamètres conjugués sont simplement les projections orthogonales de deux diamètres perpendiculaires d’un cercle de diamètre AA placé de façon que l’ellipse soit sa projection: la plupart des propriétés de la conjugaison (ainsi que la formule donnant l’aire de l’ellipse: S = 神ab ) sont des conséquences immédiates de cette projection.

4. Propriétés particulières

L’ellipse

Une construction très simple permet d’obtenir autant de points de l’ellipse que l’on en désire. Donnons-nous deux droites perpendiculaires Ox et Oy , et un segment constant PQ dont les extrémités décrivent respectivement Ox et Oy (fig. 11). Un point M situé entre P et Q tel que MQ = a et MP = b décrit une ellipse de centre O, d’axe focal Ox . La tangente en M est perpendiculaire à IM, où I est le quatrième sommet d’un rectangle OPIQ. Deux positions perpendiculaires de PQ (appelé «bande de papier» dans la littérature) correspondent à deux extrémités de diamètres conjugués. I décrit le cercle de centre O et de rayon (a + b ); le symétrique J de I par rapport à M est lui aussi sur la normale en M; il décrit le cercle de centre O et de rayon (a 漣 b ), et Ox est bissectrice intérieure de l’angle IOJ; IJFF sont sur un même cercle, et forment la figure connue sous le nom de quadrangle harmonique, inverse d’une division harmonique (fig. 11).

La projection considérée, que l’on peut relier à l’affinité d’axe AA et de rapport b /a , qui transforme le cercle de diamètre AA en l’ellipse, est à l’origine d’une représentation paramétrique particulièrement simple de celle-ci. Le transformé du point du cercle définissant, avec Ox , un angle t est en effet le point de l’ellipse de coordonnées x = a cos t , y = b sin t ; t est l’anomalie excentrique de ce point. Deux extrémités de diamètres conjugués, dont les pentes dans ce système d’axes ont pour produit b ²/a ², ont des anomalies excentriques différentes d’un angle droit. L’équation de l’ellipse en découle; on pourrait aussi la déduire des formules d’Euler, valables également pour une hyperbole:

pourvu que F soit le point de coordonnées (c , 0). Cette équation s’écrit:

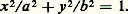
L’ellipse intervient notamment en astronomie. Tout point attiré par un autre point F suivant la loi de Newton décrit une conique de foyer F. Les planètes, qui ont un mouvement périodique, décrivent des ellipses, seules coniques à être bornées. L’aire comprise entre la courbe et les droites joignant F à deux positions du point mobile est proportionnelle à l’intervalle de temps séparant les deux positions; pour une planète, la période T du mouvement est telle que ² soit proportionnel au cube a ³ de la longueur:

ce sont les fameuses lois de Kepler.

L’hyperbole

L’hyperbole, à cause de ses asymptotes, possède des propriétés très particulières. Il n’existe pas nécessairement de tangentes ayant une direction donnée (il suffit de considérer des droites passant par le centre et situées dans les deux angles déterminés par les asymptotes où sont situées les deux branches). L’angle de ces asymptotes est l’angle 2z défini par cos z = 1/e . Les points d’intersection avec les tangentes en A et A sont les sommets d’un rectangle de côtés 2a et 2b .

Cette dernière propriété se généralise de la façon suivante. Considérons un diamètre P OP de l’hyperbole. La droite passant par O et parallèle à la tangente en P est le diamètre conjugué de la direction OP. Il ne coupe pas l’hyperbole. Mais si l’on y construit le point Q tel que OP² 漣 OQ² = a ² 漣 b ², l’aire du triangle OPQ est constante (et vaut ab /2); quand P varie, Q décrit une autre hyperbole, dite conjuguée de la précédente, ayant même centre et mêmes asymptotes, échangeant a et b avec la précédente (fig. 12). De plus, la tangente en Qy est parallèle à OP, et coupe la tangente en P sur une asymptote. Enfin la conjuguée de la conjuguée est l’hyperbole originale. Les deux diamètres «conjugués» OP et OQ forment un faisceau harmonique avec les asymptotes. La symétrie par rapport à OP et parallèlement à OQ laisse invariante chacune des deux hyperboles conjuguées.

Revenant à une hyperbole simple, la famille de ses tangentes jouit d’une propriété remarquable (due au fait que les asymptotes sont des tangentes très particulières); partant du fait qu’une corde MM coupe les asymptotes en des points P et P tels que l’on ait MP= P M 轢, la tangente en M coupe les asymptotes en Q et Q tels que M soit le milieu de QQ . QQ FF sont situés sur un même cercle et forment un quadrangle harmonique. De plus, si une droite passant par M coupe les asymptotes en P et P et se déplace parallèlement à elle-même, le produit MP . MP reste constant: il est notamment égal à b ² si MPP est perpendiculaire à l’axe focal.

L’hyperbole équilatère

Parmi toutes les hyperboles, l’hyperbole équilatère, d’excentricité 連2 (a = b ), est particulièrement intéressante. Ses asymptotes sont perpendiculaires.

Considérons les sommets A et A , le cercle de diamètre AA , un point P décrivant ce cercle (fig. 13). Menons par A la droite symétrique de AP par rapport à la direction de AA ; cette droite coupe A P en M, point de la branche contenant A de l’hyperbole équilatère de sommets A et A . Le triangle AMA est pseudo-rectangle, c’est-à-dire que la différence des angles en A et A est égale à un droit. La tangente en M au cercle (AMA ) est perpendiculaire à AA , qu’elle coupe en H tel que HM² = HA . HA (comme dans un véritable triangle rectangle). Si A PM coupe la tangente au sommet A en le point T, conjugué harmonique de A par rapport à M et P, les tangentes en P (au cercle) et en M (à l’hyperbole) se coupent sur AT au milieu de ce segment; elles coupent AA en les projections de P et de M; M se projette sur AT en un point appartenant à OP, etc. (fig. 13). Cette figure est la base de la correspondance entre les trigonométries circulaire et hyperbolique; elle inspira à Abraham de Moivre sa fameuse formule:

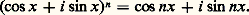
Si l’aire comprise entre OA, OM et l’hyperbole est égale à a ²t /2, les coordonnées de M (dans les axes convenables) sont alors x = a ch t, y = a sh t , d’où l’équation x ² 漣 y ² = a ². Toute hyperbole étant affine d’une hyperbole équilatère de même sommet, l’équation générale d’une hyperbole est donc:

et celle des asymptotes est obtenue en y remplaçant 1 par 0. La fonction «gudermanien de t », utilisée pour construire les cartes géographiques selon la projection de Mercator, est définie par:

a ²/2.t est la moitié de l’aire comprise entre OA, OP et le cercle.

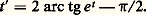
Dans une hyperbole équilatère:

le rayon de courbure R est tel que a ²R = OM³. Si C et C sont deux points de l’hyperbole symétriques par rapport à O, les bissectrices de CMC sont parallèles aux asymptotes, et la différence des angles C et C est constante. Tout cercle passant par CC est recoupé suivant un diamètre; un cercle de centre C et de rayon CC recoupe l’hyperbole équilatère suivant les sommets d’un triangle équilatéral. Deux hyperboles équilatères se coupant en les sommets et l’orthocentre d’un triangle, on peut en déduire de nombreuses propriétés. Si une corde MM se déplace en restant parallèle à elle-même, en coupant toujours l’hyperbole, le cercle de diamètre MM passe par deux points fixes où la normale est parallèle à MM .