- морфизм алгебраич. многообразий, удовлетворяющий условиям: 
для всех 
и g, 
(е- единица G). Если 
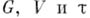определены над полем k, то 
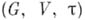наз. алгебраич. группой k-преобразований. Напр., 
- присоединенное действие или действие посредством сдвигов, является А. г. п. Если G - алгебраич. подгруппа в GL(n), 
- ее естественное действие в аффинном пространстве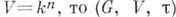 
- А. г. п. Для всякой точки 
через 
обозначается орбита х, а через 
- стабилизатор х. Орбита 
не обязательно замкнута в V, но всегда существуют замкнутые орбиты, напр, замкнутые орбиты минимальной размерности. Иногда под А. г. п. понимается алгебраич. группа G, действующая рационально (но не обязательно регулярно) на алгебраич. многообразии V(это значит, что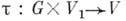 
- рациональное отображение, а выписанные выше свойства т выполнены для общих точек). Как показал А. Вейль [3], всегда существует многообразие 
бирационально изоморфное Vи такое, что действие 
индуцированное рациональным действием Gна V, регулярно. Задачи описания орбит, стабилизаторов, полей инвариантных рациональных функций (см. Инвариантов теория).и построения фактормногообразий являются основными в теории А. г. п. и имеют многочисленные применения. Лит.: [1]Борель А., Линейные алгебраические группы, пер. с англ., М., 1972; [2] Дьедонне Ж., Керрол Д ж., Мамфорд Д., Гее метрическая теория инвариантов, пер. с англ., М., 1974; [3] Well A., "Amer. J. Math.", 1955, v. 77, Ms 2, p. 355-91. В. П. Платонов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.