Akademik

(от лат. fluctuatio - колебание) - случайные отклонения физ. величин от их средних значений. Ф. испытывают любые величины, зависящие от случайных факторов. Количественные характеристики Ф. основаны на методах матем. статистики и теории вероятностей. Простейшей мерой Ф. случайной величины х служит её дисперсия 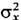, т. е. ср. квадрат отклонения х от ср. значения х, 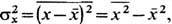где черта сверху означает статистич. усреднение. Эквивалентной мерой Ф. является среднеквадратичное отклонение 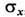, равное корню квадратному из дисперсии, или его относит, величина 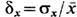. Взаимное влияние Ф. неск. величин х_i определяется их корреляциями 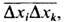где 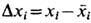. Для статистически независимых величин 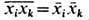и, следовательно, корреляции равны нулю (см. также Корреляционная функция в статистич. физике).

В статистич. физике Ф. вызываются хаотическим тепловым движением частиц, образующих систему. Даже в состоянии статистич. равновесия наблюдаемые физ. величины испытывают Ф. около ср. значений. С помощью Гиббса распределений как в классическом, так и в квантовом случае можно вычислить равновесные Ф. для систем, находящихся в разл. внеш. условиях; при этом Ф. выражаются через равновесные термодинамич. параметры и производные потенциалов термодинамических. Напр., для системы с пост, объёмом V и пост, числом частиц N, находящейся в контакте с термостатом (с темп-рой T), каноническое распределение даёт для Ф. энергии 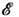результат: 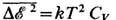где C_V - теплоёмкость системы при пост, объёме. В приведённом примере флуктуирует т. н. экстенсивная (пропорц. объёму) физ. величина - энергия. Её относит, квадратичные Ф. 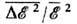пропорциональны 1/N, т. е. очень малы. Равновесные Ф. др. экстенсивных величин (объёма, числа частиц, энтропии и т. д.) ведут себя с ро-

стом числа частиц аналогичным образом. T. о., в состоянии статистич. равновесия макроскопич. величины с очень большой точностью равны своим ср. значениям Однако для выделенных малых объёмов Ф. могут быть легко обнаружены (особенно вблизи критических точек), напр., по рассеянию света, рентг. лучей или медленных нейтронов.

Для детальной характеристики Ф. вводится функция распределения их вероятностей (см. также Статистическая физика). Если флуктуирующая величина х описывает состояние системы в целом или к.-л. её макроскопич. части, то неравновесное состояние системы, связанное с появлением Ф., можно рассматривать как неполное статистич. равновесие с заданным значением рассматриваемой величины. Для изолированной системы вероятность w(x)dx величине х иметь значение в интервале между х и x + dx пропорциональна соответствующему статистич. весу, а ф-ция распределения равна w(x) = Cexp{S(x)/k}, где S (х) - энтропия неполного равновесия, характеризуемого точным значением флуктуирующей величины. Постоянная С находится из условия нормировки ф-ции распределения. Для неск. флуктуирующих макроскопич. величин Xi равновесная ф-ция распределения Ф. имеет вид

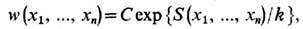
где энтропия рассматривается как ф-ция точных значений всех флуктуирующих величин. Приведённая ф-ла для ф-ции распределения Ф. макроскопич. величин является основой т. н. термодинамической теории флуктуации, впервые сформулированной А. Эйнштейном (1910). T. к. относительные Ф. макроскопич. величин малы, то энтропия 5 (x₁, ..., х_n )может быть разложена в ряд по степеням отклонений 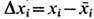. С точностью до членов 2-го порядка по этим отклонениям равновесная ф-ция распределения макроскопич. величин совпадает с Гаусса распределением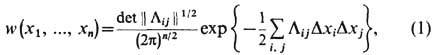

где 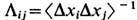-матрица, обратная корреляционной матрице, 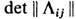-её определитель. Для Ф. термодинамич. величин подсистемы, к-рая находится в равновесии с остальными частями изолир. системы (термостатом), ф-ла (1) даёт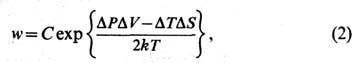

где 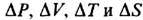-изменения давления, объёма, темп-ры и энтропии подсистемы при Ф., T- темп-pa термостата. Выбирая в ф-ле (2) в качестве независимых переменных разл. параметры подсистемы, можно вычислить все характеристики равновесных термодинамич. Ф.

Вблизи критических точек жидкостей и растворов, а также вблизи точек фазовых переходов наблюдается аномальный рост Ф. нек-рых физ. величин (параметров порядка) и их взаимодействие. Для чистых жидкостей параметрами порядка являются плотности массы и энергии, для растворов - концентрации компонент, для ферромагнетиков в окрестности Кюри точки - намагниченность и т. д. Рост Ф. приводит к ряду аномалий в поведении термодинамич. величин и в реакции системы на внеш. воздействие (критические явления).

Существует связь между Ф. физ. величин в равновесном состоянии и линейными диссипативными процессами, вызванными как внеш. механич. возмущениями (электропроводность, реакция на внешнее переменное магн. поле), так и внутр. неоднородностями в системе (напр., диффузия, теплопроводность и вязкость). Соотношения, связывающие характеристики линейных диссипативных процессов (проводимость, магн. восприимчивость, коэффициенты диффузии, теплопроводности, вязкости и т. д.) с пространственно-временными корреляционными ф-циями 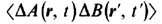флуктуирующих динамич. переменных, наз. флуктуационно-диссипативными теоремами. К флук-

туационно-диссипативным теоремам относятся Кубо формулы для тензоров электропроводности и магн. восприимчивости и Трина - Кубо формулы для коэф. переноса. Флук-туационно-диссипативные теоремы для общего случая были сформулированы X. Кэлленом (H. В. Callen) и T. Уэлтоном (Th. A. Welton) в 1951 как обобщение Най-квиста формулы для электрич. шумов в линейных цепях; они оказываются полезными для вычисления спектральной плотности временных корреляционных ф-ций равновесных Ф. в тех случаях, когда обобщённые восприимчивости удаётся вычислить с помощью Грина функций (в статис-гич. физике) или к.-л. др. методом.

Ур-ния, описывающие эволюцию неравновесной макро-скопич. системы, напр, кинетическое уравнение Больцмана для классич. газа или ур-ния гидродинамики, являются ур-ниями для физ. величин, усреднённых по статистич. ансамблю. Вследствие теплового движения в системе эти величины испытывают Ф. около ср. значений.

Кинетические Ф. в газе характеризуются корреляц. ф-пией 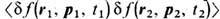, где 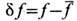является отклонением точной, микроскопич. ф-ции распределения f от ср. значения этой ф-ции 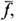определяемого кинетич. ур-нием. В равновесном газе корреляц. ф-ция зависит только от разности времен t₁ - t₂ и разности координат r₁-r₂, а 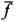есть независящая от времени равновесная одночастич-ная ф-ция распределения. В частности, если нет внеш. поля, эта ф-ция совпадает с Максвелла распределением f₀(p).

Вычисление корреляц. ф-ции для кинетич. Ф. в равновесном газе можно свести к решению обобщённого Ланжевена уравнения

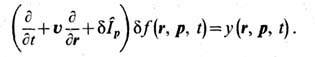
Левая часть этого ур-ния совпадает с линеаризов. кинетич. ур-нием Больцмана, где 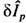-линейный интегральный оператор (оператор столкновений), а правая часть представляет собой случайный источник, моменты к-рого определяются соотношениями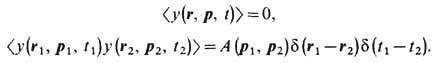

Интенсивность источника, описывающего влияние теплового движения частиц на Ф. одночастичной ф-ции распределения, имеет вид

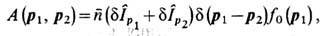
где 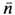-равновесная концентрация частиц. Метод Ланжеве-на применим и к исследованию кинетич. Ф. в неравновесном газе, однако выражение для второго момента случайного источника является значительно более сложным. Кинетич. Ф. в квантовых газах описываются ур-ниями Ланжевена для отклонений одночастичной матрицы плотности или одночастичной Вигнера функции распределения от ср. значений, определяемых квантовым кинетич. ур-нием.

Для крупномасштабных гидродинамич. Ф. в газах и жидкостях применимо понятие локального (частичного) равновесия в малых объёмах при фиксиров. значениях флуктуирующих термодинамич. параметров. Поэтому в гидродинамич. пределе, когда длина волны Ф. велика по сравнению с микроскопич. размерами (межатомным расстоянием в жидкости и длиной пробега в газе), вычисление временных корреляц. ф-ций Ф. плотности, темп-ры, скорости и т. д. сводится к решению гидродинамич. ур-ний с дополнительными ланжевеновскими источниками, описывающими тепловой шум. Метод вычисления корреляц. ф-ций крупномасштабных Ф. в равновесном состоянии, основанный на линейных ур-ниях гидродинамики со случайными источниками, был предложен Л. Д. Ландау и E. M. Лифшицем в 1957. В случае однокомпонентной классич. жидкости тензор вязких напряжений тт,, и вектор потока тепла q записываются в виде

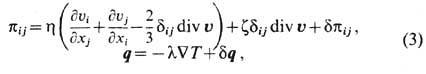
где 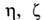-коэф. вязкости, 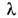-коэф. теплопроводности. Кроме обычных членов с градиентами скорости и градиентом темп-ры, эти выражения содержат ланжевенов-ские источник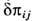и и 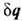; они описывают спонтанные напряжения и потоки тепла, вызванные тепловым движением частиц.

Статистич. свойства источников в приближении локального термодинамического равновесия могут быть установлены методами термодинамики неравновесных процессов.Cp. значения источников равны нулю, а вторые моменты даются ф-лами

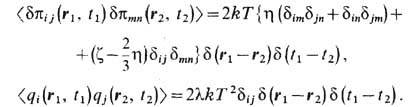
Решив систему линеаризованных гидродинамич. ур-ний, в к-рых тензор вязких напряжений и вектор потока тепла имеют вид (3), можно выразить временные корреляционные ф-ции Ф. локальных гидродинамич. переменных 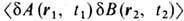через равновесные термодинамич. величины и коэффициенты переноса. В частности, таким способом можно вычислить корреляц. ф-цию Ф. плотности числа частиц 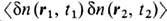, через к-рую выражается динамический структурный фактор жидкости, измеряемый в экспериментах по рассеянию света и медленных нейтронов.

Нелинейное взаимодействие гидродинамич. Ф. необходимо учитывать вблизи критич. точки, где сильный рост равновесных крупномасштабных Ф. приводит к аномалиям наблюдаемых коэффициентов переноса, а также в неравновесных состояниях, когда система теряет гидродинамич. устойчивость. Характерными примерами являются конвективная неустойчивость и возникновение турбулентности в жидкостях и газах. Взаимодействие крупномасштабных Ф. описывается нелинейными членами в ур-ниях гидродинамики, где локальные термодинамич. величины рассматриваются как случайные переменные.

Лит.: Ландау Л. Д., Лифшиц E. M., Статистическая физика, ч. 1, 3 изд., M., 1976; Зубарев Д. H., Неравновесная статистическая термодинамика, M., 1971; Паташинский А. 3., Покровский В. Л., Флуктуационная теория фазовых переходов, 2 изд., M., 1982; Климонтович Ю. Л., Статистическая физика, M., 1982; Лифшиц E. M., Питаевский Л. П., Статистическая физика, ч. 2, M., 1978; Форстер Д., Гидродинамические флуктуации, нарушенная симметрия и корреляционные функции, пер. с англ., M., 1980. В. Г. Морозов.