Akademik

СЕЧЕНИЕ

СЕЧЕНИЕ: (эффективное сечение), величина, характеризующая вероятность перехода системы двух сталкивающихся ч-ц в результате их рассеяния (упругого или неупругого) в определённое конечное состояние. С. s равно отношению числа dN таких переходов в ед. времени к плотности nv потока рассеиваемых ч-ц, падающих на мишень, т. е. к числу ч-ц, проходящих в ед. времени через единичную площадку, перпендикулярную к их скорости v (n — плотность числа падающих ч-ц): a=dN/nv. Т. о., С. имеет размерность площади. Разл. типам переходов, наблюдаемых при рассеянии ч-ц, соответствуют разные С. Упругое рассеяние ч-ц характеризуют дифференциальным сечением ds/dW, равным отношению числа ч-ц, упруго рассеянных в ед. времени в ед. телесного угла, к потоку падающих ч-ц (dW— элемент телесного угла), и полным сечением s, равным интегралу дифф. сечения, взятому по полному телесному углу W=4p стер. На рис. схематически изображён процесс упругого рассеяния точечных «классич.» ч-ц на шарике радиуса R0 с «абсолютно жёсткой» поверхностью; полное С. рассеяния равно геом. сечению шарика: s=pR20.

При наличии неупругих процессов полное С. складывается из С. упругих и неупругих процессов. Для более детальной хар-ки рассеяния вводят С. для отд. типов (каналов) неупругих реакций. Для множественных процессов важное значение имеют т. н. инклюзивные сечения, описывающие вероятность появления в данном столкновении к.-л. определённой ч-цы или группы ч-ц.

Если вз-ствие между сталкивающимися ч-цами велико и быстро падает с увеличением расстояния, то С. по порядку величины, как правило, равно квадрату радиуса действия сил или геом. сечению системы (см. рис.);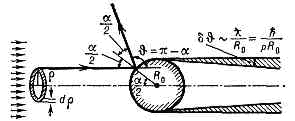

Схема, поясняющая упругое рассеяние «классич.» ч-цы на «абсолютно твёрдом» шарике. Рассеянию на угол q=p-a отвечает прицельный параметр r=R0sin(a/2)=R0cos(q/2), а сечение ds рассеяния в телесный угол dW=2psinqdq равно площади заштрихованного кольца: ds=2prdr=(p/2)R20sinqidq, т. е. дифф. сечение ds/dW=R20/4, а полное сечение упругого рассеяния равно геом. сечению шарика: s=pR20. При учёте квант. (волн.) св-в ч-ц сечение получается иным. В предельном случае l->R0 (l=ћ/р — длина волны де Бройля ч-цы, р — её импульс) рассеяние сферически симметрично, а полное сечение в 4 раза больше классического: sкв=4pR20. При l-R0 рассеяние на конечные углы (q?0) напоминает классическое, однако под очень малыми углами dq=l/R0 происходит волновое «дифракц.» рассеяние с сечением pR20; т. о., полное сечение с учётом дифракции вдвое больше классического: s=2pR20. однако вследствие специфич. квантовомеханич. явлений С. могут существенно отличаться от этих значений (напр., в случаях резонансного рассеяния и Рамзауэра эффекта).

Эксперим. измерения С. рассеяния дают сведения о структуре сталкивающихся ч-ц. Так, измерения сечения упругого рассеяния a-частиц атомами позволили открыть ат. ядро, а упругого рассеяния эл-нов нуклонами — определить радиусы нуклонов и распределение в них электрич. заряда и магн. момента (т. н. эл.-магн. формфакторы). Понятие «С.» используется также в кинетич. ур-ниях, описывающих неравновесные процессы в статистич. физике.

СЕЧЕНИЕ

(эффективное сечение) - величина, характеризующая вероятностьперехода системы двух сталкивающихся частиц в результате их рассеяния (упругогоили неупругого) в определённое конечное состояние. С.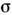равно отношению числа dN таких переходов в единицу времени к плотности nv потока рассеиваемых частиц, падающих на мишень, т. е. к числучастиц, проходящих в единицу времени через единичную площадку, перпендикулярнуюк их скорости v (п - плотность числа падающих частиц): 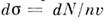Т. о., С. имеет размерность площади. Разл. типам переходов, наблюдаемыхпри рассеянии частиц, соответствуют разные С. Упругое рассеяние частицхарактеризуют дифференциальным сечением , равным отношению числа частиц, упруго рассеянных в единицу телесногоугла, к потоку падающих частиц (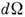- элемент телесного угла), и полным упругим сечением 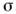,равным интегралу дифференциального сечения, взятому по полному телесномууглу. На рис. схематически изображён процесс упругого рассеяния точечных«классич.» частиц на шарике радиуса R₀ с «абсолютно жёсткой»поверхностью; полное С. рассеяния равно геом. сечению шарика: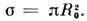

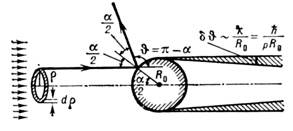
Схема, поясняющая упругое рассеяние «классической» частицы на «абсолютнотвёрдом» шарике. Рассеянию на угол 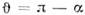отвечает прицельный параметр 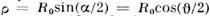, сечение 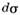рассеяния в телесный угол 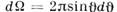равно площади заштрихованного кольца: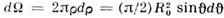,т. е. дифференциальное сечение 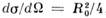, а полное сечение упругого рассеяния равно геом. сечению шарика: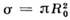.При учёте квантовых (волновых) свойств частиц сечение получается иным. В предельном случае 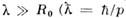- длина волны де Бройля частицы, р - её импульс) рассеяние сферически симметрично, а полное сечение в 4 раза больше классического: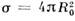При 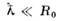рассеяниена конечные углы 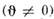напоминает классическое, однако под очень малыми углами 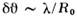происходит волновое «дифракционное» рассеяние с сечением 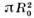;т. о., полное сечение с учётом дифракции вдвое больше классического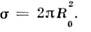

При наличии неупругих процессов полное С. складывается из С. упругихи неупругих процессов. Для более детальной характеристики рассеяния вводятС. для втд. типов (каналов) неупругих реакций. Для множественных процессов важное значение имеют т. н. инклюзивные сечения, описывающие вероятностьпоявления в данном столкновении к.-л. определ. частицы или группы частиц.

Если взаимодействие между сталкивающимися частицами велико и быстропадает с увеличением расстояния, то С. по порядку величины, как правило, равно квадрату радиуса действия сил или геом. сечению системы; однако вследствиеспецифич. квантовомеханич. явлений С. могут весьма существенно отличатьсяот этих значений (напр., в случаях резонансного рассеяния и Рамзауэраэффекта).

Эксперим. измерения С. рассеяния дают сведения о структуре сталкивающихсячастиц. Так, измерения угл. зависимости С. упругого рассеяния a-частицатомами позволили открыть атомное ядро, а С. упругого рассеяния электроновнуклонами - определить радиусы нуклонов и распределение в них электрич. заряда и магн. момента (т. н. эл.-магн. формфакторы). Изучение С. глубоко неупругих процессов рассеяния лептонов на нуклонах обнаружилосоставляющие их «точечные» частицы достаточно малых размеров - партоны.

В квантовой теории С. равно квадрату модуля амплитуды рассеяния. Полное С. рассеяния связано с мнимой частью амплитуды упругого рассеянияна нулевой угол оптической теоремой.

Понятие С. используется также в кинетич. ур-ниях, описывающих неравновесныепроцессы в статистич. физике. С. С. Герштейн. СЖАТИЕ - см.Растяжение.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.